1.2 Системи лінійних рівнянь

Завдання 1.2

1. Методом Крамера знайти розв’язання системи лінійних алгебраїчних рівнянь.

2. Встановити, що система рівнянь має єдиний розв’язок, і знайти його за допомогою оберненої матриці.

3. Методом Гауса (або методом виключення невідомих) знайти розв’язання системи лінійних алгебраїчних рівнянь.

4. Знайти загальний розв'язок однорідної системи лінійних алгебраїчних рівнянь.

5. При яких значеннях система рівнянь має нетривіальні (ненульові) розв’язки? Знайти ці розв’язки.

Зразок розв’язання.

1. Методом Крамера знайти розв’язок системи лінійних алгебраїчних рівнянь.

.

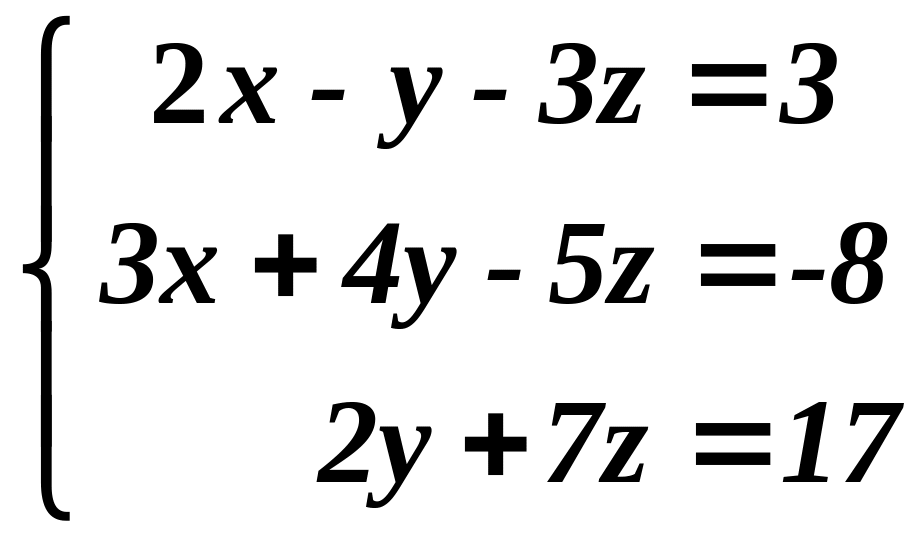Розв’язання.

Розв’язок системи знаходимо за формулами Крамера

.

Обчислимо визначник системи

.

Послідовно замінивши в , перший, другий і третій стовпці стовпцями вільних членів, одержимо відповідно

;

;

.

Відповідь: .

2. Задана система з трьох рівнянь з трьома невідомими. Встановити, що система рівнянь має єдиний розв’язок, і знайти його за допомогою оберненої матриці.

.

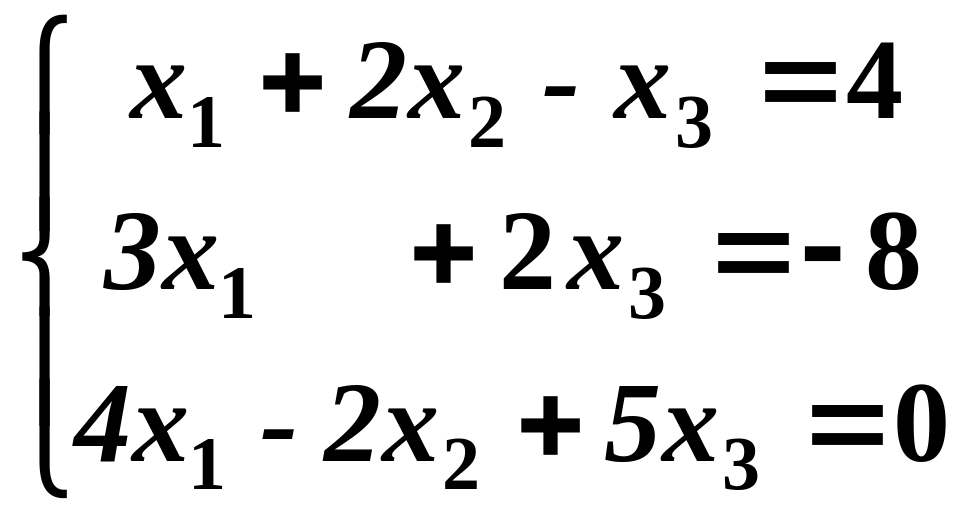Розв’язання.

Якщо визначник системи відмінний від нуля, то система має єдиний розв’язок (теорема Крамера).

Обчислимо визначник даної системи:

,

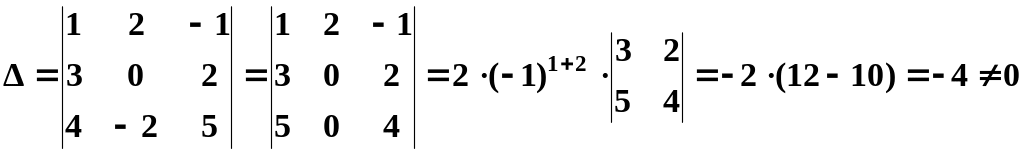отже, система має єдиний розв’язок.

Дану систему можна записати у матричній формі:

, де , , .

Оскільки , то для матриці існує обернена матриця . Помноживши матричне рівняння ліворуч на , отримаєм , звідки , або .

Знайдем обернену матрицю за формулою

,

де алгебраїчне доповнення елемента .

,

,

.

.

Тоді

.

Відповідь: .

3. Методом Гауса (або методом виключення невідомих) знайти розв’язання системи лінійних алгебраїчних рівнянь.

.

Розв’язання.

Напишемо розширену матрицю даної системи і зведемо її до східчастого виду

.

Послідовно помножимо перший рядок на (-2) і додаємо його до другого рядка, потім помножимо на (-3) і додаємо до третьому рядка, помножимо на (-2) і додаємо до четвертого рядка, отримаємо

.

До другого рядка отриманої матриці додаємо третій рядок, помножений на , потім у знов отриманій матриці помножимо третій рядок на , четвертий - на , потім послідовно помножимо другий рядок на 2 і додаємо його до третього рядка, помножимо на 7 і додаємо до четвертого рядка, отримаємо

.

Третій рядок отриманої матриці помножимо на , четвертий – на , потім третій рядок помножимо на і додаємо до четвертого рядка, отримаємо

.

Одержана матриця має трикутний вид; за цією матрицею запишемо систему рівнянь, еквівалентну початковій системі,

.

Послідовно знаходим невідомі, починаючи з останнього рівняння, ; підставимо до третього рівняння знайдене , обчислимо , ; потім з другого рівняння знаходим , ; з першого рівняння одержимо , .

Відповідь: .

4. Знайти загальний розв'язок однорідної системи лінійних алгебраїчних рівнянь.

.

Розв’язання.

Елементарними перетвореннями рядків зведемо матрицю системи до еквівалентної матриці , якій відповідає рівняння , еквівалентне вихідній системі. Таким чином, загальний розв’язок може бути записаний у формі , або , . Розв’язків нескінченна множина - будь-яка пара, пов'язана зазначеною залежністю, перетворює ліві частини рівнянь даної системи в нуль. У системі - число невідомих і число рівнянь. , матриця системи, розширена матриця системи. За теоремою Кронекера-Капеллі система має незліченну кількість роз в’язків, що залежать від одного параметра . Іноді загальний розв’язок зручніше використовувати в формі

.

5. При яких значеннях система

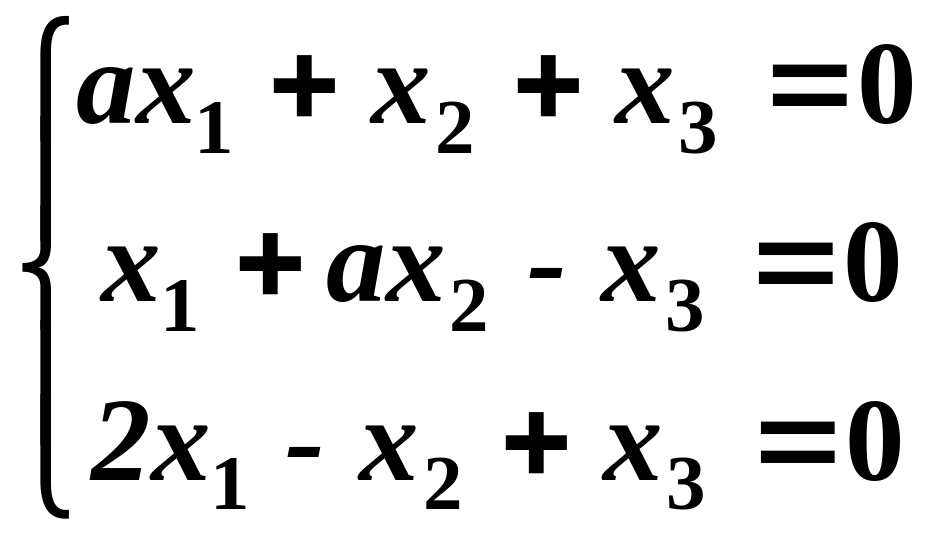
має нетривіальні (ненульові) розв’язки ? Знайти ці розв’язки.

Розв’язання.

Однорідна система лінійних рівнянь має ненульові розвозки, коли її визначник дорівнює нулю. З цієї умови і знайдемо відповідні значення :

.

Знайдем тепер відповідні розв’язки.

1) При система має вид :

.

Визначник цієї системи дорівнює нулю. Це означає наявність лінійної залежності між рівняннями системи. Відмічаємо, що перше рівняння виходить з другого і тому його можна відкинути. Маємо

.

Оскільки визначник з коефіцієнтів при невідомих не дорівнює нулю, то в якості базисних змінних візьмемо (можна брати й інші пари змінних) і перенесемо члени з до правої частини рівнянь:

.

Одержану систему можна розв’язати за формулами Крамера :

де , , .

Тоді , . Вважаючи, що , де довільне дійсне число, одержимо розв’язок системи: , , .

2) При система має вид :

.

Можна розв’язати цю систему і методом Гаусса. Складемо розширену матрицю отриманої системи :

і зведемо її до матриці східчастого виду:

.

Відновимо систему для отриманої матриці

.

Вважаючи, що , де довільне дійсне число, отримуємо розв’язок системи: .

Відповідь : При система має нетривіальний розв’язок : , , , . При система має нетривіальний розв’язок: , .