Розрахунково-графічна робота №1 лінійна алгебра

1.1 Матриці і визначники

Завдання 1.1.

1. Обчислити визначник 3-го порядку, використовуючи метод Саррюса (або метод трикутників) і метод розкладання за мінорами для довільного ряду.

2. Обчислити визначник вищого порядку.

3. Привести матрицю до ступінчастого вигляду і обчислити ранг матриці.

4. Виконати дії з матрицями.

5. Обчислити значення многочлена від матриці .

6. Знайти невідому матрицю з рівняння

Зразок розв’язання

1.Обчисліть визначник 3-го порядку:

1) за правилом Саррюса (або правило трикутників). Це правило полягає в наступній рівності:

.

Таким чином,

2) Друге правило обчислення називається розкладанням за елементами довільного рядка (або стовпця). Наприклад, розкладання за елементами першого рядка має вигляд:

.

Визначник

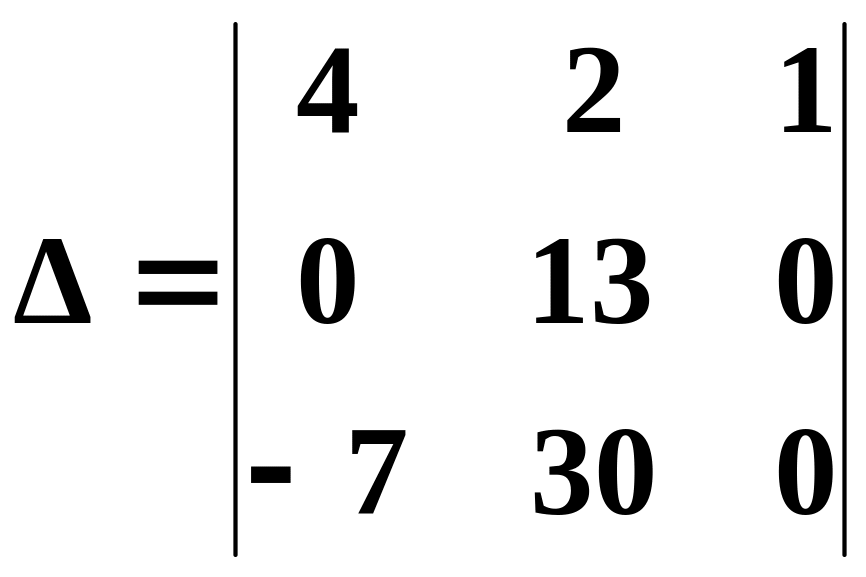
Розкладемо за елементами третього стовпця, тобто

.

Як видно з наведених прикладів, обчислення визначників значно спрощується, якщо ряд визначника має тільки один елемент, відмінний від нуля. Цього можна завжди досягти, використовуючи властивості визначників. У визначнику

помножимо перший рядок на 2 і додаємо до другого, додаємо перший рядок до третього, отримаємо

.

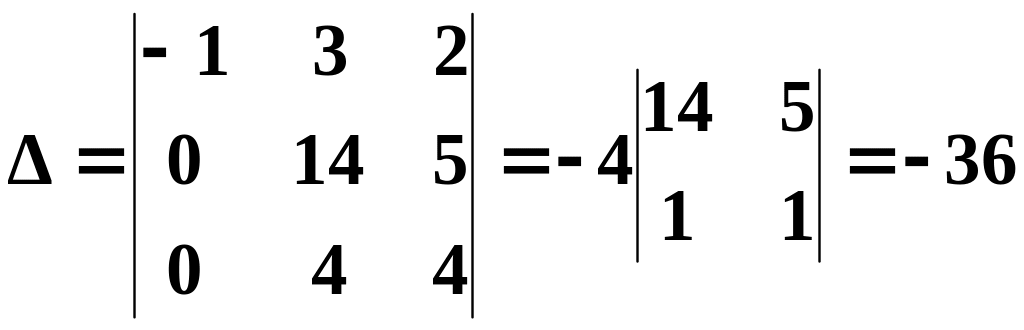2. Обчислити визначник вищого порядку

.

Розв’язання:

Використовуючи властивості визначника, знизимо порядок визначника. З цією метою додаємо п'ятий стовпець до першого:

;

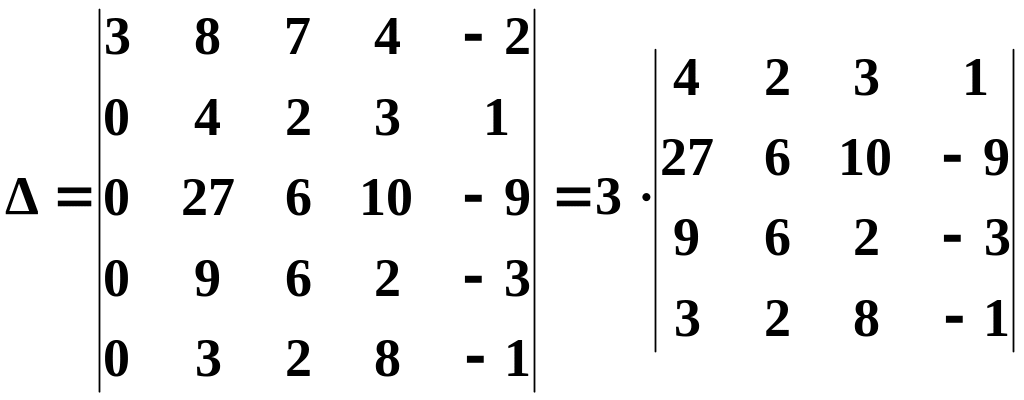в отриманому визначнику 4-го порядку четвертий стовпець помножимо на 3 і додаєм до першого стовпця, потім помножимо його на 2 і додаєм до другого стовпця, помножимо його на 8 і додаємо до третього стовпця, отримуємо

.

З наведеного прикладу зрозуміло, що обчислення визначників вищих порядків значно спрощується, якщо визначник привести до трикутного вигляду.

3. Привести матрицю до ступінчастого вигляду і обчислити ранг матриці

.

Розв’язання.

Говорять, що квадратна матриця має східчастий вигляд, якщо нижче її головної діагоналі стоять нульові елементи. Матриця приводиться до східчастого виду і за допомогою елементарних перетворень:

а) перестановка рядків,

б) множення рядка на число,

в) додавання до одного рядка іншого, помноженого на деяке число. Ранг матриці , , дорівнює кількості ненульових рядків еквівалентної їй матриці східчастого виду.

У першому стовпці цієї матриці нижче першого елемента отримаємо нульові елементи за допомогою перетворення в). Послідовно помножимо перший рядок матриці на (-2) і додаємо до другого рядка, помножимо на (-3) і додаємо до третього рядка, помножимо на (-2) і додаємо до четвертого рядка, отримаємо

.

Щоб отримати нулі в матриці до другої рядку додаємо третій рядок, помножений на (-1), результат напишемо на місці другого рядка. Далі, поділимо третій рядок на (-2), четвертий рядок на (-1), маємо

.

У другому стовпці отриманої матриці нижче другого елементу отримаємо нульові елементи. Послідовно помножимо другий рядок отриманої матриці на 2 і додаємо до третьому рядку, помножимо на 7 і додаємо до четвертого рядку, потім третій рядок поділимо на 9, четвертий рядок поділимо на 18. У новоствореній матриці в третьому стовпці нижче третього елемента отримаємо нульовий елемент: третій рядок помножимо на (-1) і додаємо до четвертого рядку, маємо

.

Звідки, .