
- •Тема 3. Информационно-логические основы построения эвм лекция 3.2. Представление информации в эвм
- •Представление символьной информации
- •ФорМы записи чисел
- •2.1. Естественная форма
- •2.2. Нормальная форма
- •Форматы Представления чисел
- •3.1. Формат с фиксированной точкой
- •3.2. Формат с плавающей точкой
- •3.3. Двоично-десятичный код
- •Выполнение арифметических операций с числами с фиксированной и плавающей запятой
- •4.1. Действия над числами, представленными в естественной форме (с фиксированной запятой)
- •4.2. Действия над числами, представленными в нормальной форме (c плавающей запятой)
Тема 3. Информационно-логические основы построения эвм лекция 3.2. Представление информации в эвм
Представление символьной информации
Поскольку байт имеет 256 различных состояний, то с помощью 1 байта можно закодировать 256 различных символов. Состояние байта (числа от 0 до 25510 или 0 до 3778, или от 0 до FF16) при этом будет представлять код одного из символов. Как мы уже отмечали наиболее распространенным двоичным кодом как для передачи по каналам связи, так и для представления символов в ЭВМ является код ASCII (American Standard Code for Information Interchange - Американский стандартный код для обмена информацией).
Для возможности кодировки русского текста используется его расширение до 8 битов (КОИ-8). Полная таблица кода разбита на 16 строк и 16 столбцов, имеющих 16-ричные номера от 0 до F. Код символа составляется из номера столбца, к которому приписывается номер строки. Основной стандарт для кодирования символов использует шестнадцатеричные коды 00-7F, расширение стандарта – 80-FF. Основной стандарт является международным и используется для кодирования управляющих символов, цифр и букв латинского алфавита; в расширении стандарта кодируются символы псевдографики и буквы национального алфавита (естественно, в разных странах разные).
ФорМы записи чисел
В ЭВМ применяются две формы представления двоичных чисел:
естественная форма или форма с фиксированной запятой (точкой);
нормальная форма или форма с плавающей запятой (точкой).
2.1. Естественная форма
С фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
Пример 3.12. В десятичной системе счисления имеются 5 разрядов в целой части числа (до запятой) и 5 разрядов в дробной части числа (после запятой); числа, записанные в такую разрядную сетку, имеют вид:
+00721,35500; +00000,00328; -10301,20260.
Достоинствами этой формы являются простота, естественность, наглядность представления чисел, простота алгоритмов реализации арифметических операций и выполняющих их устройств, а, следовательно, высокая скорость выполнения операций. Но она имеет существенный недостаток – небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях.
Пример 3.13. Диапазон значащих чисел (Q) в системе счисления с основанием m при наличии L разрядов в целой части и k разрядов в дробной части числа (без учета знака числа) будет:
m-k ≤ Qm≤ ml – m-k.
При
m=2,
l=10
и k
= 6:
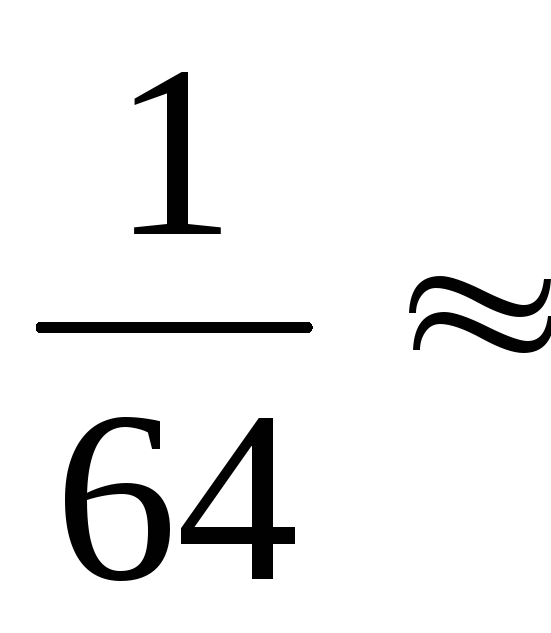 0,015
≤Q
≤ 1024.
0,015
≤Q
≤ 1024.
В современных ЭВМ естественная форма представления используется как вспомогательная и только для целых чисел, при этом запятая строго устанавливается после младшего разряда.
2.2. Нормальная форма
В нормальной форме (её называют также полулогарифмической, экспоненциальной или с плавающей запятой, положение которой определяется порядком) каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком. В общем виде число в форме с плавающей запятой может быть представлено так:
Qm = ±M×m±p, (3.12)
где М – мантисса числа (|М| < 1); p – порядок числа (p – целое число); m – основание системы счисления.
Для однозначности представления чисел используется нормализованная форма, при которой абсолютная величина мантиссы должна отвечать условию:
1/m ≤ |M| < 1
Ограничение справа требует, чтобы мантисса представлялась правильной дробью, ограничение слева — чтобы после запятой присутствовала значащая цифра (не 0).
Пример 3.14. Приведенные в примере 3.12 числа в нормальной форме запишутся так:
+0,721355×103; +0,328×10-3; -0,103012026×105.
Нормальная форма представления имеет огромный диапазон отображения чисел и является основной в современных ЭВМ.
Пример 3.15. Диапазон значащих чисел в системе счисления с основанием m при наличии n разрядов у мантиссы и k разрядов у порядка (без учета знаковых разрядов порядка и мантиссы) будет:
![]() ,
,
где pmax=mk-1. При m=2, n=10 и k=6 диапазон чисел простирается примерно от 10-22 (2-10 2-63 = 2-10 × (2-10)6 × 2-3≈ 10-3 × (10-3)6×10 -1) до 1019 ((1 – 2-10 )×263 ≈ (210)6 ×23 ≈ (103)6×10).
