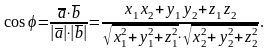- •Режим доступа к электронному аналогу печатного издания: http://www.Libdb.Sssu.Ru
- •Содержание
- •Предисловие
- •1 Линейная алгебра Краткий теоретический материал
- •1.1 Матрицы
- •1.2 Определители
- •1.3 Понятие алгебраического дополнения
- •1.4 Обратная матрица
- •1.5 Ранг матрицы
- •1.6 Системы линейных алгебраических уравнений
- •Лабораторная работа 1 действия над матрицами
- •Пример выполнения лабораторной работы
- •Лабораторная работа №2 вычисление ранга матрицы и нахождение обратной матрицы
- •Пример выполнения лабораторной работы
- •Лабораторная работа 3 решение систем линейных уравнений
- •Лабораторная работа 4 решение задач линейной алгебры
- •Задания
- •Варианты заданий
- •Пример выполнения работы № 1
- •Контрольные вопросы
- •2. Элементы векторной алгебры
- •2.1 Векторы
- •2.2 Скалярное произведение и его свойства
- •2.3 Векторное произведение векторов
- •Свойства векторного произведения
- •2.4 Смешанное произведение векторов
- •3. Элементы аналитической геометрии
- •3.1 Прямая на плоскости
- •3.2 Плоскость в пространстве
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
Контрольные вопросы
Что называется матрицей размера ?
Какая матрица называется квадратной, нулевой, единичной?
Какие операции можно выполнять с матрицами? Свойства матричных операций.
Что понимают под элементарными преобразованиями матрицы?
Что называется определителем 2-го, 3-го порядков? Сформулируйте свойства определителей.
Что такое миноры матрицы? Что называется алгебраическим дополнением элементов квадратной матрицы?
Какая матрица называется невырожденной?
Дайте определение обратной матрицы. Всякая ли матрица имеет обратную?
Какие методы нахождения обратной матрицы Вы знаете?
Что называется рангом матрицы?
Какие методы вычисления ранга матрицы Вы знаете?
Что называется системой линейных алгебраических уравнений (СЛАУ)?
Что называется решением СЛАУ?
Какая СЛАУ называется совместной, несовместной? Сформулируйте теорему Кронекера-Капелли.
Какие методы решения СЛАУ Вы знаете? В чём они заключаются?
Сформулируйте теорему о числе решений СЛАУ.
Как найти решение матричного уравнения XA=B ?
2. Элементы векторной алгебры
2.1 Векторы
Вектором
называется
направленный
прямолинейный отрезок, т.е. отрезок,
имеющий определенную длину и определенное
направление. Если
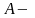 начало
вектора, а
начало
вектора, а
 его
конец, то вектор обозначается символом
его
конец, то вектор обозначается символом
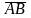 .
Символом
.
Символом
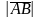 будем обозначать длину вектора
.
Вектор, длина которого равна нулю,
называется нулевым вектором и обозначается
будем обозначать длину вектора
.
Вектор, длина которого равна нулю,
называется нулевым вектором и обозначается
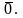 Нулевой вектор направления не имеет.
Вектор, длина которого равна единице,
называется единичным вектором. Векторы
Нулевой вектор направления не имеет.
Вектор, длина которого равна единице,
называется единичным вектором. Векторы
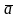 и
и
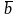 называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых; записывают
.
Два вектора
и
называются равными, если они одинаково
направлены и имеют одинаковые длины.
Три вектора в пространстве называются
компланарными, если они лежат в одной
плоскости или в параллельных плоскостях.
называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых; записывают
.
Два вектора
и
называются равными, если они одинаково
направлены и имеют одинаковые длины.
Три вектора в пространстве называются
компланарными, если они лежат в одной
плоскости или в параллельных плоскостях.
Пусть
в пространстве задана прямоугольная
декартова система координат
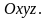 Выделим в пространстве единичные векторы
(орты), обозначаемые
Выделим в пространстве единичные векторы
(орты), обозначаемые
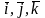 ,
имеющие такие же направления как и
координатные оси
,
имеющие такие же направления как и
координатные оси
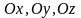 соответственно. Любой вектор
можно представить в виде линейной
комбинации векторов
:
соответственно. Любой вектор
можно представить в виде линейной
комбинации векторов
:
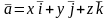 .
В этом случае говорят, что вектор
имеет координаты
.
В этом случае говорят, что вектор
имеет координаты
 в базисе
.
Если известны координаты точек
в базисе
.
Если известны координаты точек
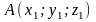 и
и
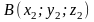 ,
то координаты вектора
равны разностям соответствующих
координат его конца и начала:
,
то координаты вектора
равны разностям соответствующих
координат его конца и начала:
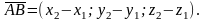 Длину вектора
можно найти по формуле
Длину вектора
можно найти по формуле
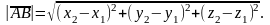
Если
векторы
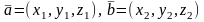 ,
то
,
то
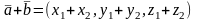 и
и
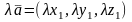 при любом действительном
.
при любом действительном
.
2.2 Скалярное произведение и его свойства
Скалярным
произведением двух ненулевых векторов
и
называется число, равное произведению
длин этих векторов на косинус угла между
ними. Обозначается
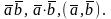 Итак, по определению
Итак, по определению
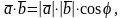 где
где
 (4)
(4)
Если
хотя бы один из векторов
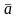 или
равен
или
равен
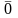 ,
то скалярное произведение полагается
равным 0.
,
то скалярное произведение полагается
равным 0.
Свойства скалярного произведения:
1)
 переместительный
закон.
переместительный
закон.
2)
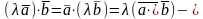 сочетательное
свойство относительно скалярного
множителя
сочетательное
свойство относительно скалярного
множителя

3)
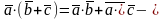 распределительный
закон.
распределительный
закон.
4)
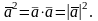
5) Для того чтобы ненулевые векторы и были взаимно перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
6)
Если векторы
и
заданы координатами:
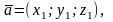
 то
то
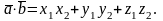
Из
формулы (4) найдем