- •Режим доступа к электронному аналогу печатного издания: http://www.Libdb.Sssu.Ru
- •Содержание
- •Предисловие
- •1 Линейная алгебра Краткий теоретический материал
- •1.1 Матрицы
- •1.2 Определители
- •1.3 Понятие алгебраического дополнения
- •1.4 Обратная матрица
- •1.5 Ранг матрицы
- •1.6 Системы линейных алгебраических уравнений
- •Лабораторная работа 1 действия над матрицами
- •Пример выполнения лабораторной работы
- •Лабораторная работа №2 вычисление ранга матрицы и нахождение обратной матрицы
- •Пример выполнения лабораторной работы
- •Лабораторная работа 3 решение систем линейных уравнений
- •Лабораторная работа 4 решение задач линейной алгебры
- •Задания
- •Варианты заданий
- •Пример выполнения работы № 1
- •Контрольные вопросы
- •2. Элементы векторной алгебры
- •2.1 Векторы
- •2.2 Скалярное произведение и его свойства
- •2.3 Векторное произведение векторов
- •Свойства векторного произведения
- •2.4 Смешанное произведение векторов
- •3. Элементы аналитической геометрии
- •3.1 Прямая на плоскости
- •3.2 Плоскость в пространстве
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
Пример выполнения лабораторной работы
1)
Даны координаты вершин треугольника: ,
,
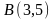 ,
,
 .
.
a) Введём формулу для нахождения уравнения прямой по двум точкам, задав пользовательскую функцию up:
>up:=(x,x1,x2,y,y1,y2)->(x-x1)/(x2-x1)-(y-y1)/(y2-y1)=0;
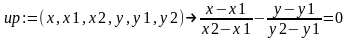
Введём координаты вершин треугольника:
>xa:=1;ya:=2;xb:=3;yb:=5;xc:=5;yc:=3;
xa := 1
ya := 2
xb := 3
yb := 5
xc := 5
yc := 3
Находим уравнение прямой АВ, подставляя в функцию up координаты вершин и :
>AB:=up(x,xa,xb,y,ya,yb);
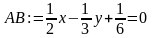
Аналогично находим уравнения прямых AC и ВС:
>AC:=up(x,xa,xc,y,ya,yc);
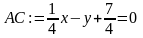
> BC:=up(x,xb,xc,y,yb,yc);
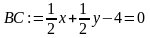
b) Введём формулу для нахождения канонического уравнения прямой, задав пользовательскую функцию upk:
>upk:=(x,x0,n1,y,y0,n2)->(x-x0)/n1-(y-y0)/n2=0;
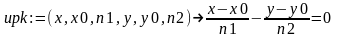
Составим
уравнение высоты CH,
выбрав в качестве
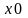 и
и
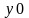 координаты точки
,
а
в качестве координат
координаты точки
,
а
в качестве координат
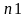 и
и
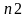 направляющего вектора координаты
вектора нормали
направляющего вектора координаты
вектора нормали
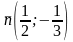 к
прямой АВ:
к
прямой АВ:
>n1:=1/2;n2:=-1/3;
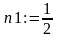
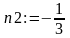
>CH:=upk(x,xc,n1,y,yc,n2);

Найдем длину высоты СН, как расстояние от точки С до прямой АВ. Для этого подключим пакет linalg и зададим вектор нормали к прямой АВ:
> with(linalg):
> n:=vector([n1,n2]);
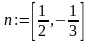
Преобразуем уравнение прямой АВ в пользовательскую функцию:
>uAB:=(x,y)->n1*x+n2*y+1/6;
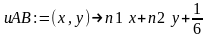
Вычислим расстояние от точки С до прямой АВ по формуле:
>dCH:=abs(uAB(xc,yc))/norm(n,2);
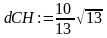
c) Найдём координаты середины отрезка ВС:
>xm:=(xb+xc)/2;ym:=(yb+yc)/2;
xm := 4
ym := 4
Найдём
уравнение медианы АМ, как уравнение
прямой проходящей через две точки
и
 :
:
>AM:=up(x,xa,xm,y,ya,ym);
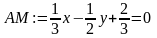
d) Найдем точку пересечения высоты CH и медианы АМ, как решение системы уравнений прямых CH и АМ:
>solve({CH,AM},{x,y});
{x = 15/4, y = 23/6}
e) Для построения треугольника подключим пакет графических функций plots:
>with(plots):
Сформируем
массивы данных для построения графиков
прямых АВ, АС, ВС, используя оператор
implicitplot(f(x,y),
x=a..b,y=c..d).
Здесь
f(x,y)-уравнение
прямой, а
интервалы
изменения x=a..b,y=c..d
выбираются так, чтобы все точки
,
,
отображались
на общем графике. Очевидно, что для этого
достаточно взять параметр a
меньше,
чем наименьшая из абсцисс
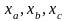 ,
а параметр b
больше,
чем наибольшая из абсцисс
,
параметр с
меньше,
чем наименьшая из ординат
,
а параметр b
больше,
чем наибольшая из абсцисс
,
параметр с
меньше,
чем наименьшая из ординат
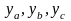 ,
а параметр d
больше,
чем наибольшая из ординат
.
,
а параметр d
больше,
чем наибольшая из ординат
.
>ab:=implicitplot(AB,x=0..6,y=0..6,color=green):
> ac:=implicitplot(AC,x=0..6,y=0..6,color=red):
> bc:=implicitplot(BC,x=0..6,y=0..6,color=black):
Выводим графики на экран:
>display([ab,ac,bc]);

2)Найти
расстояние от точки
до плоскости, проходящей через три точки
:
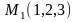 ,
,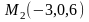 ,
,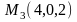 ,
,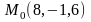 .
.
Составим сначала пользовательскую функцию для нахождения уравнения плоскости, проходящей через три точки:
> restart: with(linalg):
>pl:=matrix([[x-x1,y-y1,z-z1],[x2-x1,y2-y1,z2-z1],[x3-x1,y3-y1,z3-z1]]);
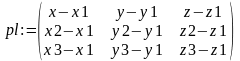
>upl:=(x,x1,x2,x3,y,y1,y2,y3)->det(pl)=0;
upl
:= (x, x1, x2, x3, y, y1, y2, y3)
 det(pl)
=
0
det(pl)
=
0
Введём координаты точек :
> x1:=1;y1:=2;z1:=3;x2:=-3;y2:=0;z2:=6;x3:=4;y3:=0;z3:=2;
x1 := 1
y1 := 2
z1 := 3
x2 := -3
y2 := 0
z2 := 6
x3 := 4
y3 := 0
z3 := 2
Найдем уравнение плоскости, проходящей через точки :
> upl(x,x1,x2,x3,y,y1,y2,y3);
8 x + 5 y + 14 z- 60=0
Вычислим теперь расстояние от точки до плоскости . Для этого сначала зададим вектор нормали к плоскости :
> n:=vector([8,5,14]);
n := [8, 5, 14]
Преобразуем уравнение плоскости в пользовательскую функцию:
>uM1M2M3:=(x,y,z)->8*x+5*y+14*z-60;
uM1M2M3 := (x, y, z) 8*x+5*y+14*z-60
Теперь вводим координаты точки :
> x0:=8;y0:=-1;z0:=6;
x0 := 8
y0 := -1
z0 := 6
Вычисляем расстояние от точки до построенной плоскости по формуле:
>rho:=abs(uM1M2M3(x0,y0,z0))/norm(n,2);