
- •Режим доступа к электронному аналогу печатного издания: http://www.Libdb.Sssu.Ru
- •Содержание
- •Предисловие
- •1 Линейная алгебра Краткий теоретический материал
- •1.1 Матрицы
- •1.2 Определители
- •1.3 Понятие алгебраического дополнения
- •1.4 Обратная матрица
- •1.5 Ранг матрицы
- •1.6 Системы линейных алгебраических уравнений
- •Лабораторная работа 1 действия над матрицами
- •Пример выполнения лабораторной работы
- •Лабораторная работа №2 вычисление ранга матрицы и нахождение обратной матрицы
- •Пример выполнения лабораторной работы
- •Лабораторная работа 3 решение систем линейных уравнений
- •Лабораторная работа 4 решение задач линейной алгебры
- •Задания
- •Варианты заданий
- •Пример выполнения работы № 1
- •Контрольные вопросы
- •2. Элементы векторной алгебры
- •2.1 Векторы
- •2.2 Скалярное произведение и его свойства
- •2.3 Векторное произведение векторов
- •Свойства векторного произведения
- •2.4 Смешанное произведение векторов
- •3. Элементы аналитической геометрии
- •3.1 Прямая на плоскости
- •3.2 Плоскость в пространстве
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
- •Пример выполнения лабораторной работы
- •Контрольные вопросы
МИНОБРНАУКИ РОССИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
Институт сферы обслуживания и предпринимательства (филиал)
«Донской государственный технический университет»
(ФРБОУ ВПО ИСОиП (филиал) ДГТУ)
линейная алгебра и
аналитическая геометрия
Лабораторный практикум
для самостоятельной работы студентов
очной, заочной и дистанционной форм обучения
всех направлений и специальностей
Шахты
ФРБОУ ВПО ИСОиП (филиал) ДГТУ
2013
У ДК
517(076.5)
ДК
517(076.5)
ББК 22.161.1я73
М34
Рекомендован к внутривузовскому изданию ИСОиП (филиал) ДГТУ
редакционно-издательским советом
Составители:
к.ф.-м.н., доцент кафедры «Математика»
А.Б. Михайлов
к.т.н., доцент кафедры «Математика»
И.Д. Михайлова
старший преподаватель кафедры «Математика»
Н.П. Величко
к.ф.-м.н., доцент кафедры «Математика»
К.А. Михайлов
Рецензенты:
к.э.н., доцент кафедры «Математика»
О.И. Охрименко
к.т.н., доцент кафедры «Математика»
О.А. Алейникова
М34 Линейная алгебра и аналитическая геометрия : лабораторный практикум : / А.Б. Михайлов, И.Д. Михайлова, Н.П. Величко, К.А. Михайлов. – Шахты : ФРБОУ ВПО ИСОиП (филиал) ДГТУ
2013. – 78 с
Лабораторный практикум предназначен в помощь студентам для подготовки и выполнения лабораторных работ по курсу линейной алгебры и аналитической геометрии.
Лабораторный практикум содержит краткий теоретический материал по изучаемым темам, варианты заданий по лабораторным работам и примеры их выполнения, а также контрольные вопросы для защиты лабораторных работ. Рекомендован для студентов очной, заочной и дистанционной форм обучения всех направлений и специальностей ИСОиП.
УДК 517(076.5)
ББК 22.161.1я73
Режим доступа к электронному аналогу печатного издания: http://www.Libdb.Sssu.Ru
© ФРБОУ ВПО ИСОиП (филиал) ДГТУ , 2013
Содержание
Предисловие…………………………………………………………………
1 Линейная алгебра. Краткий теоретический материал…………………..
1.1 Матрицы………………………………………………………………….
1.2 Определители…………………………………………………………….
1.3 Понятие алгебраического дополнения…………………………………
1.4 Обратная матрица………………………………………………………
1.5 Ранг матрицы……………………………………………………………
1.6 Системы линейных алгебраических уравнений……………………
Лабораторная работа 1. Действия над матрицами………………………
Лабораторная работа 2. Вычисление ранга матрицы и нахождение обратной матрицы…………………………………………………………………………….
Лабораторная работа 3. Решение систем линейных уравнений……………….
Лабораторная работа 4. Решение задач линейной алгебры с использованием пакета прикладных программ Maple…………………………………………..
2 Элементы векторной алгебры. Краткий теоретический материал…………..
2.1 Векторы…………………………………………………………………………
2.2 Скалярное произведение векторов и его свойства…………………………..
2.3 Векторное произведение векторов и его свойства…………………………..
2.4 Смешанное произведение векторов и его свойства…………………………
3 Элементы аналитической геометрии. Краткий теоретический материал
3.1 Прямая на плоскости…………………………………………………………..
3.2 Плоскость в пространстве…………………………………………………….
Лабораторная работа 5. Элементы векторной алгебры…………………………
Лабораторная работа 6. Прямая и плоскость……………………………………
Предисловие
Последние десятилетия отмечены бурным вторжением математики во все сферы человеческой деятельности. Возросла роль курса вычислительной математики в процессе вузовской подготовки. Современный специалист обязан владеть методами вычислительной математики и уметь выбирать среди них наиболее подходящий для решения конкретной задачи.
Целью практикума является формирование навыков решения основных задач линейной алгебры и аналитической геометрии. Лабораторные работы выполняются с использованием таблиц EXCEL и с привлечением математического пакета MAPLE. Предложен теоретический материал по разделам «Линейная алгебра» и «Аналитическая геометрия».
Практикум имеет следующую структуру:
• краткий теоретический материал по линейной алгебре и аналитической геометрии;
• лабораторные работы по разделам дисциплины, включающие последовательное описание их выполнения;
• варианты, предлагаемые студентам для самостоятельного выполнения;
• контрольные вопросы для защиты лабораторных работ.
Студент должен выполнить свой вариант лабораторной работы и оформить отчёт по работе, который должен содержать:
• название лабораторной работы;
• цель работы;
• задание своего варианта;
• результаты решения на ЭВМ;
• анализ полученного решения, интерпретация результатов;
• выводы.
Настоящее пособие позволит студентам понять, как применять математическую теорию на практике.
1 Линейная алгебра Краткий теоретический материал
1.1 Матрицы
Прямоугольная таблица чисел
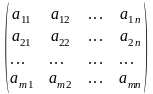 ,
,
содержащая
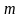 строк и
строк и
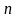 столбцов, называется матрицей
размеров
столбцов, называется матрицей
размеров
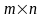 .
Числа
.
Числа
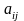 называются элементами
матрицы.
Каждый элемент матрицы снабжен двумя
индексами: первый индекс указывает
номер строки, второй – номер столбца,
в которых расположен этот элемент. Часто
вместо подробной записи употребляют
сокращенную:
называются элементами
матрицы.
Каждый элемент матрицы снабжен двумя
индексами: первый индекс указывает
номер строки, второй – номер столбца,
в которых расположен этот элемент. Часто
вместо подробной записи употребляют
сокращенную:
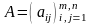 или даже
или даже
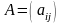 .
Если число строк матрицы равно числу
ее столбцов, то матрица называется
квадратной
порядка
.
Диагональ
.
Если число строк матрицы равно числу
ее столбцов, то матрица называется
квадратной
порядка
.
Диагональ
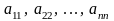 квадратной матрицы называется главной
диагональю,
а диагональ
квадратной матрицы называется главной
диагональю,
а диагональ
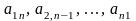 – побочной
диагональю.
– побочной
диагональю.
Среди
квадратных матриц одного и того же
порядка (например, порядка
,
т.е. размеров
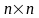 )
важную роль играет матрица вида
)
важную роль играет матрица вида
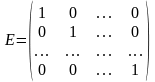 ,
,
которую называют единичной матрицей.
Умножение
матрицы на число.
Для того чтобы умножить матрицу
на число
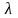 ,
нужно каждый элемент матрицы
,
нужно каждый элемент матрицы
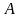 умножить на это число:
умножить на это число:
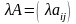 .
.
Сложение
матриц.
Складывать можно только матрицы с
одинаковым числом строк и столбцов,
т.е. матрицы одинаковых размеров. Суммой
матриц
и
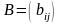 называется матрица
называется матрица
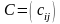 ,
элементы которой равны суммам
соответствующих элементов матриц
и
,
элементы которой равны суммам
соответствующих элементов матриц
и
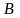 ,
т.е.
,
т.е.
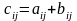 для любых индексов
для любых индексов
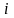 ,
,
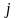 .
.
Умножение
матриц.
Произведение матрицы
на матрицу
(обозначается
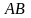 )
определено только в том случае, когда
число столбцов матрицы
равно числу строк матрицы
.
В результате умножения получим матрицу
)
определено только в том случае, когда
число столбцов матрицы
равно числу строк матрицы
.
В результате умножения получим матрицу
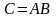 ,
у которой столько же строк, сколько их
в матрице
,
и столько же столбцов, сколько их в
матрице
.
Для удобства запоминания запишем это
кратко:
,
у которой столько же строк, сколько их
в матрице
,
и столько же столбцов, сколько их в
матрице
.
Для удобства запоминания запишем это
кратко:
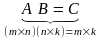
Если
,
и
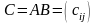 ,
то элементы
,
то элементы
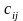 определяются следующим образом:
определяются следующим образом:
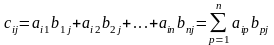 ,
,
где
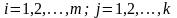 .
.
Это правило можно сформулировать и словесно: элемент , стоящий на пересечении -й строки и -го столбца матрицы , равен сумме попарных произведений соответствующих элементов -й строки матрицы и -го столбца матрицы . Другими словами, элемент является результатом скалярного произведения -й вектор-строки и -го вектор-столбца.
