3.3.1. Механізми змішаного фінансування проектів

Підготовка і реалізація будь-яких проектів, спрямованих на забезпечення функціонування або розвитку організаційної системи (виробничої системи, фірми, галузі, регіону, економіки загалом тощо), об’єктивно відбувається в умовах обмеженості фінансових ресурсів. Тому постає задача організації оптимального використання їх або такого розподілу ресурсів між виконавцями, який задовольняє їхні інтереси та забезпечує досягнення максимального загального економічного ефекту від реалізації проекту. Задача фінансування проекту в цьому разі належить до класу задач розподілу наявного ресурсу ОС способом організації взаємодії між її учасниками.

Обмеженість бюджету ОС часто не дає змоги реалізувати необхідну кількість проектів, а тому виникає необхідність залучення фінансових ресурсів

фірм (виконавців), які пропонують ці проекти. У зв’язку з цим потрібна організація механізму змішаного фінансування проекту, сутність якого полягає у використанні як бюджетних коштів ОС на реалізацію проекту, так і фінансових ресурсів, що зобов'язуються виділити виконавці.

Для формалізації механізму організації змішаного фінансового забезпечення проекту вводяться такі позначення:

і — індекс виконавця, ;

— сумарна вартість проекту і-того виконавця (заявка виконавця);

— обсяг фінансування проекту і-того виконавця керівним органом;

— загальний дохід від реалізації проекту і-того виконавця;

— дохід і-того виконавця від реалізації проекту у разі його повного фінансування GB;

R — обсяг бюджетних коштів;

— механізм змішаного фінансування проектів.

Очевидно, означає обсяг фінансових ресурсів, що виконавець зобов’язується забезпечити за свій рахунок. Тоді дохід виконавця становитиме

. (1)

Без втрати спільності можна вважати, що R = 1. У цьому разі має місце нерівність , тобто GB виділяє виконавцю коштів більше від заявленої суми, а різниця залишається у виконавця.

Задача керівництва організаційної системи (GB) полягає в розробленні такого механізму фінансування проектів, який забезпечував би максимальний дохід від реалізації їх:

,

де — рівноважні стратегії виконавців, або точка Неша відповідної гри.

Цілком зрозуміло, що механізми фінансування проектів різняться між собою залежно від функцій доходу.

Розглянемо випадок лінійного виду функцій доходу, тобто коли

, , , , ,

де — величини питомих доходів.

Раніше ми розглядали механізм прямих пріоритетів у вигляді

, , (2)

де — пріоритет і-того виконавця.

Для визначення ситуації рівноваги Неша здійснюють перетворення (1) з урахуванням (2) та припущення, що R = 1:

.

З умови максимуму цієї функції по при , отримують

, .

З урахуванням умов та або визначають

, .

Якщо не виконуються умови , пропозиції відповідних виконавців відхиляють і розрахунки повторюють з урахуванням нових значень i n. Цю процедуру продовжують в ітераційному режимі до отримання ситуації рівноваги, тобто виконання цієї умови.

При кількість виконавців, залучених до здійснення проектів, визначають як максимальне k, що задовольняє умову:

, .

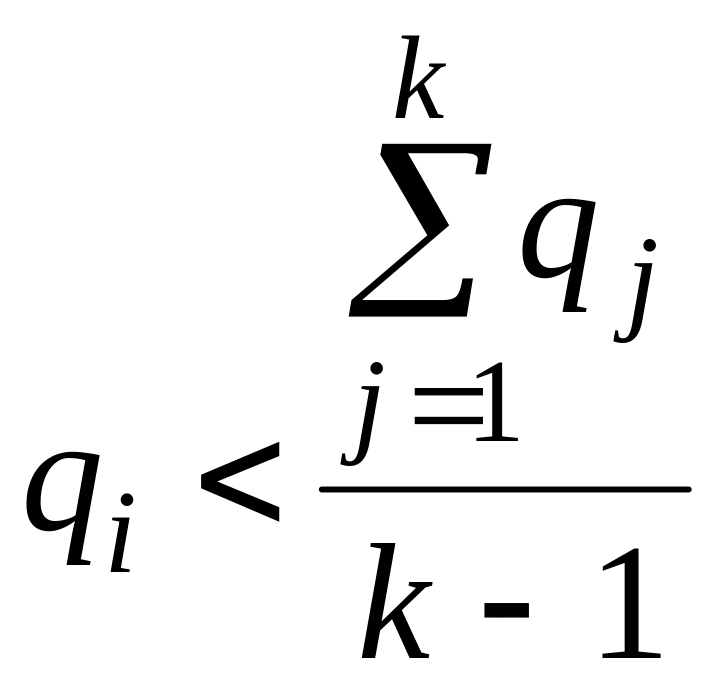Задача визначення механізму прямих пріоритетів, що забезпечують максимум загального доходу, полягає в оптимізації множини змінних , за яких досягає максимуму функціонал

. (3)

Ввівши заміну , , , , , (3) перетворюють до вигляду

, (4)

де .

Задача полягає у визначенні , за яких досягає максимуму функціонал (4). ЇЇ рішення, отримане за допомогою методу множників Лагранжа, має вигляд

, ,

звідки з точністю до постійного множника оптимальні пріоритети визначають за формулою

, .

Розглянемо тепер випадок нелінійного виду функцій доходу, який отримує і-тий виконавець. Для визначеності використовуватимемо показовий вид функції, тобто

, .

Як і раніше, розглядають механізм прямих пріоритетів і використовують гіпотезу слабкого впливу, тобто виконавці не враховують впливу своїх заявок на 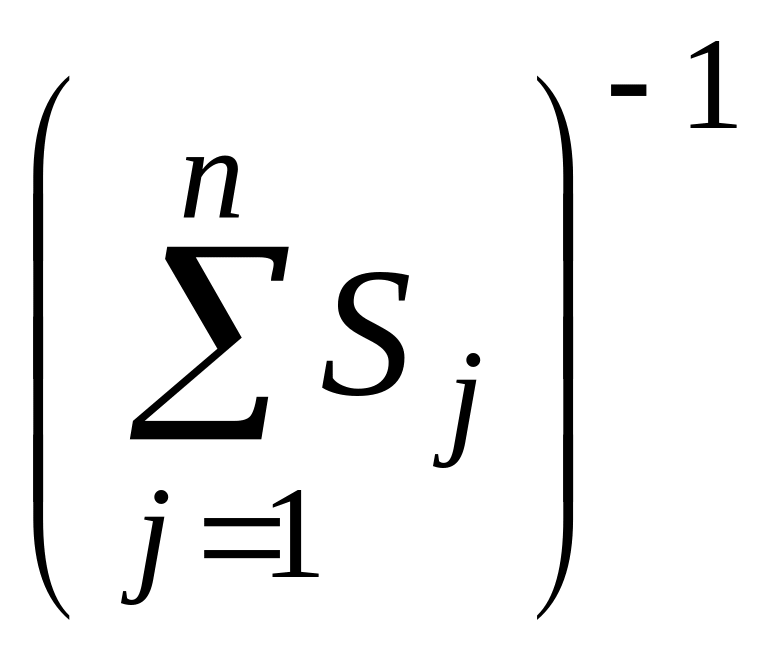. Тому рівноважну заявку і-того виконавця визначають за формулою , де S визначають із рівняння:

, . (5)

З очевидної нерівності при H > 1 випливає, що рішення рівняння (5) задовольняє нерівності .

Отже, у разі нелінійного виду функцій доходу механізм змішаного фінансування забезпечує обсяг залучення коштів виконавців більший, ніж у разі безпосереднього фінансування виконавцями проектів. Дійсно, за безпосереднього фінансування i-тий виконавець матиме максимум прибутку за обсягу фінансування , а тому обсяг сумарного залучення коштів виконавців у разі прямого фінансування становитиме H.

Після заміни рівняння (5) набуває вигляду

,

звідки видно, що зі зростанням зростає u. Таким чином, дохід від механізму змішаного фінансування тим більший, чим більший параметр у функціях доходу виконавців.