Объем выборки и надежность

Под объемом выборки понимается число наблюдений за поведением одного варианта системы (если проводится факторный эксперимент, то каждый набор значений факторов определяет один вариант системы).

Под надежностью понимается статистическая точность выборочной оценки. Она выражается, например, длиной доверительного интервала и доверительной вероятностью (1-).

При проведении имитированных экспериментов нам приходится решать две задачи:

1. Для заранее установленного объема выборки (числа повторения опытов) найти надежность оценки.

2. При фиксированной желаемой надежности определить требуемый объем выборки.

При определении надежности первой задачей является оценивание дисперсий. На основе этого вычисляется доверительный интервал.

Стандартные методы построения доверительного интервала основаны на предположении независимости и нормальности наблюдений. В имитационной модели предположение о нормальности можно удовлетворить, если откликом одного опыта сделать среднее значение интересующей нас величины в течение одного опыта.

Соответствующая предельная теорема показывает, что среднее даже зависимых наблюдений распределено примерно нормально. Более существенным является предположение о независимости результатов различных имитационных опытов. Проще всего независимые опыты могут быть получены повторениями с помощью различных последовательностей случайных чисел. Но при этом возможно получение смещенных результатов из-за наличия неустановившихся режимов работы модели.

Другой подход - это деление удлиненного опыта на подопыты. Средние значения откликов в каждом подопыте дают нам требуемые данные. В любом случае доверительный интервал для интересующей нас величины строится с помощью распределения Стьюдента со степенями свободы (n -1), где n число наблюдений, или объем выборки:

– квантиль распределения Стьюдента

Кроме оценки среднего (*) можно применять для проверки гипотез о среднем. Если мы хотим проверить гипотезу о том, что Е(х) = _о, то мы смотрим, содержится ли _o в найденном доверительном интервале. Если нет, то гипотезу отвергаем.

При проверке различных средних значений двух моделей мы имеем две нормально распределенные совокупности:

.

Мы имеем независимые наблюдения за моделями:

Существует несколько способов сравнить среднее:

Первый способ

Наблюдения х₁ и х₂ можно спарить, применяя общие случайные числа, тогда х_1i и х_2i будут зависимыми, а сами пары (х_1i,х_2i) останутся независимыми. Тогда мы можем рассматривать величины

.

В этом случае мы возвращаемся к задаче проверки гипотезы о равенстве математического ожидания Е(d)= 0. Эта задача решается с помощью критерия Стьюдента.

Второй способ

Если обе совокупности имеют одинаковую дисперсию:

,

то можно воспользоваться стандартным критерием Стьюдента. Доверительный интервал здесь будет:

где -оценка.

Третий способ

.

В этом случае можно воспользоваться следующим подходом.

Пусть .

В этом случае доверительный интервал:

,

Причем, здесь при вычислении х₂ использованы все n₂ значений опытов со второй моделью, а при определении U_i только n₁ первых значений опытов со второй моделью.

Определение необходимого количества имитационных опытов при заданной надежности происходит следующим образом.

Пусть известно, что закон распределения переменной отклика нормальный с дисперсией ². Если мы хотим, чтобы с вероятностью (1-) оценка среднего отличалась от истинного значения не более чем на С единиц, мы используем уравнение:

, - истинное ср. значение

Поскольку x - среднее n независимых нормально распределенных случайных величин, то можем записать:

,

²(x) – значение дисперсии отклика x при одном имитационном опыте.

Z^/2 – квантиль нормального распределения.

Т.о., можно записать, что:

Это есть искомое число опытов, которые надо провести, чтобы получить оценку с требуемой надежностью. Однако в имитационном моделировании величина ²(x) неизвестна, поэтому вместо нее мы поставим ее оценку S²(x) и используем критерий Стьюдента с (n -1) степенями свободы. Т.е. получим:

Как видно из этого выражения значение n зависит от результатов экспериментов S² (x) и от самого себя .

Лекция 13

Поэтому более подходящей является итеративная процедура определения числа имитационных опытов n по следующей совокупности неравенств:

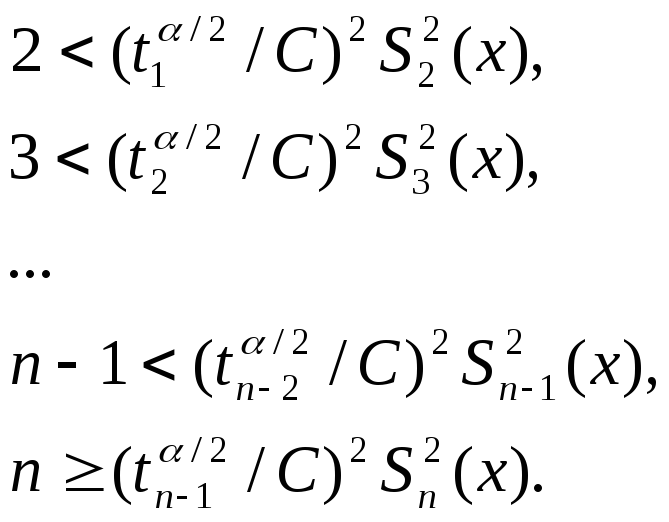
здесь S_i² (x), i=2,3,..., n - последовательная оценка дисперсии ²(x) по результатам i наблюдений.

Эти оценки не являются независимыми и, следовательно, вероятность интересующего события подсчитать трудно. Она необязательно окажется равной (1-).

Подобная процедура определения количества опытов называется процедурой автоматического останова.

Другой способ – это схема двойной выборки. Первоначально проводится n₀ имитационных опытов, по которым оцениваются ² с (n_o-1) степенями свободы. Полученная оценка S²_no дает количество требуемых опытов:

.

После этого проводятся n-n_o опытов.

Проблемой при таком подходе является выбор значения n_o. Большое значение n_o дает уменьшение квантиля , но может привести к лишним опытам, когда n_o > n. Т.к. в имитационном моделировании опыты обычно дороги, то чаще применяют более эффективную последовательную процедуру.

Рассмотрим теперь ситуацию в сравнении двух моделей. Для известных дисперсий ₁² и ₂² , исследуемых значений первой и второй модели мы имеем, что

.

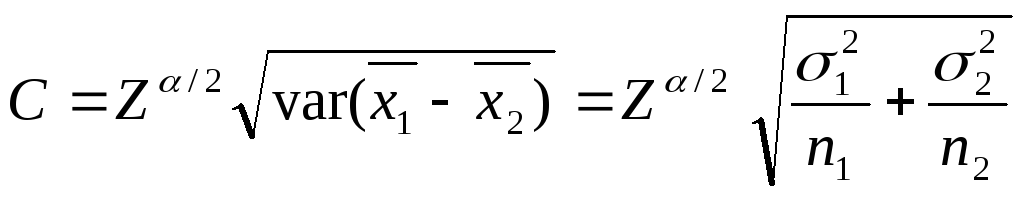Дисперсия () минимальна для фиксированного общего объема выборки n = n₁+n₂ при выполнении соотношения:

,

Поэтому

.

Следовательно,

.

Отсюда

А общее число опытов:

что позволяет получить доверительный интервал с размахом С и вероятностью (1-).

Для неизвестных дисперсий предлагается следующий последовательный подход:

а). Пусть на очередном шаге произведено n₁ и n₂ опытов над соответствующими моделями. Вычисляются оценки для дисперсий и :

Если , то следующий опыт будет проводиться над первой моделью, в противном случае - над второй.

б). Для n = n₁+ n₂ вычисляется величина

.

Дальнейшее проведение опытов прекращается, как только осуществляется одно из следующих условий:

1..

2..

3. или .

Организационные аспекты имитационного моделирования

Согласно исследованиям, построение модели объекта в среднем занимает 10.1 месяца. Средняя группа работающих над моделью - 2.5 человека. Для разработки одной машинной модели-имитатора сложной системы требуются специалисты различных профилей:

• в области исследования операций;

• статистики;

• программирования;

• системного анализа;

Также требуются специалисты конкретной предметной области. Но не все специалисты нужны одновременно.

На ранних стадиях разработки необходимы лишь специалисты по исследованию операций и специалисты-отраслевики. Экспертные оценки могут потребоваться на различных стадиях выполнения проекта.

Программисты и аналитики включаются в число разработчиков лишь после завершения создания программного обеспечения для первых грубых моделей системы.

Главная цель создаваемой модели - помочь руководителю повысить качество управления. Поэтому перед созданием модели необходимо вникнуть как в сам процесс принятия решения, так и в функции лица, принимающего решения (ЛПР).

Необходимые и достаточные условия существования ситуации принятия решения предполагают наличие:

• цели, которую хочет достичь ЛПР;

• по крайней мере, двух альтернативных вариантов решения;

• сомнения ЛПР о том, какую из альтернатив предпочесть.

Необходимо обратить внимание на следующий аспект принятия решения: каждое решение содержит элементы двух типов - фактографические, ценностные.

Фактографические элементы представляют собой данные о наблюдении мира и его закономерностей; их можно и нужно проверять на истинность и ложность.

Ценностные элементы содержат этические и моральные характеристики принимаемого решения. Правомерность их проверить невозможно.

Такое же разделение характерно и для целей, стоящих перед руководителем при принятии решения. Поэтому большинство проблем, связанных с принятием решения, содержат как объективные, так и субъективные элементы. Поэтому весьма полезным оказывается тесное сотрудничество с ЛПР при разработке модели. В результате этого ценностные элементы могут найти свое отражение в моделях.

В других случаях необходимо, чтобы модель как можно точнее воспроизводила реальный объект по всем его фактическим или объективным характеристикам. ЛПР, используя результаты моделирования, накладывает на них свои ценностные предпочтения для вынесения окончательного решения.

Модели используются в двух различных целях:

1. В научном плане - это один из этапов в цепи формирования гипотез, построения моделей, предсказания будущего поведения системы и оценки результатов. Здесь обычно судят о модели по ее качеству. Хорошей моделью считается нетривиальная, мощная и изящная модель. Нетривиальная модель вскрывает детали, невидимые при непосредственном наблюдении. Мощная модель позволяет получить много таких нетривиальных деталей. Изящная модель имеет простую структуру и легко рассчитывается на компьютере.

2. Руководители используют модель для выявления ценностных альтернатив решения проблемы. С их точки зрения хорошая модель - это релевантная, точная, результативная и экономичная. Модель считается релевантной, если она предназначена для решения важных для руководителя проблем. Модель точная, если результаты обладают высокой степенью достоверности. Результативная модель, если получаемые результаты могут найти успешное применение. Модель экономичная, если эффект от внедрения превышает расходы на ее создание и использование.

При создании групп по разработке модели желательно вводить в группу следующих специалистов:

• одного или нескольких специалистов по системному анализу; они должны иметь опыт по применению используемых методов к решению конкретных задач по принятию управленческих решений;

• одного или нескольких специалистов по вычислительной технике; такой специалист должен быть не просто программистом, но и аналитиком, он должен сам уметь строить модель, но его основные усилия должны быть направлены на использование компьютера для обработки данных и получения результатов на основе применения математических методов;

• одного или нескольких эрудированных лиц, хорошо знающих организацию, ее людей и особенно ее проблемы;

• одного или нескольких сотрудников организаций, представляющих отдел, который заинтересован в решении проблемы.

Важным фактором в разработке, программировании и применении модели является способ построения машинной программы.

Наиболее применимым способом здесь является модульное программирование. Его можно определить, как систему построения программы из набора отдельных взаимосвязанных блоков (модулей), с помощью различных сочетаний которых можно получить отдельную программу.

При противоположном подходе (построение монолитных программ) возникают следующие проблемы:

1. Практически невозможна полная проверка программы; это объясняется большим числом общих логических построений, сложными взаимосвязями и невозможностью выделить ключевые участки программы для испытаний;

2. В алгоритм невозможно внести изменения без серьезной переделки программы;

3. Работа всей группы зависит от постоянного участия в ней программиста - разработчика такой программы.

При модульном программировании каждым модулем реализуется определенная логическая функция (или несколько логических функций). Для того, чтобы определить какие подсистемы и логические функции понадобятся в программе, проводится предварительный анализ проблем. После того, как они выявлены, каждый модуль кодируется и отлаживается отдельно. Руководителю разработки желательно придерживаться следующих правил при программировании:

• модульный подход;

• использование коротких (до 50 строк) основных программ и подпрограмм;

• начинать каждую основную программу и подпрограмму комментарием;

• составление полной документации программы.

Полное документирование предполагает наличие блок-схемы, алгоритмов каждого модуля и всей программы, описание входных данных, необходимых для работы программы, т.е. место расположения входных данных и требуемое поле записи, описание переменных программы, не используемых в качестве входных, словесное описание задач и функций всех модулей, пусковые характеристики, необходимые для выполнения программы на требуемом компьютере, тестовые примеры.

Так как имитационная модель создается для пользователя, то и информация, полученная с ее помощью, должна быть приемлема для него же. Критерии приемлемости включают надежность и полезность информации.

Выходные данные модели должны быть разумными, т.е. модель не должна давать абсурдных ответов, даже если на вход подаются абсурдные данные.

Второй аспект применимости состоит в том, что заказчик-пользователь должен понимать, как можно использовать результаты моделирования.

С достижением конечной цели тесно связано требование реалистичности данных, необходимых для использования модели. Реалистичные данные должны быть достаточно надежными, доступными и получаемыми за разумную плату.

Кроме того, ИМ должна позволять администратору оценивать и те решения, которые удовлетворяют его собственным понятиям рациональности, а также возможные результаты применения сформулированных им стратегий.

Подготавливая результаты исследования для предоставления их заказчику, рекомендуется придерживаться следующих правил:

1. Письменным отчетам следует предпочесть устные сообщения с одновременным использованием хорошо продуманных демонстрационных средств;

2. Одному большому формальному изложению результатов следует предпочесть серию небольших неформальных обсуждений;

3. Необходимо делать упор на логику вашего подхода к решению задач;

4. В первом докладе необходимо четко описать принятые допущения и ограничения;

5. Необходимо тщательно описать целевую функцию и выходные переменные модели;

6. Тщательно описать концептуальный подход, основные взаимосвязи, переменные и обоснования выбранного способа интерпретации результатов;

7. Дать общую оценку, а также перечислить все достоинства и недостатки рассмотренных альтернатив и результатов, полученных с помощью модели.