Основные параметры переходной функции:
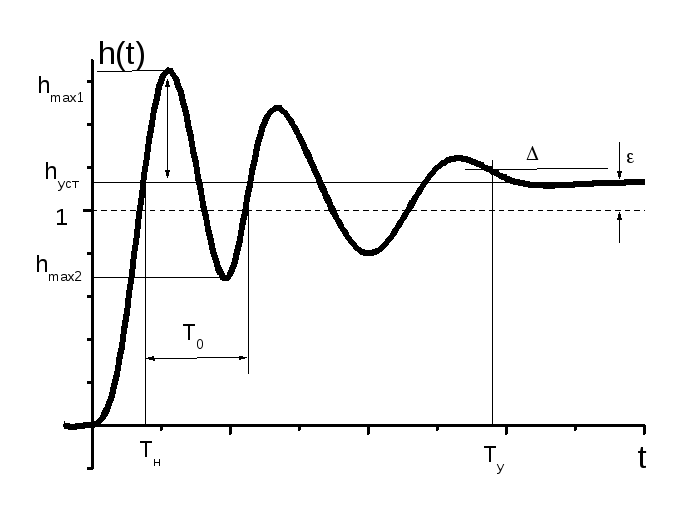
Рис. 2.8. Переходная характеристика САУ.
-
статическое
отклонение
(статическая ошибка) ε = 1(t)
– hуст.
Она характеризует разность между
входным и выходным сигналами в
установившемся режиме. Системы, у
которых статическое отклонение не
равно нулю (ε <> 0) называются
статическими.
Системы, у которых ε = 0, называются
астатическими.
-
Динамическое
отклонение,
т.е. разность между максимальным
отклонением и установившемся значением
hmax
– hуст.
-
Время
регулирования
(управления) Tу
– это время переходного процесса. Это
время, после которого разность между
текущим значение выходного сигнала и
установившимся значением будет иметь
малую величину Δ. Как правило, Δ принимают
равным 5% от hуст.
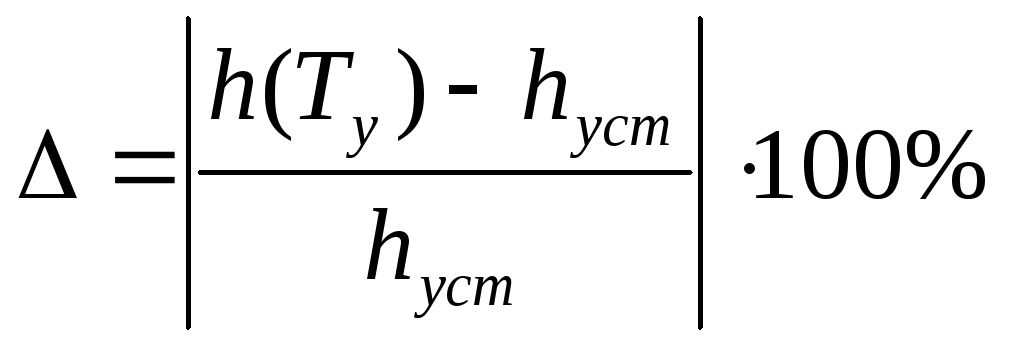
Время регулирования
характеризует быстродействие системы
автоматического управления. Чем меньше
Tу,
тем выше быстродействие.
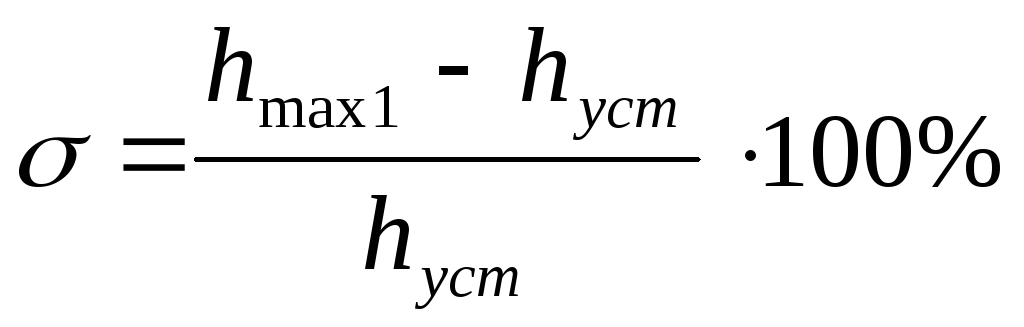
(В реальных системах
перерегулирование обычно составляет
10 – 30%).
-
Частота
колебаний процесса
ω = 2π/T0,
где T0
– период колебаний.
-
Время нарастания
(установления) Tн
– время, за которое система достигает
установившегося значения.
-
Логарифмический
декремент затухания,
определяется по формуле:
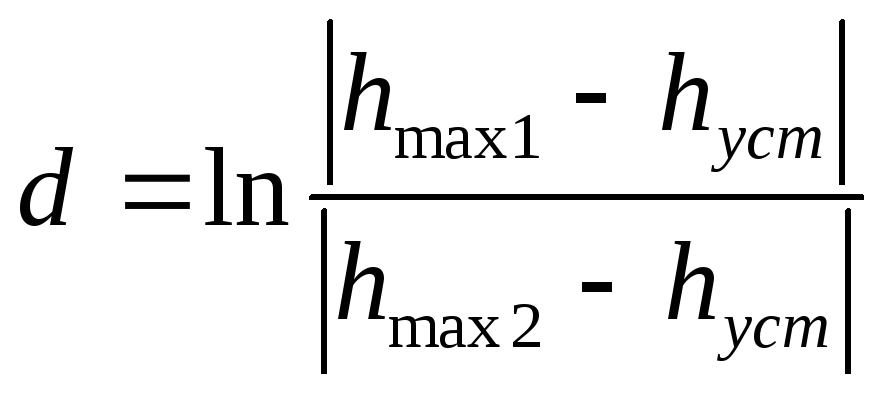
Функции 1(t)
и δ(t)
можно использовать для экспериментального
определения передаточной функции
элемента системы управления:

Первый подход:
подадим на вход *(t).
Пусть *(t)
≈
(t)
(т.к. (t)
физически не реализуема), измерим w*(t)
≈
w(t).
Теперь можно вычислить L[w*(t)]
= W*(s)
≈ W(s).

Второй подход:
На вход подаем 1(t). Измеряем h(t)
и вычисляем передаточную функцию. W(s)
= L[d/dt(h(t)].




