
Лекции по Теории автоматического управления (ТАУ) / ТАУ ЛЕКЦИЯ 6
.doc
ЛЕКЦИЯ 6.
Структурные схемы систем автоматического управления
Систему автоматического управления можно рассматривать как комбинацию динамических звеньев (типовых и нетиповых). Каждое звено имеет определенное математическое описание, выраженное чаще всего в виде передаточной функции W(s). Зная математическое описание звеньев и связи между ними, всегда можно получить математическое описание всей системы в целом. Для представления системы управления с помощью динамических звеньев используют структурные схемы.
Дадим определение структурной схемы. Структурной схемой называется изображение системы управления в виде совокупности типовых и нетиповых динамических звеньев с указанием связей между ними.
Основными элементами структурных схем являются следующие.
1. Динамическое звено. Звено в структурной схеме выступает как элементарная структурная единица, преобразователь информации (сигнала). В поле звена указывается его математическое описание (передаточная функция W(s)).

Как правило, звено имеет один вход и один выход, однако допускается также использование в структурных схемах звеньев с несколькими входами и одним выходом. Тогда возле каждого входа указывается своя передаточная функция. Выходной сигнал в этом случае будет определяться выражением:
Y(s) = W1(s)X1(s) + W2(s)X2(s) + …

2. Линия передачи сигнала (линия связи). Устанавливает связь между звеньями. Стрелка указывает направление передачи сигнала.

3. Разветвление (узел). Используется, когда один и тот же сигнал поступает на разные звенья системы управления.

4. Сумматор. Используется, когда сигналы преобразуются в новый сигнал, равный сумме исходных. Поскольку сигналы в одной системе управления могут иметь разную физическую природу, то следует особо отметить, что суммируемые сигналы должны иметь одинаковую размерность (нельзя, например, складывать электрическое напряжение с током).


5. Элемент сравнения. Формирует сигнал, равный разности входных сигналов. Элемент сравнения можно рассматривать как сумматор с инвертированным входом. Встречается два варианта обозначения вычитаемого сигнала, поступающего на вход элемента сравнения: 1) сектор, соответствующий входу вычитаемого сигнала, выделяется цветом; 2) вход вычитаемого сигнала указывается знаком минус.


Преобразование структурных схем
При расчетах систем автоматического управления может возникнуть необходимость в преобразовании структурной схемы для приведения ее к более простому виду или к виду, более удобному для решения некоторой конкретной задачи. Исходная и преобразованная структурные схемы должны быть эквивалентными, т.е. одинаковым образом отражать динамические свойства системы управления.
Любая структурная схема включает в себя последовательно и параллельно соединенные звенья, а также элементы соединенные обратной связью. Звенья соединенные подобным образом можно заменить на одно звено, имеющее эквивалентную передаточную функцию.
Последовательное соединение звеньев
Последовательным называется такое соединение звеньев, при котором выходная величина одного звена подается на вход последующего звена.

Для этого соединения справедливы следующие соотношения:
Y1(s) = W1(s)·X(s) Y(s) = W2(s)·Y1(s) = W1(s)·W2(s)·X(s) = Wэ(s)·X(s)
Wэ(s) = W1(s)·W2(s)
Для случая последовательного соединения n звеньев имеем:
Wэ(s) = W1(s)·W2(s)·…·Wn(s)
Другими словами, эквивалентная передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев. Таким образом цепочку параллельных звеньев в структурной схеме можно заменить одним звеном с передаточной функцией Wэ(s) = W1(s)·W2(s)·…·Wn(s).
Параллельное соединение звеньев
Параллельным называется такое соединение звеньев, при котором на вход всех звеньев подается один и тот же сигнал, а выходные сигналы от всех звеньев суммируются.

Для этого соединения справедливы следующие соотношения:
Y(s) = Y1(s) + Y2(s) + Y3(s) = W1(s)·X(s) + W2·X(S) + W3(s)·X(s) =
= [W1(s) + W2(s) + W3(s)]·Y(s) = Wэ(s)·X(s)
Wэ(s) = W1(s) + W2(s) + W3(s)
Для случая параллельного соединения n звеньев имеем:
Wэ(s) = W1(s) + W2(s) +…+ Wn(s)
Другими словами, эквивалентная передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев. Таким образом цепочку параллельных звеньев в структурной схеме можно заменить одним звеном с передаточной функцией Wэ(s) = W1(s) + W2(s) +…+ Wn(s).
Соединение звеньев с обратной связью
Соединение с обратной связью имеет прямую цепь передачи сигнала и цепь обратной связи. Обратная связь может быть отрицательной и положительной. При отрицательной обратной связи на вход прямой цепи подается разность межу входным сигналом х(t) и выходным сигналом линии обратной связи. При положительной обратной связи эти величины складываются.

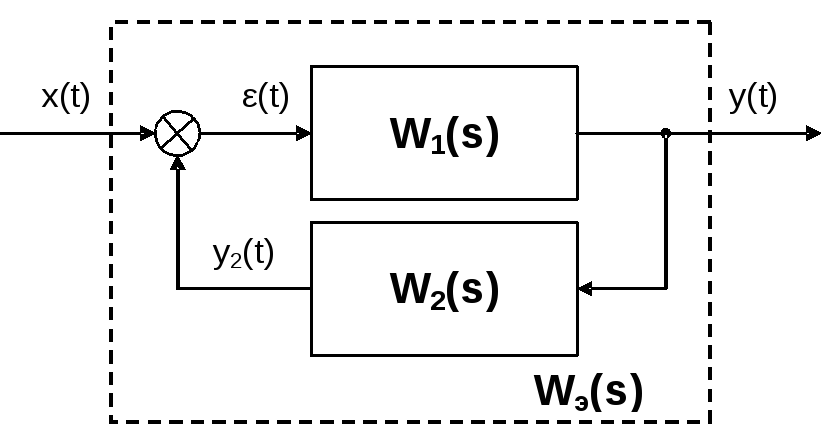
Для соединения с отрицательной обратной связью справедливы следующие соотношения:
Y(s) = W1(s)·E(s) = W1(s)·[X(s) – Y2(s)] Y2(s) = W2(s)·Y(s)
Y(s) = W1(s)·X(s) – W1(s)·Y2(s) = W1(s)·X(s) – W1(s)·W2(s)·Y(s)
Y(s) + W1(s)·W2(s)·Y(s) = Y(s)·[1 + W1(s) ·W2(s)] = W1(s)·X(s)
Y(s) = W1(s)/[1 + W1(s)·W2(s)]·X(s)
В итоге получаем следующее выражение для эквивалентной (результирующей) передаточной функции:
Wэ(s) = W1(s)/[1 + W1(s)·W2(s)]
Для случая соединения с положительной обратной связью получается аналогичное выражение для эквивалентной передаточной функции, только при этом знак плюс в знаменателе изменяется на знак минус:
Wэ(s) = W1(s)/[1 – W1(s)·W2(s)]
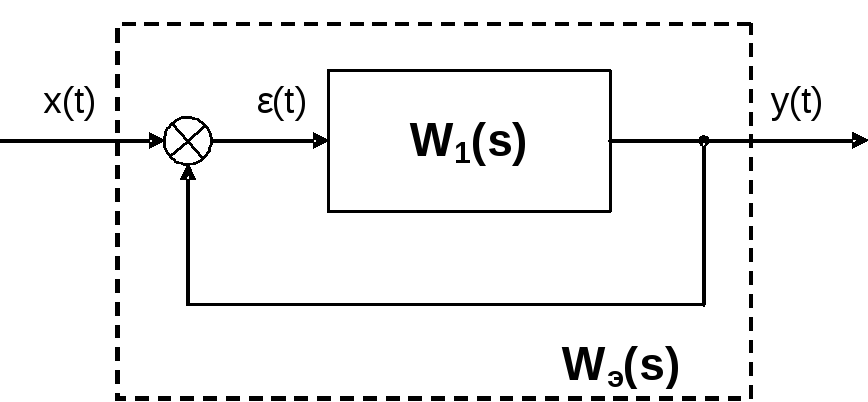
Частным случаем соединения с обратной связью является ситуация, когда выходной сигнал от прямой цепи передается без изменения на элемент сравнения или сумматор. Такие обратные связи называются единичными, т.к. у них передаточная функция в обратной цепи равна единице (W2(s) = 1). Тогда эквивалентные передаточные функции для отрицательной и положительной обратной связи упрощаются и принимают следующий вид, соответственно:
Wэ(s) = W1(s)/[1 + W1(s)]
Wэ(s) = W1(s)/[1 – W1(s)]

Правила преобразования структурных схем
В тех случаях, когда структурная схема оказывается слишком сложной, например, содержит перекрестные связи, ее упрощают пользуясь правилами преобразования структурных схем. Смысл этих правил состоит в переносе элементов структурной схемы из одного положения в другое, так чтобы при этом сохранялась эквивалентность структурных схем.
-
Перенос узла через звено.

Чтобы перенести узел через звено с передаточной функцией W(s), необходимо включить в линию, не проходящую через звено (выход 2), дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Действительно, сигнал у(t) после такого переноса не изменится, а сигнал на выходе 2 будет равен: Х(s)·W(s)·1/W(s) = Х(s), т.е. он совпадает с исходным сигналом х(s).
-
Перенос звена через узел.

Чтобы перенести звено с передаточной функцией W(s) через узел, необходимо включить в обе линии звенья с передаточной функцией W(s). Легко убедиться, что эквивалентность структурных схем при этом сохраняется.
-
Перенос сумматора через звено.

Сразу отметим, что данное правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения, т.к. элемент сравнения можно рассматривать как сумматор с инвертированным входом.
Чтобы перенести сумматор через звено с передаточной функцией W(s), необходимо к обоим входам на сумматор добавить дополнительный элемент – звено с передаточной функцией W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·[X1(s) X2(s)]; выходной сигнал на преобразованной схеме равен: Y(s) = W(s)X1(s) W(s)X2(s), т.е. выходные сигналы совпадают.
-
Перенос звена через сумматор.

Это правило преобразования структурных схем также применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести звено с передаточной функцией W(s) через сумматор, необходимо в линию без звена (вход 2) включить дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·X1(s) X2(s); выходной сигнал на преобразованной схеме равен: Y(s) = W(s)·[X1(s) 1/W(s)·X2(s)] = W(s)·X1(s) X2(s), т.е. выходные сигналы совпадают.
-
Перенос узла через сумматор.

Чтобы перенести узел через сумматор, необходимо в схему включить дополнительный элемент – элемент сравнения. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х1(t) + х2(t) и х1(t) = у(t) – х2(t) = х1(t) + х2(t) – х2(t).

При применении этого правила преобразования структурных схем для переноса узла через элемент сравнения в схему необходимо включить дополнительно не элемент сравнения, а сумматор. Эквивалентность этих схем также легко проверить: у(t) = х1(t) – х2(t) и х1(t) = у(t) + х2(t) = х1(t) – х2(t) + х2(t).
-
Перенос сумматора через узел.
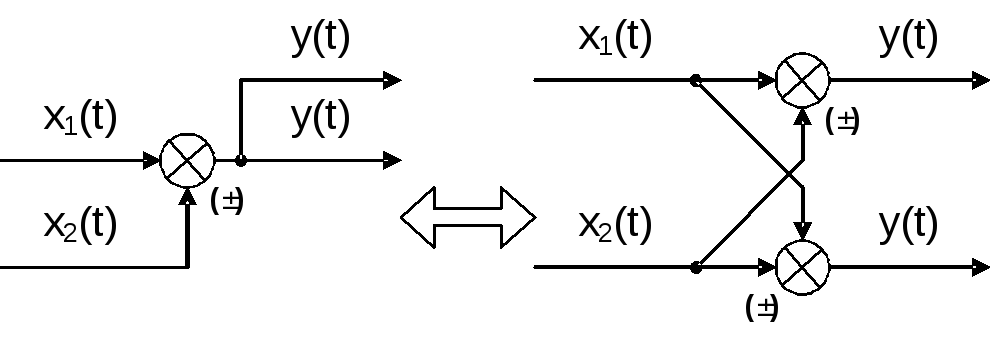
Это правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести сумматор через узел, необходимо в схему включить дополнительный сумматор. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х1(t) + х2(t).
-
Перенос сумматора через сумматор.

Это правило преобразования структурных схем фактически реализует правило коммутативности сложения в математике – от перестановки мест слагаемых сумма не изменяется. Оно, разумеется, применимо как к сумматорам, так и к элементам сравнения.
-
Перенос звена через звено.

Это правило преобразования структурных схем фактически реализует правило коммутативности умножения в математике – от перестановки мест множителей произведение не изменяется.
-
Перенос узла через узел.

Это правило настолько очевидно, что не имеет смысла его комментировать.
