Лекции по Теории автоматического управления (ТАУ) / ТАУ ЛЕКЦИЯ 12

Лекция 12.

Гармоническая линеаризация.

Назначение метода гармонической линеаризации.

Идея метода гармонической линеаризации была предложена в 1934г. Н. М. Крыловым и Н. Н. Боголюбовым. Применительно к системам автоматического управления этот метод разработан Л. С. Гольдфарбом и Е. П. Поповым. Другие названия этого ме­тода и его модификаций - метод гармонического баланса, метод описывающих функций, метод эквивалентной линеаризации.

Метод гармонической линеаризации - это метод исследова­ния автоколебаний. Он позволяет определять условия существования и параметры возможных автоколебаний в нелинейных си­стемах.

Знание параметров автоколебаний позволяет представить картину возможных процессов в системе и, в частности, определить условия устойчивости. Предположим, например, что в результате исследования автоколебаний в некоторой нелинейной системе мы получили зависимость амплитуды этих автоколебаний А от коэффициента передачи k линейной части системы, показанную на рис.12.1, и знаем, что автоколебания устойчивы.

Из графика следует, что при большом значении коэффициента передачи k, когда k > k_кр, в системе существуют автоколебания. Их амплитуда уменьшается до нуля при уменьшении коэффициента передачи k до k_кр. На рис.12.1 стрелками условно показан характер переходных процессов при разных значениях k: при k > k_кр переходный процесс, вызванный начальным отклонением, стягивается к автоколебаниям. Из рисунка видно, что при k < k_кр, система оказывается устойчивой. Таким образом, k_кр – это критическое по условию устойчивости значение коэффициента передачи. Его превышение приводит к тому, что исходный режим системы становится неустойчивым и в ней возникают автоколебания. Следовательно, знание условий существования автоколебаний в системе позволяет определить и условия устойчивости.

Идея гармонической линеаризации.

Рассмотрим нелинейную систему, схема которой представлена на рис.12.2, а. Система состоит из линейной части с передаточной функцией W_л (s) и нелинейного звена НЛ с конкретно заданной характеристикой . Звено с коэффициентом - 1 показывает, что обратная связь в системе отрицательна. Полагаем, что в системе существуют автоколебания, амплитуду и частоту которых мы хотим найти. В рассматриваемом режиме входная величина Х нелинейного звена и выходная Y являются периодическими функциями времени.

Метод гармонической линеаризации основан на nредnоложении, что колебания на входе нелинейного звена являются синусоидальны.ми, т. е. что

, (12.1)

где А – амплитуда и - частота этих автоколебаний , а - возможная в общем случае постоянная составляющая, когда автоколебания несимметричны.

В действительности автоколебания в нелинейных системах всегда несинусоидальны вследствие искажения их формы нели­нейным звеном. Поэтому указанное исходное предположение озна­чает, что метод гармонической линеаризации является принципиально приближенным и область его применения ограничена случаями, когда автоколебания на входе нели­нейного звена достаточно близки к синусоидальным. Для того чтобы это имело место, линейная часть системы должна не пропу­скать высших гармоник автоколебаний, т. е. являться фильтром нижних частот. Последнее иллюстрируется рис. 12.2, б. Если, например, частота автоколебаний равна , то линейная часть с показанной на рис. 12.2, б АЧХ будет играть роль фильтра нижних частот для этих колебаний, так как уже вторая гармоника, частота которой равна 2, практически не пройдет на вход нелинейного звена. Следовательно, в этом случае метод гармонической линеаризации применим.

Если частота автоколебаний равна , линейная часть будет свободно пропускать вторую, третью и другие гармоники автоколебаний. В этом случае нельзя утверждать, что колебания на входе нелинейного звена будут достаточно близки к синусоидальным, т.е. необходимая для применения метода гармонической линеаризации предпосылка не выполняется.

Для того чтобы установить, является ли линейная часть си­стемы фильтром нижних частот и тем самым определить примени­мость метода гармонической линеаризации, необходимо знать частоту автоколебаний. Однако ее можно узнать только в резуль­тате использования этого метода. Таким образом, пpимeнимocть метода гармонической лuнеарuзацuu прuходuтся определять уже в конце uсследованuя в порядке проверки.

Заметим при этом, что если в результате этой проверки гипо­теза о том, что линейная часть системы играет роль фильтра ниж­них частот, не подтверждается, это не означает еще неверности полученных результатов, хотя, разумеется, ставит их под сом­нение и требует дополнительной проверки каким-либо другим методом.

Итак, предположив, что линейная часть системы есть фильтр нижних частот, считаем, что автоколебания на входе нелинейного звена синусоидальны, т.е имеют вид (12.1). Колебания на выходе этого звена будут при этом уже несинусоидальными вследствие их искажения нелинейностью. В качестве примера на рис. 12.3 построена кривая на выходе нелинейного звена для определенной амплитуды входного чисто синусоидального сигнала по характеристике звена, приведенной там же.

Рис.12.3. Прохождение гармонического колебания через нелинейное звено.

Однако, поскольку мы считаем, что линейная часть системы пропускает только основную гармонику автоколебаний, имеет смысл интересоваться только этой гармоникой на выходе нелинейного звена. Поэтому разложим выходные колебания в ряд Фурье и отбросим высшие гармоники. В результате получим:

. (12.2)

Здесь

;

; (12.3)

;

.

Перепишем выражение (12.2) в более удобном для последующего использования виде, подставив в него получающиеся из (12.1) следующие выражения для и :

и .

Подставив эти выражения в (12.2), будем иметь:

(12.4)

или

. (12.5)

Здесь введены обозначения:

. (12.6)

Дифференциальное уравнение (12.5) справедливо для синусоидального входного сигнала (12.1) и определяет выходной сигнал нелинейного звена без учета высших гармоник.

Коэффициенты в соответствии с выражениями (12.3) для коэффициентов Фурье являются функциями постоянной составляющей , амплитуды А и частоты автоколебаний на входе нелинейного звена. При фиксированных А, и уравнение (12.5) является линейным. Таким образом, если отбросить высшие гармоники, то для фиксированного гармонического сигнала исходное нелинейное звено может быть заменено эквивалентным линейным, описываемым уравнением (12.5). Эта замена и называется гармонической линеаризацией.

На рис. 12.4 условно изображена схема этого звена, состоящая из двух параллельных звеньев.

Рис. 12.4. Эквивалентное линейное звено, полученное в результате гармонической линеаризации.

Одно звено () пропускает постоянную составляющую, а другое – только синусоидальную составляющую автоколебаний.

Коэффициенты называются коэффициентами гармонической линеаризации или гармоническими коэффициентами передачи: - коэффициент передачи постоянной составляющей, а - два коэффициента передачи синусоидальной составляющей автоколебаний. Эти коэффициенты определяются нелинейностью и значениями и по формулам (12.3). Существуют определенные по этим формулам готовые выра­жения для для ряда типовых нелинейных звеньев. Для этих и вообще всех безынерционных нелинейных звеньев вели­чины не зависят от и являются функциями только амплитуды А и .

Постоянная составляющая на выходе нелинейного звена (см. уравнения 12.2, 12.4) появляется по одной из двух причин: если к системе приложено внешнее постоянное воздействие, создающее (см. уравнение 12.1), или если характеристика нелинейного звена несимметрична относительно начала коорди­нат, вследствие чего происходит явление выпрямления входного синусоидального сигнала.

При гармонической линеаризации нелинейных звеньев с такими характеристиками нельзя выражать через с помощью коэф­фициента гармонической линеаризации , т. е. в виде

,

так как здесь и при . Поэтому для несимметричных нелинейностей нельзя пользоваться уравнением (12.5), а следует применять уравнение (12.4). Соответствующая схема представлена на рис. 12.4,б. В связи с этим для таких нелинейностей вместо даются выражения непосредственно для .

При отсутствии внешнего воздействия и симметричной харак­теристике постоянная составляющая и уравнение (12.4) принимает вид:

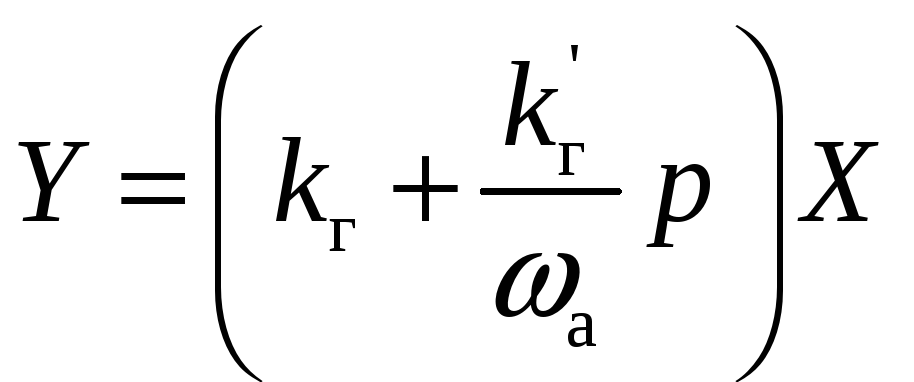(12.7)

или

, (12.8)

где - передаточная функция эквивалентного линейного звена, которую можно назвать гармонической передаточной функцией нелинейного звена.

Итак, при гармонической линеаризации, нелинейное звено заменяется линейным, эквивалентным для постоянной составляющей входного сигнала и приближенно эквивалентным для его колебательной составляющей. При этом приближенно принимается, что спектр колебательной составляющей входного сигнала состоит из одной гармоники, и пренебрегается ее искажением в нелинейном звене.

Условием применимости метода линеаризации в замкнутой системе является выполнение линейной частью системы роли фильтра нижних частот. Полоса пропускания должна быть мала по сравнению с высшими гармониками автоколебаний.

С помощью гармонической линеаризации можно определить параметры возможных автоколебаний в интересующей нас точке системы, которые могут быть использованы для определения устойчивости нелинейной системы, качества переходных процессов.

Особенности коррекции динамических свойств нелинейных систем.

Как и у линейных САУ, коррекция динамических свойств нелинейных систем осуществляется с помощью корректирующих звеньев. Эти звенья могут быть линейными и нелинейными. Линей­ные корректирующие звенья были рассмотрены ранее. Все изложенное там о них в полной мере справедливо и в случае применения этих звеньев для коррекции нелинейных САУ.

Здесь мы остановимся на принципиально новых возможностях, которые возникают при применении с целью коррекции динами­ческих свойств системы нелинейных звеньев.

Первым, наиболее очевидным случаем, когда целесообразно использование нелинейных корректирующих звеньев, является применение их для устранения или уменьшения отрицательного влияния на работу системы какой-либо входящей в нее нежела­тельной нелинейности. Например, с помощью звена со специально подобранной нелинейной статической характеристикой может быть выровнена или вообще нужным образом деформирована стати­ческая характеристика всей САУ в целом. Другой пример ­уменьшение влияния насыщения, которое часто имеет место, особенно в исполнительных звеньях САУ. Насыщение в стати­ческих характеристиках этих звеньев приводит к сильному затя­гиванию переходных процессов, т. е. к снижению быстродействия системы, при больших внешних воздействиях. В этих случаях можно добиться значительного ускорения переходных процессов, если линейные корректирующие звенья, создающие форсирующие воздействия, заменить или дополнить нелинейными звеньями, которые затягивали бы форсировку, задерживая исполнительный сигнал на предельно возможном с учетом насыщения значении. Для получения макси­мального быстродействия при наличии ограничений переменных управление должно быть нелинейным, а именно - релейным.

Нелинейная коррекция позволяет повышать качество САУ, в том числе и линейных, с получением результатов совершенно недостижимых средствами линейной коррекции. Например, с помощью введения нелинейной коррекции в чисто линейную САУ можно устранить известное противоречие между быстродействием и колебательностью, обеспечив возможность независимого выполнения требований по каждому из этих показателей.

Нелинейные корректирующие звенья.

Нелинейные корректирующие звенья бывают двух типов: не­линейные корректирующие звенья, включаемые последовательно или параллельно с основными звеньями системы, и переключаю­щие корректирующие звенья, релейно изменяющие настройку или структурную схему системы при соответствующем изменении ее состояния или внешних условий. Последний тип корректирующих звеньев присущ только нелинейной коррекции.

В качестве нелинейных корректирующих звеньев применяются нелинейные звенья непрерывного и дискретного действия, их комбинации друг с другом, а также с линейными корректирующими звеньями.

Простейшим видом нелинейных корректирующих звеньев являются корректирующие звенья с нелинейными статическими характеристиками. Первая область их применения, как уже говорилось, - это кор­рекция статических характеристик системы и, в частности, кор­рекция нежелательных нелинейностей ее основных звеньев. Вторая область применения – это коррекция динамических свойств. В этом случае такие безынерционные корректирующие звенья часто применяются в комбинации с линейными корректирующими звеньями, образуя вместе нелинейные динамические корректирующие звенья.

В качестве нелинейных статических характеристик используют при этом характеристики с насыщением, зоной нечувствительности, петлевые, а также различные специально подобран­ные нелинейности. Если пользоваться частотным описанием таких нелинейных динамических корректирующих звеньев (на основе гармонической линеаризации), то их назначение можно опреде­лить следующим образом. Во-первых, они применяются для получения определенной желаемой зависимости частотных харак­теристик от амплитуды сигнала и тем самым для получения раз­личной реакции системы на воздействия разной величины или, наоборот, для устранения нежелательных таких зависимостей, обусловленных имеющимися в системе нелинейностями основных звеньев. Во-вторых, такие корректирующие звенья применяются для преодоления той жесткой зависимости между амплитудной и фазовой частотными характеристиками, которая существует в ли­нейных системах, с целью независимой корректировки каждой из этих характеристик. Для последней цели часто используются так называемые псевдолинейные корректирующие звенья.

Рис.12.5. Структурная схема нелинейного динамического корректирующего звена.

На рис. 12.5 в качестве примера показана структурная схема нелинейного динамического корректирующего звена, состоящего из двух линейных корректирующих звеньев 1 и 3 и нелинейного звена с насыщением 2. При звено 1 является обычным пропорционально-дифференцирующим звеном, т. е. фильтром верх­них частот, а звено 3 - соответственно инерционным звеном, т. е. фильтром нижних частот. Для малых входных сигналов, когда нелинейное звено 2 не входит в насыщение, передаточная функция всей схемы равна 1, т. е. это звено не влияет на работу си­стемы, в которой находится. При достаточно больших сигналах, когда звено 2 входит в насыщение, схема ведет себя как динами­ческое звено со спадающей с ростом частоты амплитудной частот­ной характеристикой, степень спадания которой зависит от вели­чины входного сигнала, и с примерно постоянным фазовым сдвигом.

Такое корректирующее звено применяется в качестве последо­вательного корректирующего звена, например, для устранения автоколебаний при больших возмущениях и соответствующего увеличения критического по устойчивости значения коэффициента передачи системы. Это корректирующее звено применяется также в цепях обратной связи, например, следящих систем для улуч­шения качества переходных процессов при больших входных сигналах.

Псевдолинейные корректирующие звенья – это нелинейные корректирующие звенья, эквивалентные амплитудные и фазовые частотные характеристики которых не зависят от амплитуды входного сигнала, чем и объясняется их название. Как уже говорилось, основным свойством этой группы корректирующих звеньев является практическое отсутствие связи между эквивалентными амплитудной и фазовой частотными характеристиками.

Существуют два основных типа псевдолинейных корректирую­щих звеньев: фильтры с амплитудным ослаблением - для коррек­ции амплитудной характеристики без изменения фазы и фильтры с фазовым опережением - для коррекции фазовой характеристики без изменения амплитудной характеристики.

На рис. 12.6 показан пример схемы фильтра с амплитудным ослаблением. Здесь звено 1 - реле, 2 - фильтр нижних частот ФНЧ, звено 3 дает абсолютное значение (модуль) входного сиг­нала Х₁ (в электрических системах постоянного тока это выпрямительная схема), 4 – множительное звено.

Рис.12.6. Схема нелинейного фильтра с амплитудным ослаблением.

Существует много других псевдолинейных корректирующих устройств. Имеются, например, псевдолинейные интегрирующие звенья, амплитудная характе­ристика которых совпадает с амплитудной характеристикой обыч­нoгo линейного интегрирующего звена, а фазовый сдвиг вдвое меньше, что облегчает задачу стабилизации астатических систем с таким интегрирующим звеном. Предложены псевдолинейные дифференцирующие звенья, обладающие характеристиками, более близкими к характеристикам идеального дифференцирующего звена, чем у реальных линейных дифференцирующих звеньев.

Сложные нелинейные динамические корректирующие звенья получаются в результате синтеза оптимальных САУ. Они включают, помимо функциональных зависимо­стей, логические операции и зачастую требуют для своей реали­зации специального вычислительного устройства.

Переключающие корректирующие зве­нья осуществляют коррекцию динамических свойств системы путем дискретных изменений ее параметров и структурной схемы в ходе процесса управления в функции переменных системы и внешних воздействий. Эти изменения могут осуществляться как в основных, так и в корректирующих звеньях системы.

Примером такой коррекции является релей­ная форсировка переходных процессов в системах с насыщением, которая осуществляется при больших отклонениях от заданного режима путем дискретного изменения настройки корректирую­щих звеньев системы.

Переключающие корректирующие звенья применяются также для изменения алгоритма работы управляющего устройства си­стемы при значительных изменениях внешних условий или свойств самой системы. Системы с такой коррекцией относятся к простей­шим самоорганизующимся САУ.

В системах, управляющее устройство которых включает в себя вычислительную машину, реализующую алгоритм управления, переключающие корректирующие звенья часто также могут быть реализованы алгоритмически в этой ЭВМ без создания их физи­чески в виде отдельного функционального блока.

Изложенное показывает большие возможности нелинейной коррекции. Вместе с тем, говоря о достоинствах нелинейной кор­рекции, следует отметить, что такая коррекция по своей природе является более специализированной по отношению к режимам системы, при которых она дает нужный эффект. Может получиться, например, так, что нелинейная коррекция, выбранная для опре­деленного вида внешних воздействий, окажется не только неэф­фективной, но даже вредной при других неучтенных режимах САУ. Поэтому, чем шире диапазон внешних воздействий и вообще усло­вий работы системы, тем труднее выбрать нелинейную коррекцию и тем скорее может оказаться наиболее приемлемой линейная кор­рекция. Последнее обстоятельство усугубляется тем, что, к сожа­лению, не существует какой-либо общей методики выбора нели­нейных корректирующих звеньев и практически при синтезе приходится прибегать к методу проб и последовательных при­ближений, используя опыт и известные рекомендации по приме­нению отдельных частных приемов и схем нелинейной коррекции.

9