Лекции по Теории автоматического управления (ТАУ) / ТАУ ЛЕКЦИЯ 11

ЛЕКЦИЯ 11

НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

К нелинейным системам автоматического управления относятся такие системы, в которых связь между выходной и входной величинами одного или нескольких основных элементов задается нелинейными уравнениями.

В общем случае каждая система автоматического управления имеет те или иные нелинейности, однако часто эти нелинейности влияют столь незначитель­но, что поведение системы с достаточной точностью может быть описано только линейными дифференциальными уравнениями. Нелинейные уравнения про­цессов в такой системе заменяют приближенными линейными уравнениями и исследуют систему как линейную.

Вопрос о возможности линеаризации уравнений или процессов в системе решают исходя из требования точности расчетов. Часто решение этого вопроса зависит от того, при каких отклонениях переменных величин работает система.

Одну и ту же систему в зависимости от конкретных условий работы, а также от принятой степени идеализации процессов, протекающих в ней, можно рассматривать как линей­ную и как нелинейную. Однако какие же системы в теории автоматического управления относятся к нелинейным? Это такие системы, которые нельзя рассматривать как линейные даже при малых отклонениях переменных, иначе говоря, такие системы, которые име­ют существенно нелинейные характе­ристики.

Сущесmвенно нелинейными называ­ются такие характеристики, которые в некоторых тачках рабочего интервала неоднозначны, терпят разрыв или во­обще не существуют.

Системы с существенно нелинейны­ми элементами линеаризовать методами, рассмотренными при рассмотрении линейных систем, невозможно. Если ограничиться линеаризацией в тех точках, где она допу­стима, и попытаться анализировать систему как линейную во всем рабочем диапазоне, то можно получить неверные результаты.

Нелинейные системы классифицируют по виду существенно нелинейных элементов, входящих в систему. Следовательно, классификация нелинейных систем сводится к классификации существенно нелинейных характеристик элементов.

Существенно нелинейных характеристик много. Рассмотрим наиболее часто встречающиеся из них.

Ограниченно-линейные характеристики линейные (наклонные) в начале и нелинейные (горизонтальные) по краям (рис.11.1). Такую характеристику имеют уси­лители и, в частности, электронный усилитель. Поскольку нали­чие нелинейных участков связано с насыщением элементов усилителей, то часто эту характеристику называют характеристикой с зоной насыщения.

Рис.11.1. Статическая характеристика электронного усилителя.

Характеристики с зоной нечувствительности. Если на вход элемента, имею­щего характеристику с зоной нечувствительности, подавать сигнал х₁, то до тех пор, пока этот сигнал не превысит некоторого порогового значения х₁₀, выходной сигнал х₂ будет равен нулю (рис.11.2,а). Пороговые значения входной величины разных знаков определяют величину зоны нечувствительности (на рис. 11.2,а зона нечувствительности равна 2x₁₀).

Рис.11.2. К определению характеристики с зоной нечувствительности.

Появление зоны нечувствительности может быть вызвано различными при­чинами, зависящими от конструктивного выполнения и принципа действия данного элемента.

Например, в характеристике золотника причиной появления зоны нечувст­вительности является конструктивная особенность поясков поршня (рис.11.2,б). Поскольку ширина поясков больше, чем ширина отверстий, через которые мас­ло поступает в гидропривод, то понадобится осуществить некоторое· переме­щение штока золотника, прежде чем отверстия начнут открываться, и масло будет поступать в ту или другую полость гидропривода. Если характеристику с зоной нечувствительности (рис.11.2,а) отнести к золотнику, то х₁ будет обозначать ход штока золотника, а х₂ – количество масла, проходящего через отверстие в единицу времени. В этом случае величина х₂ определяет скорость движения поршня гидропривода.

На рис.11.2,в представлен другой элемент, характеристика которого имеет зону нечувствительности,- устройство для передачи колебаний оси х₁ на маят­ник с помощью поводка. Так как вилка имеет раствор δ, больший диаметра d подвески маятника, то приводная ось будет иметь свободный ход, при котором маятник остается в нулевом положении. Очевидно, что величина зоны нечувст­вительности равна δ - d.

Характеристики типа сухого трения или зазора имеют вид петли. Они не­однозначны во всем диапазоне изменения входной величины х₁ (рис.11.3,а). Поясним построение такой характеристики на примере передачи угла поворота с помощью поводка и вилки (рис.11.3,б).

Пусть с оси 1 на ось 2 требуется передать угол поворота х₁. С этой целью на оси 1 имеется вилка с раствором δ, а на оси 2 - поводок с диаметром d. Если вилка касается поводка стороной, противоположной направлению вращения, то угол поворота х₂ изменяется пропорционально углу поворота х₁. При изме­нении направления вращения вилка должна коснуться поводка другой сторо­ной. Следовательно, ось 1 будет иметь свободный ход, во время которого в передаче выбирается зазор δ - d, а ось 2 остается в неизменном положении.

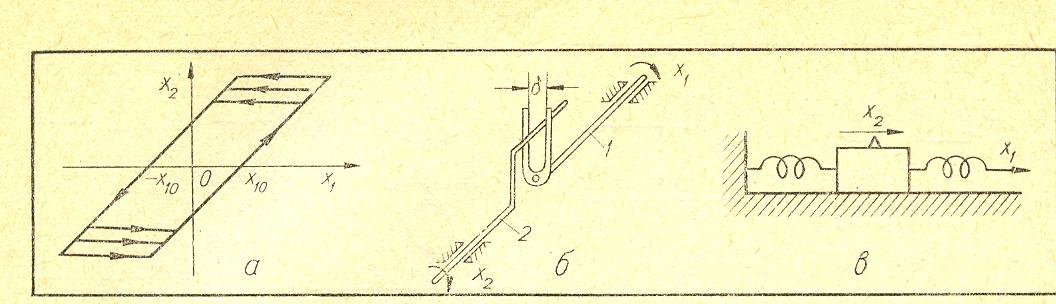
Рис.11.3. К определению характеристики типа сухого трения или зазора.

Такую же характеристику имеет устройство, в котором осуществляется перемещение х₂ ползунка по направляющей под действием перемещения х₁ свободного конца пружины (рис.11.3,в). При перемене направления движения сила трения F_тр, действующая между ползунком и направляющей, изменяет свой знак. Поэтому ползунок остается в неизменном положении до тех пор, пока сила, действующая на пружину, не уменьшится на величину 2 F_тр.

Сухое трение и зазоры, давая одинаковые по внешнему виду нелинейные характеристики элементов, принципиально отличаются друг от друга тем, что зазор в системе можно свести к нулю, например, установкой предварительно затянутой спиральной пружины на ось 2 (рис. 11.3,б), а силу трения можно только уменьшить, но к нулю свести ее нельзя.

Релейные характеристики имеют ту отличительную особенность, что в них при достижении входной величиной некоторых пороговых значений выходная величина изменяется скачкообразно (рис.11.4 – 11.7).

Рис.11.4. Схема включения (а) и Рис. 11.5. Схема включения (а) и характеристика (б,в) скользя-

характеристика (б) эле- щего контакта.

ктрического контакта.

Рис. 11.6. Характеристика электро- Рис. 11.7. Схема включения (а) и характеристика (б) биметал-

магнитного реле. лического (теплового) реле.

Например, электрический контакт в зависимости от угла поворота произво­дит подачу напряжения в исполнительную цепь (рис. 11.4,а). Контакт имеет холостой ход х₁₀ (рис. 11.4,б). При х₁ ≥ х₁₀ в исполнительную цепь подается напряжение .

У скользящего контакта, который управляет вращением реверсивного электродвигателя, положение щетки шириной d на контактной пластине опре­деляется углом поворота х₁ рычага щеткодержателя (рис. 11.5, а). Контактная пластина имеет в своей средней части изоляционный участок шириной δ. На­пряжение подается на ту или иную обмотку электродвигателя в зависимости от того, на каком проводящем участке пластины находится щетка. На рис. 11.5, б и в приведены характеристики скользящего контакта для случаев соответствен­но d = δ и d < δ. На характеристиках через х₂ обозначена скорость вращения электродвигателя.

На рис. 11.6 изображена типичная характеристика электромагнитного реле (х₁ – ток в обмотке реле или напряжение, подаваемое на обмотку; х₂ - ход контактов, отсчитываемый от их нормального положения). Характеристика имеет петлю, ширина которой равна разности тока срабатывания и тока отпу­скания.

На рис. 11.7,а изображено биметаллическое (тепловое) реле, управляющее исполни­тельным реверсивным электродвигателем. Реле имеет в качестве чувствитель­ного элемента биметаллическую пластину, помещенную между двумя непо­движными шарнирами. При некоторой температуре пластина изогнута так, что замкнут левый контакт. По мере уменьшения температуры пластина будет стремиться изогнуться в противоположную сторону. Перебрасывание контакта, а следовательно, и реверс двигателя может произойти только при температуре, ниже той, при которой кривизна свободной пластинки равна нулю. Характе­ристика реле изображена на рис. 11.7, б, где по оси абсцисс отложены изменения температуры х₁, а по оси ординат - скорость вращения х₂ электродвигателя.

Следует отметить, что не все системы, имеющие контакты, относятся к не­линейным. В автоматических системах могут использоваться различные реле вспомогательного характера (например, для подключения источников питания), скачкообразность изменения выходных величин которых не влияет су­щественно на характер процесса управления. Такие системы можно отнести к линейным, если только у них нет других нелинейных элементов.

Нелинейная характеристика, имеющая вид петли гистерезиса, изображена на рис. 11.8. При наличии гистерезиса, например магнитного или механическо­го, зависимость выходной величины от входной будет неоднозначной. В отдель­ных случаях при точных расчетах эту неоднозначность приходится учитывать. Однако чаще при расчетах усредняют характеристику, заменяя петлю некото­рой средней линией. Так поступают, например, при использовании кривых на­магничивания различных сортов стали или при использовании характеристик механических пружин. В этом случае характеристика будет плавной, т. е. несущественно нелинейной.

Рис.11.8. Гистерезисная характери- Рис.11.9. Схема (а) и характеристика (б) пневматического

стика. усилителя.

Комбинированные нелинейные характеристики представляют собой ком­бинацию из различных характеристик, рассмотренных ранее.

Примером может служить характеристика пневматического усилителя, который применяют в различных автоматических устройствах и, в частности, в ав­топилотах. Рассмотрим принцип действия этого усилителя (рис. 11.9,а). К за­дающим соплам 3 и 4, против которых расположены приемные сопла 1 и 5, подводится воздух под некоторым давлением. Приемные и задающие сопла разделены заслонкой 2, которая может поворачиваться относительно оси 00', изменяя степень перекрытия приемных сопел. В результате этого давления в камерах пневматического реле 6 будут различными, что вызовет прогиб мембра­ны реле в ту или иную сторону.

Входной величиной усилителя является угол поворота заслонки х₁, а вы­ходной - ход штока, связанного с мембраной пневматического реле х₂. Если в исходном положении оба сопла закрыты, то заслонка должна повернуться на некоторый угол х₁₀, прежде чем одно из сопел начнет воспринимать давление (рис. 11.9,б). При повороте заслонки на угол x₁₀ ≤ х₁ ≤ х₁₁ разность давлений в камерах пневматического реле, а следовательно, и перемещение штока х₂ будут пропорциональны углу поворота заслонки. Когда одно из приемных сопел полностью открыто (х₁ > х₁₁), в пневматическом реле установится максималь­ный перепад давления, который будет оставаться постоянным при дальнейшем повороте заслонки.

Как видно из рис. 11.9,б, характеристика пневматического усилителя яв­ляется комбинацией ограниченно-линейной характеристики и характеристики с зоной нечувствительности.

В чем характерное отличие нелинейных элементов от линейных с точки зрения теории автоматического управления?

1. Выходная величина нелинейной системы непропорциональна входному воздействию; форма реакции системы зависит от величины входного воздействия.

2. Характер процессов в нелинейной системе зависит от величины начального отклонения, вызванного возмущением. В связи с этим для нелинейных систем существуют понятия об устойчивости “в малом”, “в большом”, “в целом”.

3. Для нелинейных систем характерен режим незатухающих периодических колебаний с постоянной амплитудой и частотой (автоколебаний), возникающий в системах при отсутствии периодических внешних воздействий.

4. При затухающих колебаниях переходного процесса в нелинейных системах происходит изменение периода колебаний.

Основные задачи исследования нелинейных систем. Методы исследования. Задачами исследования нелинейных систем являются:

1) отыскание возможных состояний равновесия системы и исследование их устойчивости;

2) определение автоколебаний и анализ их устойчивости;

3) исследование процессов перехода системы к тому или иному установившемуся состоянию при различных начальных отклонениях.

Начало исследования нелинейных систем обычно связано с рассмотрением устойчивости и определением автоколебаний.

В настоящее время не создано общей теории анализа нелинейных систем. Разработанные методы позволяют решать лишь отдельные нелинейные задачи.

Все инженерные методы исследования нелинейных систем разделяются на две основные группы.

Точные методы, например, метод А.М.Ляпунова, метод фазовой плоскости, метод точечных преобразований, частотный метод В.М.Попова, основаны на точном решении нелинейного дифференциального уравнения, может быть и упрощенного.

Приближенные методы, такие как метод гармонической линеаризации, метод статистической линеаризации, основаны на линеаризации нелинейного уравнения системы.

Мощным и эффективным методом исследования нелинейных систем является моделирование, инструментарием которого служит компьютер. В настоящее время многие сложные для аналитического решения теоретические и практические вопросы сравнительно легко могут быть решены с помощью вычислительной техники.

Особенности динамики нелинейных систем.

В отличие от линейных систем точ­ность нелинейных систем зависит от величины внешних воздей­ствий. Такая же зависимость существует и в отношении устойчи­вости и качества переходных процессов в нелинейных системах.

У линейных систем точность, устойчивость и качество переходных процессов не за­висят от величины внешних воздействий. Благодаря применимости к линейным системам принципа суперпозиции изменение величины внeшнего воздействия вызывает в них только пропорциональное изменение абсолютного отклонения выходной величины, не ска­зываясь на качестве переходного процесса (его колебательности, длительности). Последнее иллюстрируется рис. 11.10,а, где приве­дены переходные характеристики для трех значений внешнего воздействия, пропорциональных числам, которыми отмечены харак­теристики.

Устойчивость линейных САУ вообще не зависит от внешних воздействий и определяется параметрами самой системы. Если линейная система устойчива, то это значит, что она устойчива относительно любого установившегося режима и переходная составляющая любого процесса всегда будет сходящейся.

Рис. 11.10. К особенностям динамики нелинейных систем.

В нелинейных системах дело обстоит сложнее. Качество пере­ходных процессов в них изменяется при изменении величины внешнего воздействия, например, как показано на рис.11.10,б. При этом в отличие от линейных систем период колебаний процес­са не постоянен, а изменяется по мере изменения отклонения. (Чаще всего он уменьшается с уменьшением отклонения – см. рис.11.10,б). Более того, нелинейная система, устойчивая при одних значениях внешних воздействий, может оказаться неустойчивой с возникновением расходящегося переходного процесса при других значениях этого воздействия (рис.11.10,в и г).

На рис.11.10, в показан случай, когда система, устойчивая при малых воздействиях (кривая 1), неустойчива при больших воз­действиях с получением колебательного (кривая 2) или моно­тонного (кривая 3) расходящегося переходного процесса. На рис.11.10, г представлен другой случай, когда, наоборот, при малых возмущениях переходный процесс является расходящимся (кри­вая 1), а при больших - затухающим (кривая 2). В этом случае, очевидно, установившимся режимом при отсутствии внешних воздействий будут незатухающие колебания (кривые 3). После всякого воздействия, сбивающего эти колебания к нулю, в системе будет возникать расходящийся процесс их восстановления, а после всякого воздействия, создающего большое отклонение выходной величины, будет возникать процесс, сходящийся опять к этим колебаниям.

Возможной причиной получения случая, показанного на рис.11.10, в, может быть, например, наличие насыщения в корректи­рующем звене, обеспечивающем устойчивость системы, а причиной второго случая, показанного на рис.11.10, г, - наличие зоны нечувствительности у этого же звена. Здесь в первом случае неустойчивость возникает при больших отклонениях от установив­шегося режима вследствие ослабления действия корректирующего звена из-за его насыщения. Во втором случае неустойчивость будет в точке покоя, поскольку при малых отклонениях относи­тельно этой точки коррекция не действует из-за наличия зоны нечувствительности. При больших отклонениях корректирующее звено выходит из зоны нечувствительности и обеспечивает зату­хающий переходный процесс вхождения обратно в эту зону. В установившемся состоянии, следовательно, в системе будут существовать незатухающие колебания, амплитуда которых огра­ничена зоной нечувствительности, несколько превышая ее.

Такие устойчивые собственные колебания с постоянной ампли­тудой, определяемой нелинейностями системы, называются а в т о ­к о л е б а н и я м и. Автоколебания представляют собой новый вид установившегося режима, возможного при отсутствии внешних воздействий наряду со статическим установившимся режимом и характерного только для нелинейных систем. В линейных си­стемах, как мы знаем, собственные незатухающие колебания могут быть при нахождении системы на границе устойчивости, однако амплитуда этих колебаний определяется внешними воздействиями, будучи пропорциональна им. При этом такая линейная САУ является неработоспособной.

Если же в нелинейной САУ возможны автоколебания, то это еще не означает, что она непригодна к эксплуатации. Во-первых, эти автоколебания могут быть настолько малы по амплитуде, что не будут оказывать заметного влияния на работу системы. Это часто относится, например, к автоколебаниям, вызываемым нали­чием зоны нечувствительности. Во-вторых, может быть другой случай, когда в системе принципиально возможны автоколебания с большой амплитудой, однако, для того, чтобы они возникли, требуется соответственно очень большой внешний толчок. В ре­зультате может оказаться, что при всех практически возможных воздействиях на систему в ней могут быть только устойчивые переходные процессы. Этот случай соответствует кривым 1 и 2 на рис.11.10, в, если предположить, что кривая 2 расходится не до бесконечности, а до автоколебаний с определенной амплитудой. Подобный случай может быть, например, если наряду с насыще­нием корректирующего звена, приводящим при больших воздей­ствиях к нарушению устойчивости с переходом от кривой 1 к кривой 2, в системе имеется еще другое последовательное звено с насыщением на значительно большем уровне, которое и ограни­чивает амплитуду колебаний кривой 2.

Возможны нелинейные системы, в которых в зависимости от велич:ины внешних воздействий возникают разные автоколебания, с разными амплитудами и частотами. Это иллюстрируется рис.11.10, д. Здесь при малых воздействиях переходные процессы стягиваются к автоколебаниям с амплитудой А₁, а при больших - к авто­колебаниям с амплитудой А₂ (моменты времени t₁ и t₂ - начала соответствующих переходных процессов).

Описанные особенности устойчивости нелинейных систем тре­буют при рассмотрении устойчивости таких систем оговаривать начальные условия и внешние воздействия, как это делалось ранее при рассмотрении качества линейных систем. В результате в слу­чае нелинейных систем надо говорить не об устойчивости системы вообще, а об устойчивости определенного ее статического или динамического режима, т. е. определенного ее состояния или дви­жения при определенных отклонениях от него. В связи с этим при изучении нелинейных систем употребляются понятия устой­чивости в малом, в большом и в целом.

У с т о й ч и в о с т ь в м а л о м - это устойчивость при бесконечно малых отклонениях от исходного режима.

У с т о й ­ч и в о с т ь в б о л ь ш о м - это устойчивость при конечных отклонениях, возможных в данной системе по условиям ее работы.

У с т о й ч и в о с т ь в ц е л о м - это устойчивость при неогра­ниченных отклонениях, т. е. при отсутствии каких-либо ограниче­ний их. Нелинейная система может быть устойчива в малом, но неустойчива в большом (рис.11.10,в). В линейных системах таких градаций устойчивости не существует, там система либо неустой­чива, либо устойчива в целом. При этом в последнем случае будут устойчивы не только положения равновесия системы, но и любые вынужденные процессы.

9