- •230115 «Программирование в компьютерных системах»
- •1. Правило произведения
- •2. Правило суммы
- •3. Комбинаторный метод вычисления вероятностей
- •Равномерный закон распределения
- •Показательный закон распределения
- •Нормальный (гауссовский) закон распределения
- •Точечные оценки параметров
- •Точечные оценки m[X], d[X] и их свойства
- •Методы получения Точечных оценок
- •Интервальные оценки (доверительные интервалы)
- •Общие понятия теории графов
- •Сети, потоки в сетях. Теорема Форда – Фалкерсона
- •Процесс гибели – размножения и циклический процесс.
Нормальный (гауссовский) закон распределения
Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко
показать, что параметры
![]() и
и
![]() ,
входящие в плотность распределения
являются соответственно математическим
ожиданием и средним квадратическим
отклонением случайной величины Х.
,
входящие в плотность распределения
являются соответственно математическим
ожиданием и средним квадратическим
отклонением случайной величины Х.
Найдем функцию распределения F(x).
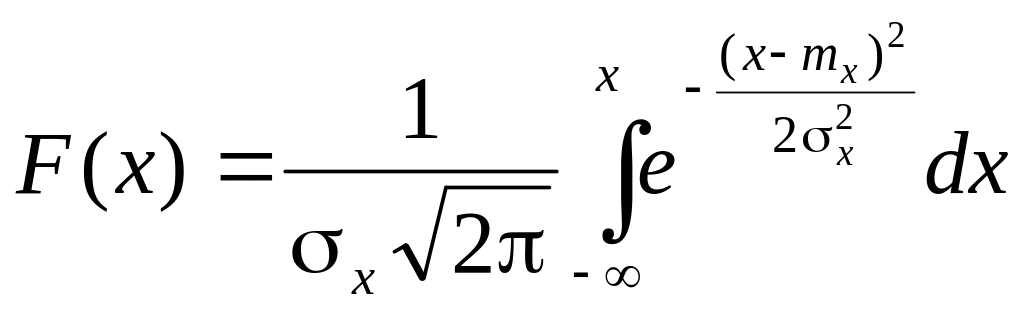
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4) Найдем экстремум функции.

Т.к. при y’
> 0 при x
< m
и y’
< 0 при x
> m
, то в точке х
= т функция
имеет максимум, равный
![]() .
.
5) Функция является симметричной относительно прямой х = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.

При x = m + и x = m - вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.
В этих точках
значение функции равно
![]() .
.
Построим график функции плотности распределения.

Построены графики при т =0 и трех возможных значениях среднего квадратичного отклонения = 1, = 2 и = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается..
Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.
При а
= 0 и
= 1 кривая называется нормированной.
Уравнение нормированной кривой:
![]()
Для краткости
говорят, что СВ Х подчиняется закону
N(m,
),
т.е. Х
N(m,
).
Параметры m
и
совпадают с основными характеристиками
распределения: m
= mX,
= Х
=
![]() .
Если СВ Х
N(0,
1), то она называется стандартизованной
нормальной величиной.
ФР стандартизованной нормальной
величиной называется функцией
Лапласа и
обозначается как Ф(x).
С ее помощью можно вычислять интервальные
вероятности для нормального распределения
N(m,
):
.
Если СВ Х
N(0,
1), то она называется стандартизованной
нормальной величиной.
ФР стандартизованной нормальной
величиной называется функцией
Лапласа и
обозначается как Ф(x).
С ее помощью можно вычислять интервальные
вероятности для нормального распределения
N(m,
):
P(x1
X
x2)
= Ф![]() - Ф
- Ф![]() .
.
При решении задач на нормальное распределение часто требуется использовать табличные значения функции Лапласа. Поскольку для функции Лапласа справедливо соотношение Ф(-х) = 1 - Ф(х), то достаточно иметь табличные значения функции Ф(х) только для положительных значений аргумента.
Для вероятности попадания на симметричный относительно математического ожидания интервал справедлива формула: P( X - mX ) = 2Ф(/) - 1.
Центральные моменты нормального распределения удовлетворяют рекуррентному соотношению: n+2 = (n+1)2n, n = 1, 2, ... . Отсюда следует, что все центральные моменты нечетного порядка равны нулю (так как 1 = 0).
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.
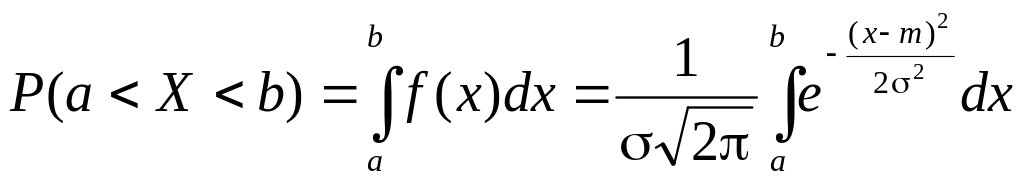
Обозначим
![]()
Тогда
![]()
Т.к. интеграл
![]() не выражается через элементарные
функции, то вводится в рассмотрение
функция
не выражается через элементарные
функции, то вводится в рассмотрение
функция
![]() ,
,
которая называется функцией Лапласа или интегралом вероятностей.
Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.
Ниже показан график функции Лапласа.

Функция Лапласа обладает следующими свойствами:
1) Ф(0) = 0;
2) Ф(-х) = - Ф(х);
3) Ф() = 1.
Функцию Лапласа также называют функцией ошибок и обозначают erf x.
Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:
![]()
Ниже показан график нормированной функции Лапласа.

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины :
![]()
Если принять = 3, то получаем с использованием таблиц значений функции Лапласа:
![]()
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (10065 = 6500) не превосходит 6600 – 6500 = 100 т.
Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.
Получаем:
![]()
Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.
Плотность распределения имеет вид:
![]()
Построим график:

Найдем вероятность попадания случайной величины в интервал (1; 3).
![]()
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.
![]()
Тот же результат может быть получен с использованием нормированной функции Лапласа.
![]()
Лекция 8 Закон больших чисел (Раздел 2)
План лекции
Центральная предельная теорема ( общая формулировка и частная формулировка для независимых одинаково распределенных случайных величин).
Неравенство Чебышева.
Закон больших чисел в форме Чебышева.
Понятие частоты события.
Статистическое понимание вероятности.
Закон больших чисел в форме Бернулли.
Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачивает случайный характер и становится закономерным (иначе говоря, случайные отклонения от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем, называемой законом больших чисел.
ЗАКОН БОЛЬШИХ ЧИСЕЛ – общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Первым примером действия этого принципа может служить сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (часто использующееся на практике, например, при использовании частоты встречаемости какого-либо качества респондента в выборке как выборочной оценки соответствующей вероятности).
Сущность закона больших чисел состоит в том , что при большом числе независимых опытов частота появления какого-то события близка к его вероятности.
Центральная
предельная теорема (ЦПТ) ( в формулировке
Ляпунова А.М. для одинаково распределенных
СВ). Если
попарно независимые СВ X1,
X2,
..., Xn,
... имеют одинаковый закон распределения
с конечными числовыми характеристиками
M[Xi]
=
и D[Xi]
= 2,
то при n
закон распределения СВ
![]() неограниченно приближается к нормальному
закону N(n,
неограниченно приближается к нормальному
закону N(n,
![]() ).
).
Следствие.
Если в условии теоремы СВ
![]() ,
то при n
закон распределения СВ Y
неограниченно приближается к нормальному
закону N(,
/
,
то при n
закон распределения СВ Y
неограниченно приближается к нормальному
закону N(,
/![]() ).
).
Теорема
Муавра-Лапласа. Пусть
СВ К - число “успехов” в n
испытаниях по схеме Бернулли. Тогда при
n
и фиксированном значении вероятности
“успеха” в одном испытании p
закон распределения СВ K
неограниченно приближается к нормальному
закону N(np,
![]() ).
).
Следствие.
Если в условии теоремы вместо СВ К
рассмотреть СВ К/n
- частоту “успехов” в n
испытаниях по схеме Бернулли, то ее
закон распределения при n
и фиксированном значении p
неограниченно приближается к нормальному
закону N(p,
![]() ).
).
Замечание. Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Законом распределения такой СВ является биноминальный закон. Тогда при n биноминальный закон имеет два предельных распределения:
распределение Пуассона (при n и = np = const);
распределение Гаусса N(np,
 )
(при n
и p
= const).
)
(при n
и p
= const).
Пример. Вероятность “успеха” в одном испытании всего лишь p = 0,8. Сколько нужно провести испытаний, чтобы с вероятностью не менее 0,9 можно ожидать, что наблюдаемая частота “успеха” в испытаниях по схеме Бернулли отклонится от вероятности p не более чем на = 0,01?
Решение. Для сравнения решим задачу двумя способами:
а) На основе второго неравенства Чебышева имеем:
![]()
Следовательно:
![]()
б) Используя теорему
Муавра-Лапласа и учитывая, что если СВ
Y
N(,
),
то
![]() получаем:
получаем:
![]() Следовательно:
Следовательно:
![]()
![]()
 ,
т.е. почти в четыре раза меньше.
,
т.е. почти в четыре раза меньше.
При этом полученное значение настолько велико, что погрешностью используемой формулы можно пренебречь.
Задача 2. По полосе укреплений противника осуществляется залп из 100 орудий. При стрельбе из одного такого орудия математическое ожидание числа попаданий равно 2, а среднеквадратическое отклонение числа попаданий равно 1,5. Найти приближенно вероятность того, что в полосу укреплений противника попадет от 180 до 220 снарядов.
Задача 3. Противник атакует полосу укреплений, используя в наступлении 50 танков. Вероятность вывода из строя танка в этом бою равна 0,4. Если выведено из строя не менее 35% танков, то противник прекращает свое наступление. Требуется найти вероятность того, что противник откажется от наступления.
Следующие утверждения и теоремы составляют основу законов, объединенных общим названием закон больших чисел.
Первое неравенство Чебышева. Если СВ X 0 имеет конечное значение = M[X], то для любого 0 справедливо:
P{X } / или P{X < } > 1 - /.
Второе (основное) неравенство Чебышева. Если СВ X имеет конечные значения = M[X] и 2 = D[X], то для любого 0 справедливо:
P{X - } 2/2 или P{X - < } > 1 - 2/2.
Последовательность
СВ X1,
X2,
..., Xn,
... называется сходящийся
по вероятности при n
к СВ X
(обозначение:
![]() при n
),
если для любого, сколь угодно малого
> 0 справедливо
при n
),
если для любого, сколь угодно малого
> 0 справедливо
![]() ,
или, иными словами, для любых, сколь
угодно малых чисел
> 0 и
0 найдется номер k,
что для всех n
k
выполняется условие:
,
или, иными словами, для любых, сколь
угодно малых чисел
> 0 и
0 найдется номер k,
что для всех n
k
выполняется условие:
P{Xn - X < } > 1 - .
Теорема (Закон больших чисел в форме Чебышева). Если попарно независимые СВ X1, X2, ..., Xn, ... имеют конечные значения M[Xi] = i и D[Xi] = i2 2, то для любого 0 справедливо следующее:
![]() где
где
![]()
![]() или
или
![]() при n
.
при n
.
Следствие. Если в условии теоремы СВ X1, ..., Xn, ... имеют одинаковые значения M[Xi] = , то для любого 0 справедливо следующее:
![]() где
где
![]() или
или
![]() при n
.
при n
.
Теорема (Закон больших чисел в форме Бернулли). Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n частота “успехов” сходится по вероятности к p, где p - вероятность “успеха” в одном испытании, т.е.:
![]() при n
или
при n
или
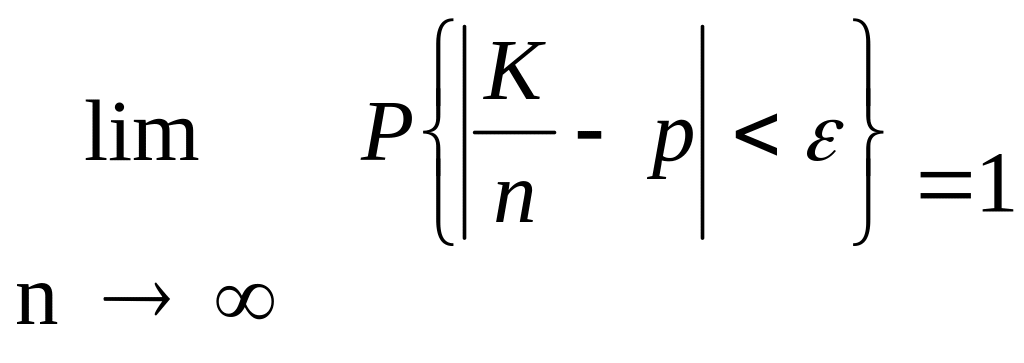 для любого
для любого
Лекция 9 Элементы математической статистики
(Раздел 6)
План лекции
Генеральная совокупность и выборка.
Сущность выборочного метода.
Дискретные и интервальные вариационные ряды.
Полигон и гистограмма.
Числовые характеристики выборки.
Понятие точечной оценки
Точечная оценка для генеральной средней, генеральной дисперсии, генерального среднеквадратического отклонения.
Понятие интервальной оценки.
Надежность доверительного интервала.
Интервальная оценка математического ожидания нормального распределения при известной дисперсии.
Интервальная оценка математического ожидания нормального распределения при неизвестной дисперсии.
Интервальная оценка математического ожидания нормального распределения при неизвестной дисперсии.
Точечная оценка вероятности события.
Интервальная оценка вероятности события.
Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.
В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей – свойства и взаимосвязи этих величин (распределений).
Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.
При этом возникают, например, следующие вопросы: Если мы наблюдаем одну случайную величину – как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?
Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин — что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?
Часто бывает возможно высказать некие предположения о распределении, спрятанном в “черном ящике”, или о его свойствах. В этом случае по опытным данным требуется подтвердить или опровергнуть эти предположения (“гипотезы”). При этом надо помнить, что ответ “да” или “нет” может быть дан лишь с определенной степенью достоверности, и чем дольше мы можем продолжать эксперимент, тем точнее могут быть выводы. Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента – например, о наличии функциональной зависимости между наблюдаемыми величинами, о нормальности распределения, о его симметричности, о наличии у распределения плотности или о его дискретном характере, и т.д.
Итак, о (математической) статистике имеет смысл вспоминать, если
имеется случайный эксперимент, свойства которого частично или полностью неизвестны,
мы умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое (а лучше – какое угодно) число раз.
Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.
Математической статистикой называется раздел прикладной математики, изучающий методы сбора, обработки и анализа экспериментальных данных.
Предметом исследования в математической статистике является совокупность объектов, однородных относительно некоторых признаков.
Например, мальчики 10 лет г. Уссурийска; пловцы-мастера спорта России.
Совокупность из всех объектов, объединенных этими признаками, называется генеральной. Задачей исследования является изучение признаков генеральной совокупности, которые определяются влиянием некоторых случайных факторов.
Например, изучение физической подготовленности мальчиков 10 лет г. Уссурийска.
Для решения задач исследования проводится эксперимент (измерение, тестирование, анкетирование), в результате которого получают значение некоторой случайной величины (результаты тестирования, количество баллов). Если в эксперименте участвуют все объекты генеральной совокупности, то такое обследование называют сплошным.
На практике обычно применяют выборочный метод, который заключается в том, что из генеральной совокупности случайным образом извлекают n элементов. Эти элементы называются выборочной совокупностью или выборкой. Количество элементов в выборке называется ее объемом. Исследователь изучает и анализирует выборочную совокупность и на основании полученных показателей делает вывод о параметрах генеральной совокупности.
Допустим, из генеральной совокупности извлечена выборка объемом n, измерена некоторая величина Х, в результате чего получен ряд значений х1, х2, . . . хn. Этот ряд называется простым статистическим рядом.
Полученная
в результате статистического наблюдения
выборка
из n
значений (вариант)
изучаемого количественного признака
X
образует вариационный
ряд.
Ранжированный
вариационный ряд получают, расположив
варианты xj ,
где
![]() ,
в порядке возрастания значений, то есть
,
в порядке возрастания значений, то есть
![]() .
.
Изучаемый признак X может быть дискретным, то есть его значения отличаются на конечную, заранее известную величину (год рождения, тарифный разряд, число людей), или непрерывным, то есть его значения отличаются на сколь угодно малую величину (время, вес, объем, стоимость).
Частотой mi в случае дискретного признака X называют число одинаковых вариант xi , содержащихся в выборке. В ранжированном вариационном ряду одинаковые варианты очевидно расположены подряд:
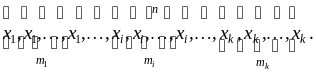
Вариационный
ряд для дискретного
признака X
принято наглядно и компактно представлять
в виде таблицы, в первой строке которой
указаны k
различных значений xi
изучаемого признака, а во второй строке
– соответствующие этим значениям
частоты mi ,
где
![]() .
Такую таблицу называют статистическим
(выборочным) распределением.
.
Такую таблицу называют статистическим
(выборочным) распределением.
Переход от исходного вариационного ряда дискретного признака X к соответствующему статистическому распределению поясним на простом примере:
вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем) – 7, 17, 14, 17, 10, 7, 7, 14, 7, 14;
ранжированный вариационный ряд –
xj :
![]() ,
где
,
где
![]() ,
n
= 10;
,
n
= 10;
соответствующее статистическое распределение (
 ,
k
= 4):
,
k
= 4):
xi |
7 |
10 |
14 |
17 |
mi |
4 |
1 |
3 |
2. |
Статистическое распределение для непрерывного признака X принято представлять интервальным рядом – таблицей, в первой строке которой указаны k интервалов значений изучаемого признака X вида (xi–1 – xi ), а во второй строке – соответствующие этим интервалам частоты mi , где . Обозначение (xi–1 – xi ) – указывает не разности, а все значения признака X от xi–1 до xi , кроме правой границы интервала xi .
Для непрерывного признака X частота mi – число различных xj , попавших в соответствующий интервал: xj[xi–1 ; xi ):
x3
xn
xn–1
xj+1
xj+2
xj
x4
x1
x2
xj :



X
xk
xk–1
xi
xi–1
x1
mk =
2
mi =
3
m1 =
4
x0
Переход от исходного вариационного ряда непрерывного признака X к соответствующему статистическому распределению поясним на простом примере:
вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем) –3,14; 1,41; 2,87; 3,62; 2,71; 3,95;
ранжированный вариационный ряд – xj : 1,41; 2,71; 2,87; 3,14; 3,62; 3,95; где , n = 6;
соответствующее статистическое распределение ( , k = 3):
xi |
1–2 |
2–3 |
3–4 |
mi |
1 |
2 |
3. |
Если число различных значений дискретного признака очень велико, то для удобства дальнейших вычислений и наглядности статистическое распределение такого дискретного признака также может быть представлено в виде интервального ряда.
Вместо
частот mi
во второй строке могут быть указаны
относительные
частоты
![]() (частости).
Очевидно, что сумма частот равна объему
выборки (выборочной совокупности) n
, а сумма относительных частот (частостей)
равна единице:
(частости).
Очевидно, что сумма частот равна объему
выборки (выборочной совокупности) n
, а сумма относительных частот (частостей)
равна единице:
![]()
![]() .
.
Далее показаны четыре возможных формы представления статистических распределений с соответствующими краткими названиями:
-
Дискретный ряд частот
Интервальный ряд частот
xi
x1
x2
…
xk
xi–1–xi
x0–x1
x1–x2
…
xk–1–xk
mi
m1
m2
mk ,
mi
m1
m2
…
mk ,
Дискретный ряд частостей
Интервальный ряд частостей
xi
x1
x2
…
xk
xi–1–xi
x0–x1
x1–x2
…
xk–1–xk
wi
w1
w2
wk ,
wi
w1
w2
…
wk .
Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд распределения называют кумулятивным.
Накопленной частотой называется число значений признака Х, меньших заданного значения x : H(x) = m(Х x), то есть, число вариант xj в выборке, отвечающих условию xj < x.
Переход от дискретного ряда частот к кумулятивному ряду – дискретному ряду накопленных частот задается соотношениями:
![]()
или в табличной форме:
xi |
x1 |
x2 |
x3 |
… |
xi |
… |
xk |
xk+1 |
H(xi) |
0 |
m1 |
m1+m2 |
… |
H(xi–1) + mi–1 |
… |
H(xk–1) + mk–1 |
H(xk) + mk= n. |
Переход от интервального ряда частот к кумулятивному ряду – интервальному ряду накопленных частот задается соотношениями:
![]()
или в табличной форме:
xi–1–xi |
––x0 |
x0–x1 |
x1–x2 |
… |
xi–1–xi |
… |
xk–1–xk |
H(xi) |
0 |
m1 |
m1+m2 |
… |
H(xi–1) + mi |
… |
H(xk–1) + mk= n. |
Накопленной
относительной частотой
(накопленной
частостью)
называется отношение числа значений
признака Х,
меньших заданного значения x
, к объему выборки n :
![]() , то есть, доля вариант xj
в выборке, отвечающих условию xj < x.
, то есть, доля вариант xj
в выборке, отвечающих условию xj < x.
По
аналогии с теоретической
функцией
распределения генеральной совокупности
![]() ,
которая определяет вероятность
события
Х
,
которая определяет вероятность
события
Х ![]() :
= P(Х
),
вводят понятие эмпирической
функции распределения
:
= P(Х
),
вводят понятие эмпирической
функции распределения
![]() ,
которая определяет относительную
частоту
этого же события
Х
,
то есть
=
,
которая определяет относительную
частоту
этого же события
Х
,
то есть
=
![]() .
Таким образом, эмпирическая
функция распределения
задается рядом накопленных
относительных частот.
.
Таким образом, эмпирическая
функция распределения
задается рядом накопленных
относительных частот.
Из теоремы Бернулли следует, что стремится по вероятности к F(x):
![]()
поэтому эмпирическую функцию распределения можно использовать для оценки теоретической функции распределения генеральной совокупности.
Дискретный ряд накопленных относительных частот может быть получен двумя равноправными способами:
1) переход от дискретного ряда частостей к кумулятивному ряду – дискретному ряду накопленных частостей задается соотношениями:
![]()
или в табличной форме:
xi |
x1 |
x2 |
x3 |
… |
xi |
… |
xk |
xk+1 |
|
0 |
w1 |
w1+w2 |
… |
(xi–1) + wi–1 |
… |
(xk–1) + wk–1 |
(xk) + wk= 1; |
2) переход от дискретного ряда накопленных частот к дискретному ряду накопленных частостей задается соотношением:
![]()
Интервальный ряд накопленных относительных частот может быть получен двумя равноправными способами:
1) переход от интервального ряда частостей к кумулятивному ряду – интервальному ряду накопленных частостей задается соотношениями:
![]()
или в табличной форме:
xi–1–xi |
––x0 |
x0–x1 |
x1–x2 |
… |
xi–1–xi |
… |
xk–1–xk |
(xi) |
0 |
w1 |
w1+w2 |
… |
(xi–1) + wi |
… |
(xk–1) + wk= 1; |
2) переход от интервального ряда накопленных частот к интервальному ряду накопленных частостей задается соотношением:
![]()
Для наглядности принято использовать следующие формы графического представления статистических распределений:
дискретный ряд изображают в виде полигона. Полигон частот – ломаная линия, отрезки которой соединяют точки с координатами ( i ,
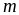 i);
аналогично, полигон
относительных частот
– ломаная, отрезки которой соединяют
точки с координатами (
i);
аналогично, полигон
относительных частот
– ломаная, отрезки которой соединяют
точки с координатами (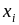 ,
wi );
,
wi );
интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых – интервалы длиной
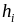 ,
а высоты – плотности частот
,
а высоты – плотности частот
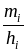 .
В случае гистограммы
относительных частот
высоты прямоугольников – плотности
относительных частот
.
В случае гистограммы
относительных частот
высоты прямоугольников – плотности
относительных частот
 .
Здесь в общем случае
.
Здесь в общем случае
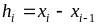 ,
однако на практике чаще всего полагают
величину h
одинаковой для всех интервалов:
,
однако на практике чаще всего полагают
величину h
одинаковой для всех интервалов:
 .
Очевидно для ранжированного вариационного
ряда
.
Очевидно для ранжированного вариационного
ряда
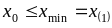 ;
;
 .
В скобках указаны индексы j
исходного
ранжированного вариационного ряда.
.
В скобках указаны индексы j
исходного
ранжированного вариационного ряда.
Площадь гистограммы есть сумма площадей ее прямоугольников:
![]()
![]()
таким
образом, площадь гистограммы частот
![]() равна объему выборки, а площадь гистограммы
относительных частот
равна объему выборки, а площадь гистограммы
относительных частот
![]() равна единице.
равна единице.
В
теории вероятностей гистограмме
относительных частот соответствует
график плотности распределения
вероятностей
![]() .
Поэтому гистограмму можно использовать
для подбора закона распределения
генеральной совокупности;
.
Поэтому гистограмму можно использовать
для подбора закона распределения
генеральной совокупности;
кумулятивные ряды графически изображают в виде кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат – накопленные частоты Н( ) или относительные накопленные частоты , а затем точки с координатами ( i ; H( i )) или ( i ;
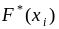 )
соединяют отрезками прямой. В теории
вероятностей кумуляте соответствует
график интегральной функции распределения
.
)
соединяют отрезками прямой. В теории
вероятностей кумуляте соответствует
график интегральной функции распределения
.
Замечание 1. Если в статистическом исследовании исходным является статистическое распределение в виде интервального ряда (сгруппированные данные), а исходный вариационный ряд недоступен, то точное расположение отдельных вариант, попавших в каждый из интервалов неизвестно. Только выбирая в качестве аргумента эмпирической функции распределения правую границу интервала (xi–1–xi), мы уверены, что все варианты, попавшие в этот интервал, будут учтены (просуммированы) в значении накопленной частоты (накопленной относительной частоты), соответствующей этому интервалу.
Поэтому в случае интервального ряда значения и H(x) точно определены лишь для правой границы интервала: x = xi . В остальных точках интервала xi–1 < x xi значения и H(x) можно задать лишь приближенно. Примером может служить кумулята, отрезки прямых которой представляют собой выраженную в графической форме линейную интерполяцию значений и H(x) на интервале xi–1 < x xi .
Замечание
2. В случае
дискретного ряда использовать кумуляту
для изображения
и H(x)
можно лишь условно, для наглядности.
Более корректным является изображение
эмпирической функции распределения
(а также H(x))
по аналогии с теоретической функцией
распределения
![]() дискретной случайной величины (см. рис.
2) ступенчатым графиком – отрезками
прямых, параллельных оси абсцисс; длины
отрезков – hi
= xi
– xi–1
, расстояния
от отрезков до оси абсцисс –
дискретной случайной величины (см. рис.
2) ступенчатым графиком – отрезками
прямых, параллельных оси абсцисс; длины
отрезков – hi
= xi
– xi–1
, расстояния
от отрезков до оси абсцисс –
![]() (или H(xi)).
(или H(xi)).
Пример 1. Имеется распределение 80 предприятий по числу работающих на них (чел.):
|
150 |
250 |
350 |
450 |
550 |
650 |
750 |
|
1 |
3 |
7 |
30 |
19 |
15 |
5 . |
Решение. Признак Х – число работающих (чел.) на предприятии. В данной задаче признак Х является дискретным. Поскольку различных значений признака сравнительно немного – k = 7, применять интервальный ряд для представления статистического распределения нецелесообразно (в прикладной статистике в подобных задачах часто используют именно интервальный ряд). Ряд распределения – дискретный. Построим полигон распределения частот

Пример 2. Дано распределение 100 рабочих по затратам времени на обработку одной детали (мин):
xi–1–xi |
22–24 |
24–26 |
26–28 |
28–30 |
30–32 |
32–34 |
|
2 |
12 |
34 |
40 |
10 |
2 . |
Решение.
Признак Х –
затраты времени на обработку одной
детали (мин). Признак Х
– непрерывный,
ряд распределения – интервальный.
Построим гистограмму частот, предварительно
определив
![]() (k = 6)
и плотность частоты
(k = 6)
и плотность частоты
![]() :
:
xi–1–xi |
22–24 |
24–26 |
26–28 |
28–30 |
30–32 |
32–34 |
|
1 |
6 |
17 |
20 |
5 |
1 . |
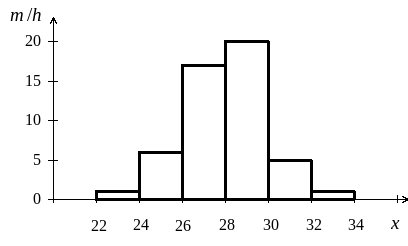
Пример 3. В распределении, данном в примере 1, найти накопленные частоты H( i ) и построить кумуляту.
Решение. Используем: H(x1) = 0, H(xi) = H(xi–1) + mi–1 (i=2,3,, k+1 , k = 7).
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
xi |
150 |
250 |
350 |
450 |
550 |
650 |
750 |
850 |
mi |
1 |
3 |
7 |
30 |
19 |
15 |
5 |
0 |
H( i ) |
0 |
0+1=1 |
1+3=4 |
4+7=11 |
11+30=41 |
41+19=60 |
60+15=75 |
75+5=80. |
На рис. 3 показана кумулята распределения предприятий по числу работающих (чел.).
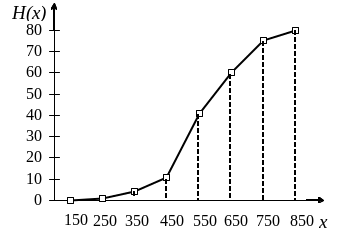
Пример 4. В распределении, данном в примере 2, составить эмпирическую функцию распределения и построить кумуляту относительных частот.
Решение.
Используем: H(x0)
= 0, H(xi)
= H(xi–1)
+ mi
(i=1,2,,
k
,
k = 6).
![]() ;
;
![]() Проверка:
Проверка:
![]() 1.
1.
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
xi–1–xi |
––22 |
22–24 |
24–26 |
26–28 |
28–30 |
30–32 |
32–34 |
mi |
0 |
2 |
12 |
34 |
40 |
10 |
2 |
H( i ) |
0 |
0+2=2 |
2+12=14 |
14+34=48 |
48+40=88 |
88+10=98 |
98+2=100 |
|
0 |
0,02 |
0,14 |
0,48 |
0,88 |
0,98 |
1. |
Построим кумуляту распределения
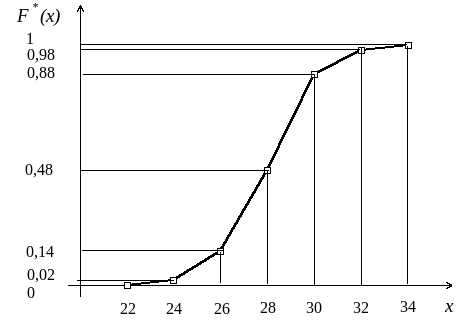
Для описания основных свойств статистических распределений чаще всего используют выборочные характеристики следующих двух видов:
средние;
Выборочная средняя: |
а) характеризует типичное для выборки значение признака X; б) приближенно характеризует (оценивает) типичное для генеральной совокупности значение признака X (см. п. 3.2); |
||
|
– средняя арифметическая; применяется к вариационному ряду (данные наблюдения не сгруппированы); |
||
|
– взвешенная средняя арифметическая (частоты mi , и частости wi называют весами); используется, если данные сгруппированы; непосредственно применима только к статистическому распределению дискретного признака (дискретному ряду). |
||
|
|||
Структурные (порядковые) средние. |
Если
|
||
хме = хj+1 , если n = 2j+1 – нечетное. |
Медиана
– это серединное значение признака
X;
по определению:
|
||
хмo = xi , если mi = mmax (справедливо только для дискретного ряда). |
Мода – наиболее часто встречающееся значение признака X. |
||
2) характеристики вариации (рассеяния).
|
– выборочная
дисперсия есть
выборочная средняя арифметическая
квадратов отклонений значений признака
X
от выборочной средней
|
|||
|
– выборочная дисперсия; применяется к вариационному ряду (данные наблюдения не сгруппированы); |
|||
|
– выборочная взвешенная дисперсия; используется, если данные сгруппированы; непосредственно применима только к статистическому распределению дискретного признака (дискретному ряду); |
|||
|
– средний квадрат есть выборочная средняя арифметическая квадратов значений признака X (для вариационного ряда и для дискретного распределения соответственно). |
|||
|
– выборочное среднее квадратическое отклонение есть арифметическое значение корня квадратного из дисперсии; оно показывает, на сколько в среднем отклоняются значения xj признака X от выборочной средней . |
|||
|
||||
R = хmax – хmin |
– размах вариации. |
|||
|
– коэффициент вариации; применяют для сравнения вариации признаков сильно отличающихся по величине, или имеющих разные единицы измерения (разные наименования). |
|||
Замечание.
Если исходный вариационный ряд недоступен,
приведенные выше формулы вычисления
выборочных характеристик, применимые
только к дискретному ряду, могут быть
использованы для приближенного
вычисления выборочных характеристик
непрерывного признака, представленного
интервальным рядом. Для этого предварительно
каждый интервал xi–1–xi
заменяется его серединой
![]() = (xi–1+ xi) / 2,
то есть производится замена интервального
ряда дискретным, соответствующим ему
приближенно.
= (xi–1+ xi) / 2,
то есть производится замена интервального
ряда дискретным, соответствующим ему
приближенно.
Пример 5. Найти числовые характеристики распределения предприятий по числу работающих (пример 1).
Решение. Признак Х – число работающих (чел.) на предприятии. Для расчета характеристик данного распределения удобнее использовать таблицу:
Число работающих на предприятии, (хi ,чел.) |
Число предприятий (mi) |
хi mi |
Н(хi) |
(хi
– |
хi2 mi |
150 250 350 450 550 650 750 |
1 3 7 30 19 15 5 |
150 750 2450 13500 10450 9750 3750 |
0 1 4 11 41 60 75 |
129600 202800 179200 108000 30400 294000 288000 |
22500 187500 857500 6045000 5747500 6337500 2812500 |
Итого |
80 |
40800 |
- |
1232000 |
22040000 . |
![]() 510
(чел.) – среднее число работающих на
предприятии.
510
(чел.) – среднее число работающих на
предприятии.
Легко убедиться, что в случае дискретного признака Х в ранжированном вариационном ряду xj = xi при Н(хi) + 1 j Н(хi+1). Для рассматриваемого примера: xj = 450 при 12 j 41.
Объем выборки n = 80 – число четное. Пусть n = 2j , тогда j = 40. Поэтому:
![]() 450
(чел.).
450
(чел.).
Частота достигает максимума: mi = mmax = 30 при xi = 450, поэтому:
хмо = 450 (чел.).
Очевидно хмo хме – распределение асимметричное (см. рис. 1).
R = хmax – хmin = 750 – 150 = 600 (чел.).
Дисперсию рассчитываем двумя способами.
1)
![]()
2)
![]()
![]() =
275500 – (510)2
= 15400.
=
275500 – (510)2
= 15400.
![]() (численность
работающих на каждом предприятии
отклоняется от средней численности в
среднем на 124 чел.)
(численность
работающих на каждом предприятии
отклоняется от средней численности в
среднем на 124 чел.)
![]()
24,3 %.
24,3 %.
На практике считают,
что если
![]() 33 %
, то совокупность однородная. В данном
случае исследуемая совокупность
однородная.
33 %
, то совокупность однородная. В данном
случае исследуемая совокупность
однородная.
Пример 6. Найти числовые характеристики распределения затрат времени на обработку одной детали (пример 2).
Решение. Признак Х – затраты времени на обработку одной детали (мин) – непрерывный. Распределение задано интервальным рядом. Характеристики такого ряда находят по тем же формулам, что и для дискретного ряда, предварительно заменив интервальный ряд дискретным. Для этого каждый интервал xi–1–xi заменяется его серединой . Расчеты представим в таблице:
Затраты времени на обработку 1 детали (Х, мин): xi–1–xi |
Число рабочих (mi) |
|
mi |
Н( ) |
|
( )2 mi |
22–24 24–26 26–28 28–30 30–32 32–34 |
2 12 34 40 10 2 |
23 25 27 29 31 33 |
46 300 918 1160 310 66 |
0 2 14 48 88 98 |
50 108 34 40 90 50 |
1058 7500 24786 33640 9610 2178 |
Итого |
100 |
- |
2800 |
- |
372 |
78772 . |
![]() 28 (мин) – среднее
время на обработку одной детали.
28 (мин) – среднее
время на обработку одной детали.
Легко убедиться,
что в случае дискретного признака Х
в ранжированном вариационном ряду xj =
при Н(
) + 1 j Н(![]() ).
Для рассматриваемого примера:
xj
= 29 при
49 j 88.
).
Для рассматриваемого примера:
xj
= 29 при
49 j 88.
Объем выборки n = 100 – число четное. Пусть n = 2j , тогда j = 50. Поэтому:
![]() 29
(мин).
29
(мин).
Частота достигает максимума: mi = mmax = 40 при xi = 29, поэтому:
хмо = 29 (мин).
Очевидно хмo хме – распределение асимметричное (см. рис. 2).
R = хmax – хmin = 34 – 22 = 12 (мин).
Дисперсию рассчитываем двумя способами.
1)
![]() ;
;
2)
![]() ;
;
= 787,72 – (28)2 = 3,72.
![]() 1,93
(мин), то есть затраты времени на обработку
одной детали каждым рабочим отклоняются
от средних затрат времени в среднем на
1,93 мин.
1,93
(мин), то есть затраты времени на обработку
одной детали каждым рабочим отклоняются
от средних затрат времени в среднем на
1,93 мин.
![]() – совокупность
однородная.
– совокупность
однородная.