
- •230115 «Программирование в компьютерных системах»
- •1. Правило произведения
- •2. Правило суммы
- •3. Комбинаторный метод вычисления вероятностей
- •Равномерный закон распределения
- •Показательный закон распределения
- •Нормальный (гауссовский) закон распределения
- •Точечные оценки параметров
- •Точечные оценки m[X], d[X] и их свойства
- •Методы получения Точечных оценок
- •Интервальные оценки (доверительные интервалы)
- •Общие понятия теории графов
- •Сети, потоки в сетях. Теорема Форда – Фалкерсона
- •Процесс гибели – размножения и циклический процесс.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
высшего профессионального образования
«Московский государственный университет экономики, статистики
и информатики (МЭСИ)»
Лекционный материал по предмету
Теория вероятностей и математическая статистика
(Математический и общий естественнонаучный цикл)
основной профессиональной образовательной программы СПО
230115 «Программирование в компьютерных системах»
Разработала преподаватель Брянского филиала МЭСИ Орлова С.И.
Брянск 2013
Лекция 1 Элементы комбинаторики
План лекции
Правило умножения и правило сложения.
Упорядоченные выборки, размещения с повторениями и без повторений. Перестановки.
Неупорядоченные выборки, сочетания с повторениями и без повторений.
В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.
1. Правило произведения
Если первое событие может произойти n1 способами, а второе - n2 способами независимо от первого, то совместная реализация может произойти n1n2 способами.
2. Правило суммы
Если первое событие может произойти n1 способами, а второе - n2 способами независимо от первого, то первое или второе события могут произойти n1+n2 способами.
3. Комбинаторный метод вычисления вероятностей
При подсчете числа элементарных исходов, составляющих события в классической схеме, часто используются известные формулы комбинаторики. Каждая из комбинаторных формул определяет общее число элементарных исходов в некотором идеализированном эксперименте по выбору наудачу m элементов из n различных элементов исходного множества E = {e1, e2, ..., en}.
При постановке каждого такого эксперимента строго оговорено, каким способом производится выбор и что понимается под различными выборками. Существуют две принципиально отличные схемы выбора: в первой схеме выбор осуществляется без возвращения элементов (это значит, что отбираются либо сразу все m элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества). Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательным перемешиванием исходного множества перед следующим выбором. После того, как выбор тем или иным способом осуществлен, отобранные элементы (или их номера) могут быть либо упорядочены (т.е. выложены в последовательную цепочку), либо нет. В результате получаются следующие четыре различные постановки эксперимента по выбору наудачу m элементов из общего числа n различных элементов множества Е.
Схема выбора, приводящая к сочетаниям
Если опыт состоит в выборе m элементов без возвращения и без упорядочивания, то различными исходами следует считать m-элементные подмножества множества E, имеющие различный состав. Получаемые при этом комбинации элементов (элементарные исходы) носят название сочетания из n элементов по m, а их общее число N() определяется по формуле: Cmn = n!/[m!(n - m)!] = n(n - 1)...(n - m + 1)/m!.
Для чисел Cmn, называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:
Cmn = Cn-mn (свойство симметрии),
Ckn+1 = Ckn + Ck-1n; C0n = 1 (рекуррентное соотношение),
C0n + C1n + ... + Cnn = 2n (следствие биномиальной формулы Ньютона).
Пример 1. Множество Е содержит 10 первых букв русского алфавита. Сколько различных алфавитов из трех букв можно составить из данного множества букв? Какова вероятность того, что случайно выбранный алфавит будет содержать букву «a»?
Решение Число различных алфавитов равно числу трехэлементных подмножеств множества Е (числу сочетаний из 10 элементов по 3): N() = C310 = 1098/(123) = 120.
Пусть событие A - случайно выбранный алфавит из трех букв, содержащий букву «a». Число элементов множества А равно числу всех возможных способов отобрать две буквы из девяти (из десяти букв исключена буква «a»), т.е. равно числу сочетаний из 9 элементов по 2: N(A) = C29 = 98/2 = 36.
Таким образом, Р(A) = N(A)/N() = 36/120 = 0,3.
Схема выбора, приводящая к размещениям
Если опыт состоит в выборе m элементов без возвращения, но с упорядочиванием их по мере выбора в последовательную цепочку, то различными исходами данного опыта будут упорядоченные m-элементные подмножества множества Е, отличающиеся либо набором элементов, либо порядком их следования. Получаемые при этом комбинации элементов (элементарные исходы) называются размещениями из n элементов по m, а их общее число N() определяется формулой:
Amn = Cmnm! = n!/(n - m)! = n(n - 1)...(n - m + 1).
Если n = m, то опыт фактически состоит в произвольном упорядочивании множества Е, т.е. сводится к случайной перестановке элементов всего множества. Тогда N() = Ann = n!.
Пример 2. Группа, состоящая из 8 человек, занимает места за круглым столом в случайном порядке. Какова вероятность того, что при этом два определенных лица окажутся сидящими рядом?
Решение. Так как упорядочивается все множество из 8 элементов, то N() = A88 = 40320. Событию А благоприятствуют такие размещения, когда два отмеченных лица сидят рядом: всего 8 различных соседних пар мест за круглым столом, на каждой из которых отмеченные лица могут сесть двумя способами, при этом остальные 6 человек размещаются на оставшиеся места произвольно, поэтому по формуле о числе элементов прямого произведения множеств получаем N(A) = 286!. Следовательно Р(A) = N(A)/N() = 2/7.
Схема выбора, приводящая к сочетаниям с повторениями
Если опыт состоит в выборе с возвращением m элементов множества E = {e1, e2, ..., en}, но без последующего упорядочивания, то различными исходами такого опыта будут всевозможные m-элементные наборы, отличающиеся составом. При этом отдельные наборы могут содержать повторяющиеся элементы. Например, при m = 4 наборы {e1, e1, e2, e1} и {e2, e1, e1, e1} неразличимы для данного эксперимента, а набор {e1, e1, e3, e1} отличен от любого из предыдущих. Получающиеся в результате данного опыта комбинации называются сочетаниями с повторениями, а их общее число определяется формулой N() = Cmn+m-1.
Пример 3. В библиотеке имеются книги по 16 разделам науки. Поступили очередные четыре заказа на литературу. Считая, что любой состав заказанной литературы равновозможен, найти вероятности следующих событий: А - заказаны книги из различных разделов наук, В - заказаны книги из одного и того же раздела науки.
Решение. Число всех равновероятных исходов данного эксперимента равно, очевидно, числу сочетаний с повторениями из 16 элементов по 4, т.е. N()= C416+4-1 = C419.
Число исходов, благоприятствующих событию A, равно числу способов отобрать без возвращения четыре элемента из 16, поэтому Р(A) = N(A)/N() = C416/C419 0,47.
Число исходов, благоприятствующих событию В, равно числу способов выбрать один элемент из 16, поэтому Р(A) = N(A)/N() = C116/C419 0,004.
Схема выбора, приводящая к размещениям с повторениями
Если выбор m элементов из множества E = {e1, e2, ..., en}, производится с возвращением и с упорядочиванием их в последовательную цепочку, то различными исходами будут всевозможные m-элементные наборы (вообще говоря, с повторениями), отличающиеся либо составом элементов, либо порядком их следования. Например, при m = 4 наборы {e1, e1, e2, e1}, {e2, e1, e1, e1} и {e1, e1, e3, e1} являются различными исходами данного опыта. Получаемые в результате различные комбинации называются размещениями, с повторениями, а их общее число определяется формулой
N()= nm.
Пример 4. Опыт состоит в четырехкратном выборе с возвращением одной из букв алфавита E = {а, б, к, о, м} и выкладывании слова в порядке поступления букв. Какова вероятность того, что в результате будет выложено слово «мама»?
Решение. Число элементов множества, равновероятных исходов равно числу размещений с повторениями из 5 элементов по 4 т.е. N()= 54. Слову «мама» соответствует лишь один возможный исход. Поэтому Р(A) = N(A)/N() = 1/54 0,0016.
Схема упорядоченных разбиений
Пусть множество E состоит из m различных элементов. Рассмотрим опыт, состоящий в разбиении множества E случайным образом на s подмножеств E1, E2, ..., Es таким образом, что:
1. Множество Еi содержит ровно ni элементов, где i = 1, 2, ..., s.
2. Множества Еi упорядочены по количеству элементов ni.
3. Множества Еi, содержащие одинаковое количество элементов, упорядочиваются произвольным образом. Например, при n = 7, n1 = 2, n2 = 2, n3 = 3 разбиения {E1 = {e1, е2}, Е2 = {e3, е4}, Е3 = {e5, е6, e7}} и {E1 ={e3, е4}, Е2 ={e1, е2}, Е3 = {e5, е6, e7}} являются различными исходами данного опыта.
Число всех элементарных исходов в данном опыте определяется формулой N() = n!/(n1! n2! ... ns!).
Пример 5. Десять приезжих мужчин, среди которых Петров и Иванов, размещаются в гостинице в два трехместных и один четырехместный номер. Сколько существует способов их размещения? Какова вероятность того, что Петров и Иванов попадут в четырехместный номер?
Решение. Разбиения в данном опыте характеризуются следующими параметрами: s = 3, n = 10, n1 = 3, n2 = 3, n3 = 4. Тогда N() = 10!/(3!3!4!) = 4200.
Пусть событие А - Петров и Иванов попадут в одни четырехместный номер. Благоприятствующие событию А исходы соответствуют разбиениям со следующими параметрами: s = 3, n = 8, n1 = 3, n2 = 3, n3 = 2. Тогда N(A) = 8!/(3!3!2!) = 560. Искомая вероятность Р(A) = N(A)/N() = 560/4200 = 2/15.
Лекция 2 Случайные события. Классическое определение вероятности
(Тема 2.1.)
План лекции
Понятие случайного события.
Совместные и несовместные события.
Полная группа событий.
Равновозможные события.
Арифметические действия над событиями.
Понятие вероятности.
Классическое определение вероятности.
Противоположное событие.
Условная вероятность.
Теорема умножения событий.
Независимые события.
Вероятность суммы совместных и несовместных событий.
Случайные события. Частота. Вероятность. Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий). Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:
а) достоверное событие – событие, которое всегда происходит при проведении опыта;
б) невозможное событие – событие, которое в результате опыта произойти не может;
в) случайное событие – событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным – выпадение 10 очков, а случайным – выпадение 3 очков. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом). Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие. События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... . Определение Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.
Пример 1. Два стрелка делают по одному выстрелу по мишени. Если событие А – попадание первого стрелка, а событие В – второго, то сумма А+В – это хотя бы одно попадание при двух выстрелах.
Пример 2. Если при броске игральной кости событием Аi назвать выпадение i очков, то выпадение нечетного числа очков является суммой событий А1+А2+А3.
Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В





 А В
А + В
А В
А + В


Определение Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.
Пример 3. В примере 1 ( два выстрела по мишени) событием АВ будет попадание обоих стрелков.
Пример 4. Если событие А состоит в том, что из колоды карт извлечена карта пиковой масти, а событие В – в том, что из колоды вынута дама, то событием АВ будет извлечение из колоды дамы пик.
Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А и В, является пересечение областей, соответствующих исходам, благоприятным А и В.

А В АВ
Определение Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет.
Пример 5. Вернемся к примеру 1, где А\ В – попадание первого стрелка при промахе второго.
Пример 6. В примере 4 А\В – извлечение из колоды любой карты пиковой масти, кроме дамы. Наоборот, В \А – извлечение дамы любой масти, кроме пик.



А В А - В
Введем еще несколько категорий событий.
Определение События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.
Замечание 1. Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек.
Замечание 2. Из определения несовместных событий следует, что их произведение является невозможным событием.
Определение Говорят, что события А1, А2,…,Ап образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы.
Замечание. В частности, если события, образующие полную группу, попарно несовместны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями.
Пример. События А1 – А6 (выпадение одного, двух,…, шести очков при одном броске игральной кости) образуют полную группу несовместных событий.
Определение События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.
При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Например, при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей.
Отметим, что само понятие вероятности, как и понятие случайного события, является аксиоматическим и поэтому не поддается строгому определению. То, что в дальнейшем будет называться различными определениями вероятности, представляет собой способы вычисления этой величины.
Определение Если все события, которые могут произойти в результате данного опыта,
а) попарно несовместны;
б) равновозможны;
в) образуют полную группу,
то говорят, что имеет место схема случаев.
Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п ( число возможных исходов), а при т из них происходит некоторое событие А (число благоприятных исходов).
Определение Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:
![]()
Примеры: выпадение любого числа очков при броске игральной кости, появление любой карты при случайном извлечении из колоды, выпадение герба или цифры при броске монеты и т.п.
Пусть при n испытаниях событие A появилось m раз. Отношение m/n называется частотой (относительной частотой) события A и обозначается Р(А)=m/n Опыт показывает, что при многократном повторении испытаний частота Р(А) случайного события обладает устойчивостью. Поясним это на примере. Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5. Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти. Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие. Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю. Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A. Теорема сложения вероятностей.
Вероятность р(А + В) суммы событий А и В равна
Р (А + В ) = р (А) + р (В) – р (АВ). Доказательство.
![]() что
и требовалось доказать.
что
и требовалось доказать.
Следствие 1. Теорему сложения можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С
Р(А + В + С) = р(А) + р(В) + р(С) – р(АВ) – р(АС) – р(ВС) + р(АВС) и т.д.
Следствие 2. Если события А и В несовместны, то тАВ = 0, и, следовательно, вероятность суммы несовместных событий равна сумме их вероятностей:
Р(А + В) = р(А) + р(В).
Определение
Противоположными
событиями
называют два несовместных события,
образующих полную группу. Если одно из
них назвать А, то второе принято обозначать
![]() .
Замечание. Таким образом,
заключается в том, что событие А не
произошло.
.
Замечание. Таким образом,
заключается в том, что событие А не
произошло.
Теорема Сумма вероятностей противоположных событий равна 1:
р(А) + р( ) = 1
Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5).
Пример Из урны, содержащей 2 белых и 6 черных шаров, случайным образом извлека-ются 5 шаров. Найти вероятность того, что вынуты шары разных цветов.
Решение. Событие , противоположное заданному, заключается в том, что из урны вынуто 5 шаров одного цвета, а так как белых шаров в ней всего два, то этот цвет может быть только черным. Множество возможных исходов опыта найдем по формуле (1.5):
![]()
а множество исходов, благоприятных событию - это число возможных наборов по 5 шаров только из шести черных:
![]()
Тогда
![]() а
а
![]()
Теорема умножения вероятностей.
Определение Назовем условной вероятностью р(В/А) события В вероятность события В при условии, что событие А произошло.
р (АВ) = р (А) · р (В/А).
Замечание. Понятие условной вероятности используется в основном в случаях, когда осуществление события А изменяет вероятность события В.
Примеры:
пусть событие А – извлечение из колоды в 32 карты туза, а событие В – то, что и вторая вынутая из колоды карта окажется тузом. Тогда, если после первого раза карта была возвращена в колоду, то вероятность вынуть вторично туз не меняется:
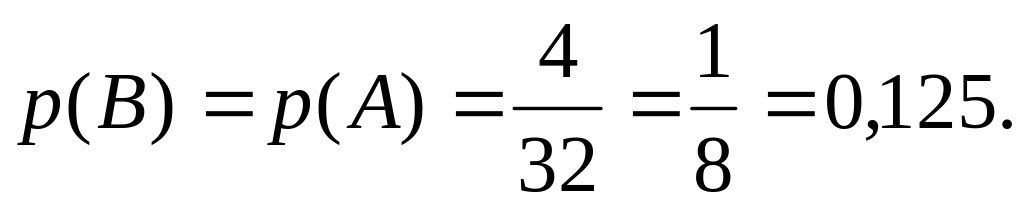 Если же первая карта в колоду не
возвращается, то осуществление события
А приводит к тому, что в колоде осталась
31 карта, из которых только 3 туза. Поэтому
Если же первая карта в колоду не
возвращается, то осуществление события
А приводит к тому, что в колоде осталась
31 карта, из которых только 3 туза. Поэтому
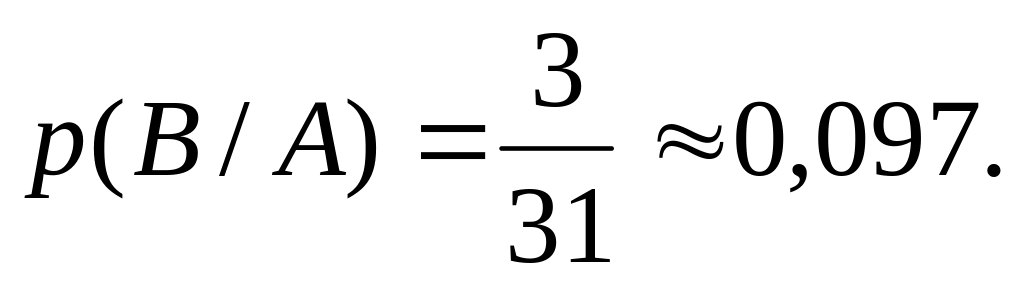
если событие А – попадание в самолет противника при первом выстреле из орудия, а В – при втором, то первое попадание уменьшает маневренность самолета, поэтому р(В/А) увеличится по сравнению с р(А).
Пример. Для поражения цели необходимо попасть в нее дважды. Вероятность первого попадания равна 0,2, затем она не меняется при промахах, но после первого попадания увеличивается вдвое. Найти вероятность того, что цель будет поражена первыми двумя выстрелами.
Решение. Пусть событие А – попадание при первом выстреле, а событие В – попадание при втором. Тогда р (А) = 0,2, р (В/А) = 0,4, р (АВ) = 0,2·0,4 = 0,08.
Следствие. Если подобным образом вычислить вероятность события ВА, совпадающего с событием АВ, то получим, что р (ВА) = р (В) · р (А/В). Следовательно, р (А) · р (В/А) = р (В) · р (А/В).
Определение Событие В называется независимым от события А, если появление события А не изменяет вероятности В, то есть р (В/А) = р (В).
Замечание. Если событие В не зависит от А, то и А не зависит от В. Действительно, из (2.7) следует при этом, что р (А) · р (В) = р (В) · р (А/В), откуда р (А/В) = р (А). Значит, свойство независимости событий взаимно.
Теорема умножения для независимых событий имеет вид:
р (АВ) = р (А) · р (В) , то есть вероятность произведения независимых событий равна произведению их вероятностей.
При решении задач теоремы сложения и умножения обычно применяются вместе.
Пример. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0,6 и 0,7. Найти вероятности следующих событий:
А – хотя бы одно попадание при двух выстрелах;
В – ровно одно попадание при двух выстрелах;
С – два попадания;
D – ни одного попадания.
Решение. Пусть событие Н1 – попадание первого стрелка, Н2 – попадание второго. Тогда
А
= Н1
+ Н2,
В =Н1![]()
![]() События Н1
и Н2
совместны и независимы, поэтому теорема
сложения применяется в общем виде, а
теорема умножения – в виде (2.8).
Следовательно, р(С) = 0,6·0,7 = 0,42, р(А)
= 0,6 + 0,7 – 0,42 = 0,88,
События Н1
и Н2
совместны и независимы, поэтому теорема
сложения применяется в общем виде, а
теорема умножения – в виде (2.8).
Следовательно, р(С) = 0,6·0,7 = 0,42, р(А)
= 0,6 + 0,7 – 0,42 = 0,88,
р(B)
= 0,6·0,3 + 0,7·0,4 = 0,46 (так как события
![]() и
и
![]() несовместны),
несовместны),
р(D) = 0,4·0,3 = 0,12. Заметим, что события А и D являются противоположными, поэтому
р(А) = 1 – р(D).
Вероятность появления хотя бы одного события.
Теорема
Вероятность
появления хотя бы одного из попарно
независимых событий А1,
А2,…,
Ап
равна р (А) = 1 – q1q2…qn
, где qi
– вероятность события
![]() ,
противоположного событию Аi
.
,
противоположного событию Аi
.
Пример. Сколько нужно произвести бросков монеты, чтобы с вероятностью не менее 0,9 выпал хотя бы один герб?
Решение. Вероятность выпадения герба при одном броске равна вероятности противопо-ложного события (выпадения цифры) и равна 0,5. Тогда вероятность выпадения хотя бы одного герба при п выстрелах равна 1- (0,5)п . Тогда из решения неравенства 1- (0,5)п > 0,9
следует, что п > log210 ≥ 4.
Аксиомы вероятностей. Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P(A)=m1/n, P(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,
Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P(A), P(B) и P(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B) Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом. Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию Р(А)=m/n . Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей: P(A+B)=P(A)+P(B)
Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то
Событием,
противоположным
событию A,
называется событие
![]() ,
состоящее в ненаступлении события A.
Очевидно, события A
и
несовместны.
Пусть, например, событие
A состоит
в том, что изделие удовлетворяет
стандарту; тогда противоположное событие
заключается в том, что изделие стандарту
не удовлетворяет. Пусть событие A
— выпадение
четного числа очков при однократном
бросании игральной кости; тогда
— выпадение
нечетного числа очков.
,
состоящее в ненаступлении события A.
Очевидно, события A
и
несовместны.
Пусть, например, событие
A состоит
в том, что изделие удовлетворяет
стандарту; тогда противоположное событие
заключается в том, что изделие стандарту
не удовлетворяет. Пусть событие A
— выпадение
четного числа очков при однократном
бросании игральной кости; тогда
— выпадение
нечетного числа очков.
Теорема 1. Для любого события A вероятность противоположного события Р( ) = 1- Р(А) выражается равенством
Теорема 2. Вероятность невозможного события равна нулю. Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.
Классическое определение вероятности. Как было сказано выше, при большом числе n испытаний частота P(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A. Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности). Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое. Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события. Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно). События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них. Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.
Очевидно, любое событие A и противоположное ему событие образуют полную группу. Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A. Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A. Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению. Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности. Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
|
1-я монета |
2-я монета |
1-й исход |
герб |
герб |
2-й исход |
герб |
надпись |
3-й исход |
надпись |
герб |
4-й исход |
надпись |
надпись |
Таким образом, P(герб,герб)=1/4. Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
|
1-я монета |
2-я монета |
1-й исход |
герб |
герб |
2-й исход |
герб |
надпись |
При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло. Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А). Таким образом, Р(A)=1/4; PB(А)=1/2 Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы. т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий. События А1, А2, ..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.
Лекция 3 Схема Бернулли
(Тема 2.2.)
План лекции
Формула полной вероятности.
Формула Байеса.
Повторение испытаний.
Формула Бернулли.
Локальная и интегральная формулы Муавра-Лапласа в схеме Бернулли.
Определение Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.
Теорема
Вероятность
события А,
наступающего совместно с гипотезами
Н1,
Н2,…,
Нп,
равна:
![]() где
p(Hi)
– вероятность i-
й гипотезы,
а p(A/Hi)
– вероятность события А
при условии реализации этой гипотезы.
Данная формула носит название формулы
полной вероятности.
где
p(Hi)
– вероятность i-
й гипотезы,
а p(A/Hi)
– вероятность события А
при условии реализации этой гипотезы.
Данная формула носит название формулы
полной вероятности.
Пример. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбранной урны наудачу вынут шар. Найти вероятность того, что он белый.
Решение.
Будем считать гипотезами Н1,
Н2
и Н3
выбор урны с соответствующим номером.
Так как по условию задачи все гипотезы
равновозможны, то
![]() Найдем условную вероятность А
при реализации каждой гипотезы:
Найдем условную вероятность А
при реализации каждой гипотезы:
![]()
![]() Тогда
Тогда
![]()
Формула Байеса (теорема гипотез).
Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Например, в предыдущем примере извлечение из урны белого шара говорит о том, что этой урной не могла быть третья, в которой нет белых шаров, то есть р (Н3/А) = 0. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса:
![]()
Пример. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.
Решение. Пусть событие А – одно попадание при двух выстрелах, а гипотезы: Н1 – первый попал, а второй промахнулся, Н2 – первый промахнулся, а второй попал, Н3 – оба попали, Н4 – оба промахнулись. Вероятности гипотез: р(Н1) = 0,6·0,3 = 0,18, р(Н2) = 0,4·0,7 = 0,28, р(Н3) = 0,6·0,7 = 0,42, р(Н4) = 0,4·0,3 = 0,12. Тогда р(А/Н1) = р(А/Н2) = 1, р(А/Н3) = р(А/Н4) = 0. Следовательно, полная вероятность р(А) = 0,18·1 + 0,28·1 + 0,42·0 + 0,12·0 = 0,46. Применяя формулу Байеса, получим:
![]()
Схема повторения испытаний. Формула Бернулли.
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.
Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рт,п того, что в результате п испытаний событие А наступило ровно т раз.
Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик)
Пусть в результате
п
независимых испытаний, проведенных в
одинаковых условиях, событие А наступает
с вероятностью Р(А)
= р, а
противоположное ему событие
с вероятностью
![]() .
.
Обозначим Ai – наступление события А в испытании с номером i. Т.к. условия проведения опытов одинаковые, то эти вероятности равны.
Если в результате
п
опытов событие А наступает ровно т
раз, то остальные п-т
раз это событие не наступает. Событие
А может появиться т
раз в п
испытаниях в различных комбинациях,
число которых равно количеству сочетаний
из п
элементов по т.
Это количество сочетаний находится по
формуле:
![]()
Вероятность каждой комбинации равна произведению вероятностей:
![]()
П рименяя
теорему сложения вероятностей несовместных
событий, получаем формулу
Бернулли:
рименяя
теорему сложения вероятностей несовместных
событий, получаем формулу
Бернулли:
![]()
Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.
Пример. Для получения приза нужно собрать 5 изделий с особым знаком на этикетке. Найти вероятность того, что придется купить 10 изделий, если этикетки с этим знаком имеют 5% изделий.
Решение.
Из постановки задачи следует, что
последнее купленное изделие имеет
особый знак. Следовательно, из предыдущих
девяти эти знаки имели 4 изделия. Найдем
вероятность этого по формуле Бернулли:
![]() Тогда
Тогда
р = 0,0006092·0,05 = 0,0000304.
Приближение Пуассона для схемы Бернулли.
Формула Бернулли требует громоздких расчетов при большом количестве испытаний. Можно получить более удобную для расчетов приближенную формулу, если при большом числе испытаний вероятность появления А в одном опыте мала, а произведение пр = λ сохраняет постоянное значение для разных серий опытов ( то есть среднее число появлений события А в разных сериях испытаний остается неизменным). Применим формулу Бернулли:
![]()
Найдем
предел полученного выражения при
![]()
![]()
Таким
образом, формула
Пуассона
![]() позволяет
найти вероятность к
появлений события А
для массовых (п
велико) и редких (р
мало) событий.
позволяет
найти вероятность к
появлений события А
для массовых (п
велико) и редких (р
мало) событий.
Теорема Муавра – Лапласа.
Теорема. (Теорема Муавра – Лапласа) Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то для любого интервала (, ) справедливо соотношение:
![]()
где Y
– число появлений события А в п опытах,
q
= 1 – p,
Ф(х) – функция
Лапласа,
![]() -
нормированная
функция Лапласа
.
-
нормированная
функция Лапласа
.
Теорема Муавра – Лапласа описывает поведение биноминального распределения при больших значениях п.
Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.
Расчет вероятности
попадания значения случайной величины
в заданный интервал
![]() при больших значениях п крайне
затруднителен. Гораздо проще воспользоваться
формулой:
при больших значениях п крайне
затруднителен. Гораздо проще воспользоваться
формулой:
![]()
Теорема Муавра – Лапласа очень широко применяется при решении практических задач.
Пример. Вероятность наступления события А в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что в 10000 испытаниях отклонение относительной частоты появления события А от его вероятности не превзойдет по абсолютной величине 0,01.
Пример. Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,96, можно было ожидать, что абсолютная величина отклонения относительной частоты годных деталей от вероятности детали быть годной, равной 0,98, не превысит 0,02.
Условие задачи фактически означает, что выполняется неравенство:
![]()
Здесь п- число годных деталей, т- число проверенных деталей. Для применения неравенства Чебышева преобразуем полученное выражение:
![]()
После
домножения выражения, стоящего в скобках,
на т получаем вероятность отклонения
по модулю количества годных деталей от
своего математического ожидания,
следовательно, можно применить неравенство
Чебышева, т.е. эта вероятность должна
быть не меньше, чем величина
![]() ,
а по условию задачи еще и не меньше, чем
0,96.
,
а по условию задачи еще и не меньше, чем
0,96.
Таким образом,
получаем неравенство
![]() .
Как уже говорилось в предыдущей задаче,
дисперсия может быть найдена по формуле
.
Как уже говорилось в предыдущей задаче,
дисперсия может быть найдена по формуле
![]() . Итого,
получаем:
. Итого,
получаем:
![]()
![]()
Т.е. для выполнения требуемых условий необходимо не менее 1225 деталей.
Пример. Суточная потребность электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 3000 кВт/час, а дисперсия составляет 2500. Оценить вероятность того, что в ближайшие сутки расход электроэнергии в этом населенном пункте будет от 2500 до 3500 кВт/час.
Требуется найти
вероятность попадания случайной величины
в заданный интервал:
![]()
Крайние значения интервала отклоняются от математического ожидания на одну и ту же величину, а именно – на 500. Тогда можно записать с учетом неравенства Чебышева:
![]()
Отсюда получаем:
![]()
Т.е. искомая вероятность будет не меньше, чем 0,99.
Пример. Вероятность того, что наудачу выбранная деталь окажется бракованной, при каждой проверке одна и та же и равна 0,2. Определить вероятность того, что среди 50 наугад выбранных деталей бракованных окажется не менее 6.
Для того, чтобы
воспользоваться теоремой Муавра -
Лапласа найдем математическое ожидание
и дисперсию количества бракованных
деталей в 50 – ти отобранных:![]()
Фактически в задаче требуется определить вероятность того, что бракованных деталей будет не менее шести, но и, очевидно, не более 50- ти.
![]() Значения
функции Лапласа находятся по таблице.
Конечно, значения функции Лапласа Ф(10)
в таблице нет, но т.к. в таблицах указано,
что Ф(3)=1,0000, то все значения от величин,
превышающих 3 также равны 1.
Значения
функции Лапласа находятся по таблице.
Конечно, значения функции Лапласа Ф(10)
в таблице нет, но т.к. в таблицах указано,
что Ф(3)=1,0000, то все значения от величин,
превышающих 3 также равны 1.
Пример. Известно, что 60% всего числа изготавливаемых заводом изделий являются изделиями первого сорта. Приемщик берет первые попавшиеся 200 изделий. Чему равна вероятность того, что среди них окажется из от 120 до 150 изделий первого сорта?
Вероятность того, что деталь окажется первого сорта, равна, очевидно, 0,6.Математическое ожидание числа изделий первого сорта равно:
![]()
По теореме Муавра - Лапласа получаем:
![]() Пример.
Проверкой установлено, что 96% изделий
служат не меньше гарантируемого срока.
Наугад выбирают 15000 изделий. Найти
вероятность того, что со сроком службы
менее гарантируемого будет от 570 до 630
изделий.
Пример.
Проверкой установлено, что 96% изделий
служат не меньше гарантируемого срока.
Наугад выбирают 15000 изделий. Найти
вероятность того, что со сроком службы
менее гарантируемого будет от 570 до 630
изделий.
Вероятность того, что срок службы изделия будет менее гарантированного равна: 1 – 0,96 = 0,04
Математическое
ожидание числа таких изделий равно
![]()
По теореме Муавра - Лапласа получаем:
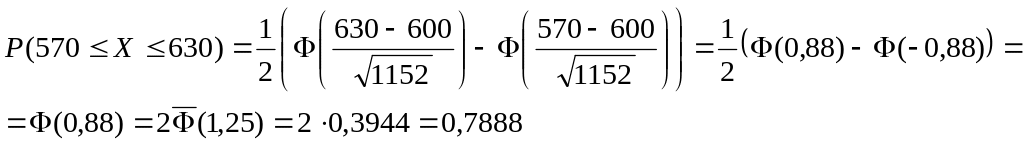
Лекция 4 Понятие ДСВ
(Тема 3.1.)
План лекции
Понятие случайной величины.
Понятие дискретной случайной величины.
Закон распределения.
Графическое изображение распределения ДСВ.
Независимые случайные величины.
Функция распределения, математическое ожидание, дисперсия и среднеквадратическое отклонение дискретной случайной величины.
Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.
Определение Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения – соответствующими малыми буквами (xi, yi,…).
Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.
Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно ( соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой – все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.
Определение Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Определение Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.
Дискретные случайные величины.
Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределения случайной величины. Он может иметь вид таблицы, формулы или графика.
Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения:
xi |
x1 |
x2 |
… |
xn |
… |
pi |
p1 |
p2 |
… |
pn |
… |
Заметим, что
событие, заключающееся в том, что
случайная величина примет одно из своих
возможных значений, является достоверным,
поэтому
![]()
Пример Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0,6 и 0,7. Составить ряд распределения случайной величины Х – числа попаданий после двух выстрелов.
Решение. Очевидно, что Х может принимать три значения: 0, 1 и 2. Их вероятности найдены в примере, рассмотренном в лекции 3. Следовательно, ряд распределения имеет вид:
хi |
0 |
1 |
2 |
pi |
0,12 |
0,46 |
0,42 |
Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (xi, pi).

x1 x2 x3 x4 x5
Функция распределения.
Определение Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х: F (x) = p (X < x). Свойства функции распределения.
0 ≤ F(x) ≤ 1. Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность.
Функция распределения является неубывающей функцией, то есть F(x2) ≥ F(x1) при х2 > x1. Это следует из того, что F(x2) = p(X < x2) = p(X < x1) + p(x1 ≤ X < x2) ≥ F(x1).
 В частности, если
все возможные значения Х лежат на
интервале [a,
b],
то F(x)
= 0 при х ≤ а и F(x)
= 1 при х ≥ b.
Действительно, X
< a
– событие невозможное, а X
< b
– достоверное.
В частности, если
все возможные значения Х лежат на
интервале [a,
b],
то F(x)
= 0 при х ≤ а и F(x)
= 1 при х ≥ b.
Действительно, X
< a
– событие невозможное, а X
< b
– достоверное.Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала: p ( a < X < b ) = F(b) – F(a).
Справедливость этого утверждения следует из определения функции распределения (см. свойство 2).
Для дискретной случайной величины значение F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.
Пример. Найдем F(x) для предыдущего примера:
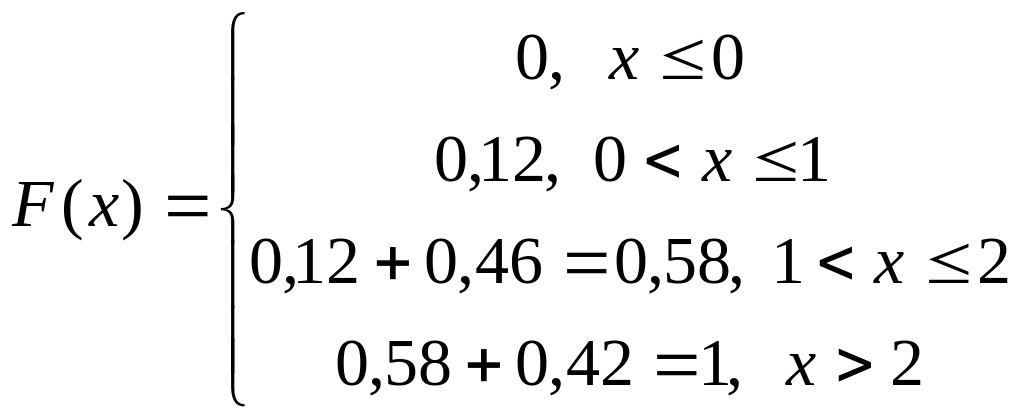
Соответственно график функции распределения имеет ступенчатый вид:





Определение Математическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:
М(Х)
= х1р1
+ х2р2
+ … + хпрп
.
![]() .
.
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непрерывных случайных величин.
Пример
1. Найдем математическое ожидание
случайной величины Х
– числа стандартных деталей среди трех,
отобранных из партии в 10 деталей, среди
которых 2 бракованных. Составим ряд
распределения для Х.
Из условия задачи следует, что Х
может принимать значения 1, 2, 3.
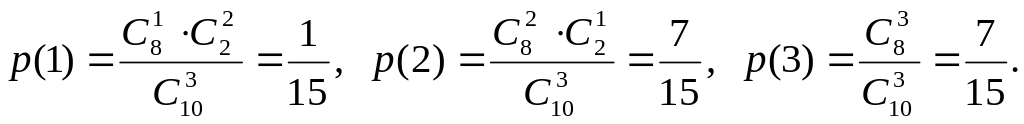
Тогда
![]()
Пример 2. Определим математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:
Х |
1 |
2 |
… |
п |
… |
р |
0,5 |
(0,5)2 |
… |
(0,5)п |
… |
Тогда
![]() ..+
..+
+![]() (при вычислении дважды использовалась
формула суммы бесконечно убывающей
геометрической прогрессии:
(при вычислении дважды использовалась
формула суммы бесконечно убывающей
геометрической прогрессии:
![]() ,
откуда
,
откуда
![]() ).
).
Свойства математического ожидания.
1. Математическое ожидание постоянной равно самой постоянной:
М(С) = С.
2. Постоянный множитель можно выносит за знак математического ожидания: М(СХ) = С М(Х).
Тогда М(СХ) = Сх1р1 + Сх2р2 + … + Схпрп = С( х1р1 + х2р2 + … + хпрп) = СМ(Х).
Определение Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.
Определение Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероятности равны произведениям вероятностей сомножителей.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) = M(X)M(Y). Следовательно, M(XY) = x1y1·p1g1 + x2y1·p2g1 + x1y2·p1g2 + x2y2·p2g2 = y1g1(x1p1 + x2p2) + + y2g2(x1p1 + x2p2) = (y1g1 + y2g2) (x1p1 + x2p2) = M(X)·M(Y).
Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.
Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.
Определение Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).
4. Математическое ожидание суммы двух случайных величин ( зависимых или независимых ) равно сумме математических ожиданий слагаемых: M (X + Y) = M (X) + M (Y).
Значит, M(X + Y) = x1p1 + x2p2 + y1g1 + y2g2 = M (X) + M (Y).
Замечание. Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.
Найдем математическое
ожидание числа очков, выпавших при
броске одной кости: М(Х1)
= (1 + 2 + 3 + 4 + 5 + 6)![]() Тому же числу равно математическое
ожидание числа очков, выпавших на любой
кости. Следовательно, по свойству 4
М(Х)=
Тому же числу равно математическое
ожидание числа очков, выпавших на любой
кости. Следовательно, по свойству 4
М(Х)=![]()
Дисперсия.
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
Х |
49 |
50 |
51 |
р |
0,1 |
0,8 |
0,1 |
Y |
0 |
100 |
p |
0,5 |
0,5 |
Найдем М(Х) = 49·0,1 + 50·0,8 + 51·0,1 = 50, М(Y) = 0·0,5 + 100·0,5 = 50. Как видно, математические ожидания обеих величин равны, но если для Х М(Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М(Y). Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Определение Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D(X) = M (X – M(X))².
Пример.
Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможного значения от математического ожидания:
(1 – 2,4)2 = 1,96; (2 – 2,4)2 = 0,16; (3 – 2,4)2 = 0,36. Следовательно,
![]()
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.
Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.
Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:
Теорема D(X) = M(X ²) – M ²(X). Доказательство.
Используя то, что М(Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:
D(X) = M(X – M(X))² = M(X² - 2X·M(X) + M²(X)) = M(X²) – 2M(X)·M(X) + M²(X) =
= M(X²) – 2M²(X) + M²(X) = M(X²) – M²(X), что и требовалось доказать.
Пример. Вычислим дисперсии случайных величин Х и Y, рассмотренных в начале этого раздела. М(Х) = (492·0,1 + 502·0,8 + 512·0,1) – 502 = 2500,2 – 2500 = 0,2.
М(Y) = (02·0,5 + 100²·0,5) – 50² = 5000 – 2500 = 2500. Итак, дисперсия второй случайной величины в несколько тысяч раз больше дисперсии первой. Таким образом, даже не зная законов распределения этих величин, по известным значениям дисперсии мы можем утверждать, что Х мало отклоняется от своего математического ожидания, в то время как для Y это отклонение весьма существенно.
Свойства дисперсии.
Дисперсия постоянной величины С равна нулю: D (C) = 0.
Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D(CX) = C²D(X).
Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(X + Y) = D(X) + D(Y).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X – Y) = D(X) + D(Y).
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.
Определение
Средним
квадратическим отклонением
σ случайной величины Х
называется квадратный корень из
дисперсии:
![]() .
.
Пример. В предыдущем
примере средние квадратические отклонения
Х
и Y
равны соответственно
![]()
Лекция 5 Распределения ДСВ
(Тема 3.2.)
План лекции
Понятие биномиального распределения.
Характеристики биномиального распределения.
Понятие геометрического распределения.
Характеристики геометрического распределения.
Биномиальное распределение.
Вернемся к схеме независимых испытаний и найдем закон распределения случайной величины Х – числа появлений события А в серии из п испытаний. Возможные значения А: 0, 1, …, п. Соответствующие им вероятности можно вычислить по формуле Бернулли:
![]() (
p
– вероятность появления А в каждом
испытании).
(
p
– вероятность появления А в каждом
испытании).
Такой закон
распределения называют биномиальным,
поскольку правую часть равенства можно
рассматривать как общий член разложения
бинома Ньютона:
![]()
Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний, М(Х) можно найти, используя свойство математического ожидания. Пусть Х1 – число появлений А в первом испытании, Х2 – во втором и т.д. При этом каждая из случайных величин Хi задается рядом распределения вида
Xi |
0 |
1 |
pi |
q |
p |
Следовательно,
М(Хi)
= p.
Тогда
![]()
Аналогичным образом
вычислим дисперсию: D(Xi)
= 0²·q
+ 1²·p
– p²=
p
– p²
= p(1
– p),
откуда по свойству 4 дисперсии
![]()
Пример. Составим ряд распределения случайной величины Х – числа попаданий при 5 выстрелах, если вероятность попадания при одном выстреле равна 0,8.
р(Х=0) = 1·(0,2)5 = 0,00032; р(Х=1) = 5·0,8·(0,2)4 = 0,0064; р(Х=2) = 10·(0,8)2·(0,2)3 = 0,0512; р(Х=3) = 10·(0,8)3·(0,2)2 = 0,2048; р(Х=4) = 5·(0,8)4·0,2 = 0,4096; р(Х=5) = 1·(0,8)5 = 0,32768. Таким образом, ряд распределения имеет вид:
х |
0 |
1 |
2 |
3 |
4 |
5 |
р |
0.00032 |
0.0064 |
0.0512 |
0.2048 |
0.4096 |
0.32728 |
Пример. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.
Вероятность появления нестандартной детали в каждом случае равна 0,1.
Найдем вероятности того, что среди отобранных деталей:
1) Вообще
нет нестандартных.
![]()
2) Одна
нестандартная.
![]()
3) Две
нестандартные детали.
![]()
4) Три
нестандартные детали.
![]()
5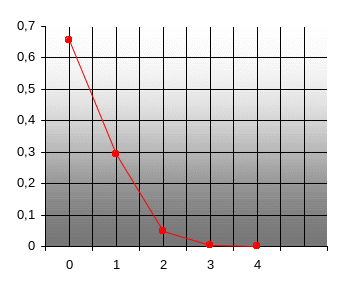 )
Четыре
нестандартных детали.
)
Четыре
нестандартных детали.
![]()
Построим многоугольник распределения.
Пример. Две игральные кости одновременно бросают 2 раза. Написать биноминальный закон распределения дискретной случайной величины Х – числа выпадений четного числа очков на двух игральных костях.
Каждая игральная кость имеет три варианта четных очков – 2, 4 и 6 из шести возможных, таким образом, вероятность выпадения четного числа очков на одной кости равна 0,5.
Вероятность одновременного выпадения четных очков на двух костях равна 0,25.
Вероятность того,
что при двух испытаниях оба раза выпали
четные очки на обеих костях, равна:
![]()
Вероятность того,
что при двух испытаниях один раз выпали
четные очки на обеих костях:
![]()
Вероятность того,
что при двух испытаниях ни одного раза
не выпаде четного числа очков на обеих
костях:
![]()
Лекция 6 Непрерывная случайная величина
(Тема 4.1.)
План лекции
Понятие непрерывной случайной величины.
Функция плотности непрерывной случайной величины: определение, свойства.
Интегральная функция распределения непрерывной случайной величины: определение, свойства, её связь с функцией плотности.
Методика расчета вероятностей для НСВ по её функции плотности и интегральной функции распределения.
Математическое ожидание, дисперсия и среднеквадратическое отклонение. Медиана и мода непрерывной случайной величины.
Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р(Х = а) = F(a) – F(a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал.
Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифференциальная функция).
Определение 5.1. Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле:
f (x) = F′(x), (5.1)
то есть является производной функции распределения.
Свойства плотности распределения.
f(x) ≥ 0, так как функция распределения является неубывающей.
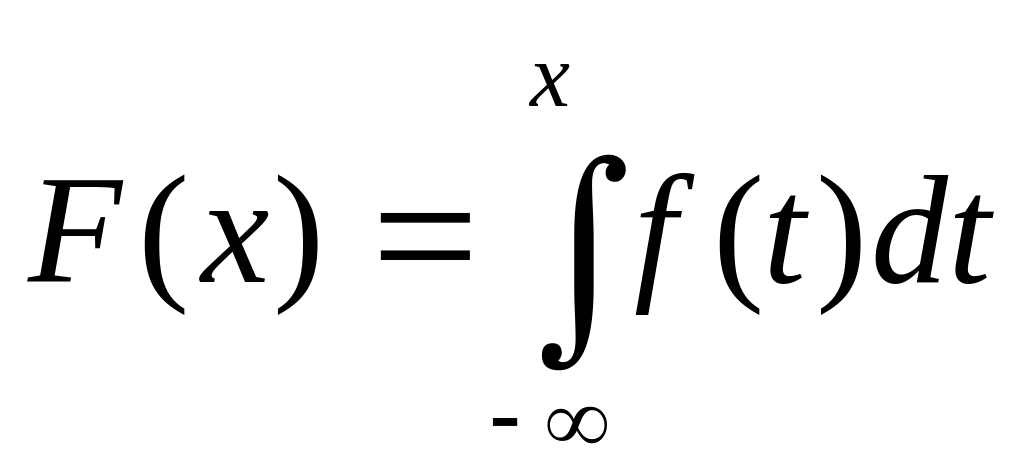 ,
что следует из определения плотности
распределения.
,
что следует из определения плотности
распределения.Вероятность попадания случайной величины в интервал (а, b) определяется формулой
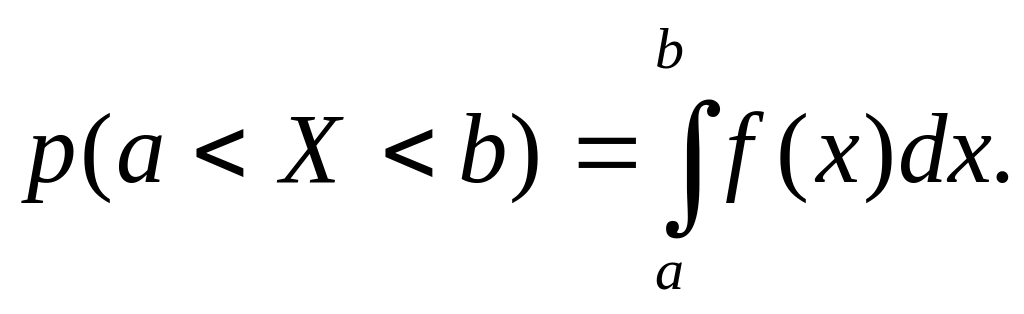 Действительно,
Действительно,

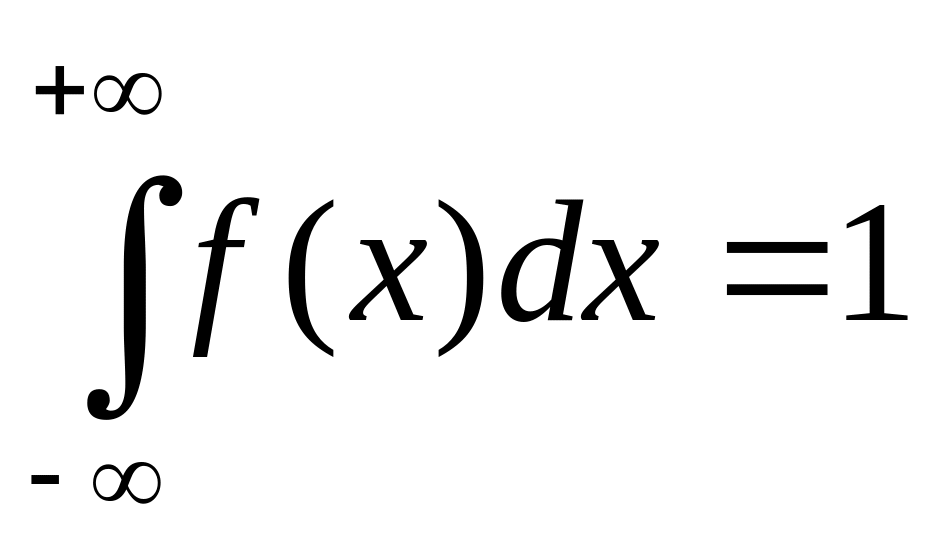 (условие нормировки).
Его справедливость следует из того,
что
(условие нормировки).
Его справедливость следует из того,
что
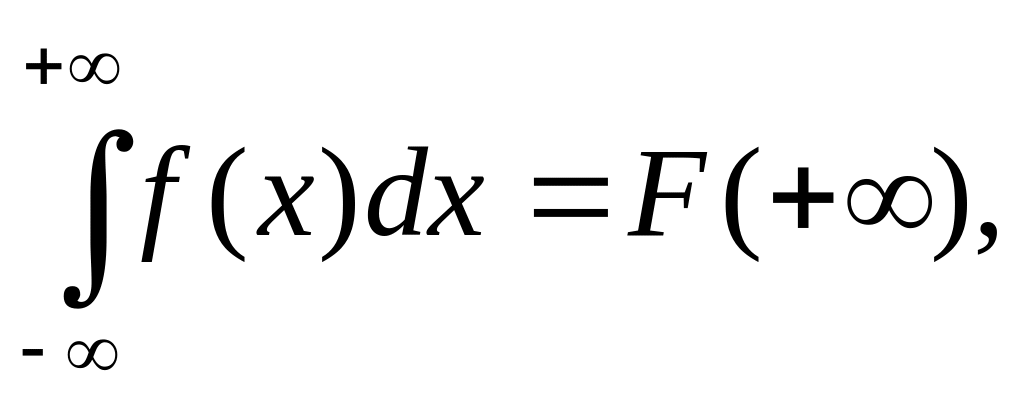 а
а

 так как
так как
 при
при

Таким образом,
график плотности распределения
представляет собой кривую, расположенную
выше оси Ох,
причем эта ось является ее горизонтальной
асимптотой при
![]() (последнее справедливо только для
случайных величин, множеством возможных
значений которых является все множество
действительных чисел). Площадь
криволинейной трапеции, ограниченной
графиком этой функции, равна единице.
(последнее справедливо только для
случайных величин, множеством возможных
значений которых является все множество
действительных чисел). Площадь
криволинейной трапеции, ограниченной
графиком этой функции, равна единице.
Замечание. Если все возможные значения непрерывной случайной величины сосредоточены на интервале [a, b], то все интегралы вычисляются в этих пределах, а вне интервала [a, b] f(x) ≡ 0.
Пример 1.
Плотность распределения непрерывной
случайной величины задана формулой
![]()
Найти: а) значение константы С; б) вид функции распределения; в) p(-1 < x < 1).
Решение. а) значение константы С найдем из свойства 4:
![]() откуда
откуда
![]() .
.
б)
![]()
в)
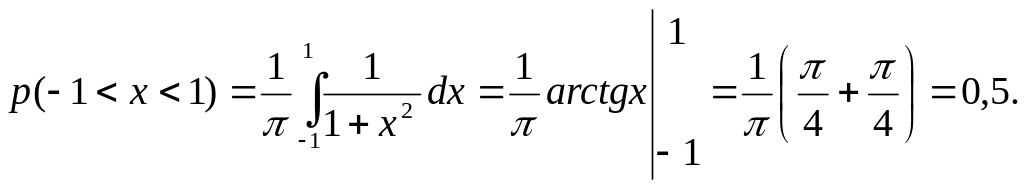
Пример 2. Функция распределения непрерывной случайной величины имеет вид:
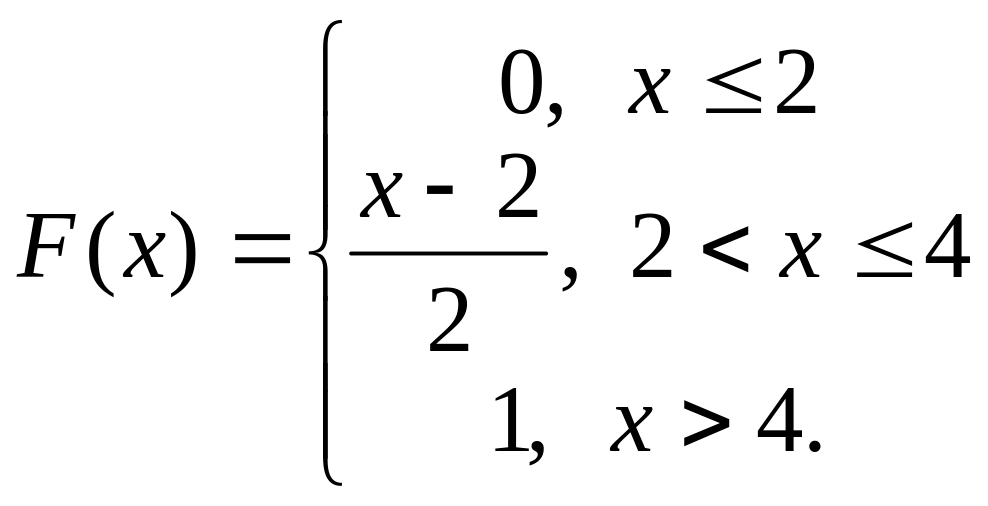
Найти плотность распределения.
Решение.
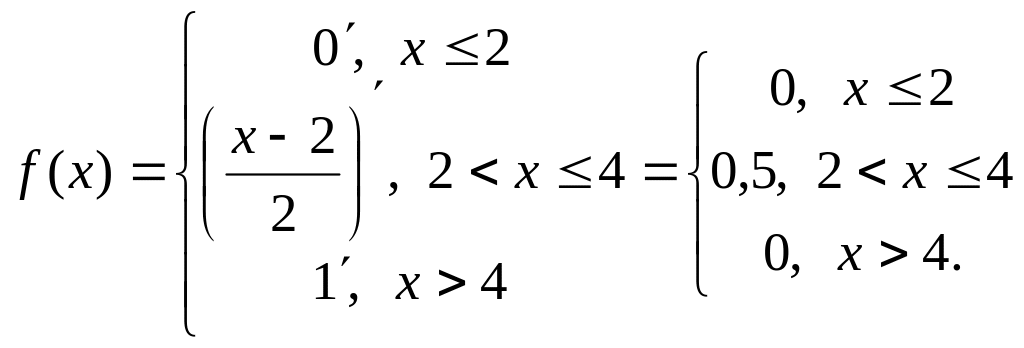
Пример 3. Могут ли функции (x) и (x) являться ФР или ПР некоторой СВ X, если “да”, то при каком значении ?
а) (x)
=
![]()
б) (x)
=

Различают следующие группы числовых характеристик: характеристики положения (математическое ожидание, мода, медиана, квантиль и др.), рассеивания (дисперсия, среднеквадратичное отклонение и др.), характеристики формы плотности распределения (показатель асимметрии, эксцесса и др.).
Числовые характеристики непрерывных случайных величин.
Распространим определения числовых характеристик случайных величин на непре-рывные случайные величины, для которых плотность распределения служит в некото-ром роде аналогом понятия вероятности.
Определение.
Математическим
ожиданием
(средним значением по распределению)
называется действительное число,
определяемое в зависимости от типа СВ
Х
формулой: mX
= M[X]
=

Для непрерывной
случайной величины называется
![]() Замечание
1. Общее
определение дисперсии сохраняется для
непрерывной случайной величины таким
же, как и для дискретной, а формула для
ее вычисления имеет вид:
Замечание
1. Общее
определение дисперсии сохраняется для
непрерывной случайной величины таким
же, как и для дискретной, а формула для
ее вычисления имеет вид:
![]() Среднее
квадратическое отклонение вычисляется
по формуле
Среднее
квадратическое отклонение вычисляется
по формуле
Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [a, b], то интегралы в формулах и вычисляются в этих пределах.
Пример. Плотность распределения случайной величины Х имеет вид:

Найти М(Х), D(X), σ.
Решение.

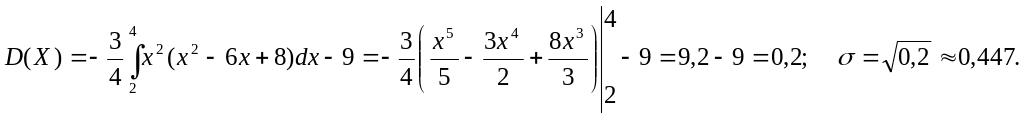 Свойства
математического ожидания:
Свойства
математического ожидания:
M[C] = C, где С - константа;
M[CX] = CM[X];
M[X+Y] = M[X]+M[Y], для любых СВ X и Y;
M[XY] = M[X]M[Y] + KXY, где KXY = M[
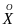
 ]
- ковариация СВ X
и Y.
]
- ковариация СВ X
и Y.
Начальным моментом k-го порядка (k = 0, 1, 2, ...) распределения СВ Х называется действительное число, определяемое по формуле:
k
= M[Xk]
=

Центральным моментом k-го порядка распределения СВ Х называется число, определяемое по формуле:
k
= M[(X-mX)k]=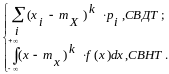
Из определений моментов, в частности, следует, что: 0 = 0 = 1, 1 = mX, 2 = DX = X2.
Модой СВНТ называется действительное число Mo(X) = x*, определяемое как точка максимума ПР f(x). Мода может иметь единственное значение (унимодальное распределение) или иметь множество значений (мультимодальное распределение).
Медианой СВНТ называется действительное число Mе(X) = x0, удовлетворяющее условию: P{X x0} = P{X x0} или F(x0) = 0,5.
Квантилем уровня р называется действительное число tp, удовлетворяющее уравнению: F(tp) = p. В частности, из определения медианы следует, что x0 = t0,5.
Дисперсией СВ Х называется неотрицательное число D[X] = DХ, определяемое формулой:
DX
= M[(X-mX)2]
= M[X2]
- mX2
=
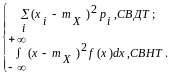
Дисперсия существует, если ряд (соответственно интеграл) в правой части равенства сходится. Свойства дисперсии:
D[C] = 0, где С - константа;
D[CX] = C2D[X];
D[X-C] = D[X], дисперсия, очевидно, не меняется от смещения СВ X;
D[X + Y] = D[X] + D[Y] + 2KXY, где KXY = M[ ] - ковариация СВ X и Y;
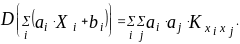
Неотрицательное
число Х
=
![]() называется среднеквадратичным
отклонением
СВ X.
Оно имеет размерность СВ Х и определяет
некоторый стандартный среднеквадратичный
интервал рассеивания, симметричный
относительно математического ожидания.
(Величину Х
иногда называют стандартным отклонением).
СВ Х называется стандартизованной,
если mX
= 0 и
Х
= 1. Если
величина Х
= const
(т.е. Х не случайна), то D[X]
= 0.
называется среднеквадратичным
отклонением
СВ X.
Оно имеет размерность СВ Х и определяет
некоторый стандартный среднеквадратичный
интервал рассеивания, симметричный
относительно математического ожидания.
(Величину Х
иногда называют стандартным отклонением).
СВ Х называется стандартизованной,
если mX
= 0 и
Х
= 1. Если
величина Х
= const
(т.е. Х не случайна), то D[X]
= 0.
Показателем асимметрии ПР является коэффициент асимметрии (“скошенности”) распределения: A = 3/3X. Показателем эксцесса ПР является коэффициент эксцесса (“островершинности”) распределения: E = (4/4X)-3. В частности, для нормального распределения E = 0.


Лекция 7 Распределения НСВ
(Тема 4.2.)
План лекции
Понятие равномерно распределенной НСВ.
Геометрическое определение вероятности.
Функция плотности и свойства равномерно распределенной НСВ. Определение и функция плотности нормально распределенной НСВ.
Кривая Гаусса и её свойства.
Смысл параметров нормального распределения.
Интегральная функция распределения нормально распределенной НСВ. Определение и функция плотности показательно распределенной НСВ. Интегральная функция распределения показательно распределенной НСВ. Характеристики показательно распределенной НСВ.
