
- •1. Принцип управления. Классификация систем управления.
- •Принцип разомкнутого управления
- •Принцип регулирования по отклонению
- •2. Алгоритмы и законы регулирования
- •3. Математическое описание сау. Модели вход-выход.
- •4. Математическое описание сау. Модели вход-состояние-выход.
- •5. Математическое описание звеньев и сау. Типовые звенья.
- •6. Типовые воздействия в системе и реакция на них.
- •7. Устойчивость систем управления. Первый метод Ляпунова.
- •8. Устойчивость систем управления. Частотный критерий устойчивости.
- •9. Устойчивость систем управления. Алгебраические критерии устойчивости.
- •10. Качество установившихся процессов в линейных сау. Коэффициенты ошибок.
- •Способы устранения статической ошибки.
- •Коэффициенты ошибок
- •11. Качество установившихся процессов в линейных сау. Частотные критерии качества.
- •12. Качество установившихся процессов в линейных сау. Корневые критерии качества.
- •13. Качество установившихся процессов в линейных сау. Интегральные критерии качества.
- •14. Коррекция сау. Способы коррекции.
- •15. Коррекция сау в функции внешних воздействий. Инвариантность.
- •Коррекция по возмущающему воздействию
- •16. Задачи и методы синтеза лмнейных сау.
- •17. Многомерные сау.
- •18. Чувствительность систем управления.
- •Существуют методы анализа чувствительности и методы достижения малой чувствительности в проектируемых системах.
- •Определить чувствительность для системы:
- •Управляемость.
- •20. Наблюдаемость систем управления.
- •Наблюдаемость.
- •21. Дискретные системы управления. Классификация.
- •22. Импульсные системы управления.
- •23. Нелинейные системы управления. Второй метод Ляпунова.
- •24. Автоколебания нелинейных сау. Определение параметров автоколебаний.
- •Определение параметров автоколебаний
- •25. Методы линеаризации нелинейных сау.
- •26. Случайные процессы
- •Прохождение случайного сигнала через линейную систему.
- •27. Оптимальное управление. Постановка задачи оптимального управления. Критерии оптимальности.
- •28. Аналитическое конструирование регуляторов. Постановка задачи.
- •29. Методы теории оптимального управления
- •30. Адаптивные системы управления. Классификация адаптивных сау.
8. Устойчивость систем управления. Частотный критерий устойчивости.
Устойчивость – свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия. Это свойство затухания переходного процесса с течением времени.
Для тех объектов, которые работают в условиях непрерывно меняющихся воздействий, т.е. когда установившийся режим вообще отсутствует, дается общее определение устойчивости:
Система устойчива, если её выходная величина остаётся ограниченной в условиях действия на систему ограниченных по величине возмущений.
Yсв →0 при t→∞ , если все корни характеристического уравнения λ обладают отрицательной вещественной частью.
Если хотя бы один вещественный корень λi будет положительным или хотя бы одна пара комплексно-сопряженных корней будет иметь положительную вещественную часть, то в этом случае процесс будет расходящийся.
Если в характеристическом уравнении системы имеется хотя бы один нулевой корень или хотя бы одна пара чисто мнимых корней λi,i+1 = +jβ , то система будет находиться на границе устойчивости.
![]()
Критерий Михайлова. Это частотный критерий и он позволяет судить об устойчивости замкнутой системы.
D(λ) = a0*λn + a1*λn -1 +…+ an -1*λ + an . Считать все коэффициенты характеристического уравнения положительными.
Если вместо λ подставить jω, то D(jω) = X(ω) + jY(ω)
X(ω) = an + an –2*ω2 +… (четные степени ω)
Y(ω) = an –1* ω + an –3*ω3 +… (нечетные степени ω)
При ω=0, X=an , Y=0
При ω→0, X=∞(-∞), Y=∞(-∞) («+» или «-» зависит от степени n)
n=3, X= -∞, Y= -∞
n=5, X= ∞, Y= ∞
Если изменять ω от 0 до ∞, то D(jω) будет описывать некоторую траекторию, которая будет называться годографом Михайлова.
Д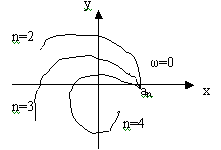 ля
устойчивости линейной системыn-порядка
необходимо и достаточно, чтобы изменение
аргумента функции D(jω)
изменении ω
от 0 до ∞ = n*π/2
ля
устойчивости линейной системыn-порядка
необходимо и достаточно, чтобы изменение
аргумента функции D(jω)
изменении ω
от 0 до ∞ = n*π/2
![]()
Другими словами требуется, чтобы кривая Михайлова проходила последовательно n-квадрантов против часовой стрелки, все время огибая начало координат.
Если годограф проходит через начало координат, то система находится на границе устойчивости.
Если нарушается процесс обхода, то система не устойчива.
Для того чтобы система была устойчивой необходимо, чтобы нули X и Y чередовались с ростом ω, начиная с ω=0.
X(ω)=0 Y(ω)=0
|
X |
an |
0 |
|
0 |
|
0 |
|
Y |
0 |
|
0 |
|
0 |
|
Д ля
того, чтобы определить границы
устойчивости, необходимо решить системы:
ля
того, чтобы определить границы
устойчивости, необходимо решить системы:
X(ω)=0
Y(ω)=0
Критерий устойчивости Найквиста.
![]() Он
базируется на частотных характеристиках
разомкнутой цепи САУ. Он дает правило,
согласно которым по виду частотной
характеристики разомкнутой цепи можно
судить об устойчивости замкнутой
системы. W(jω)
→ Ф(jω)
Он
базируется на частотных характеристиках
разомкнутой цепи САУ. Он дает правило,
согласно которым по виду частотной
характеристики разомкнутой цепи можно
судить об устойчивости замкнутой
системы. W(jω)
→ Ф(jω)
Формулировка критерия в зависимости от исходного состояния системы может быть различной.
Система устойчива в разомкнутом состоянии.

Критерий Найквиста: Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы н. и д. чтобы АФЧХ разомкнутой цепи не охватывала точку с координатами (-1; j0).
Система нейтральна в разомкнутом состоянии.
Т. е. характер. многочлен разомкнутой цепи L(S) имеет один нулевой корень, а все остальные корни имеют отрицательные вещественные части.
Формулировка критерия остается прежней, но при этом в число переходов надо включать пунктирный переход окружности бесконечного радиуса, дополняющий годограф до положительного направления вещественной оси.
Система не устойчива в разомкнутом состоянии.
Для устойчивости замкнутой системы требуется, чтобы АФЧХ разомкнутой системы охватывала т. с координатами (-1; j0)против часовой стрелки на угол lπ.(Другими словами требуется, чтобы левее т. (-1) разность отрицательных переходов АФЧХ через ось абсцисс = l/2, l – число правых корней характеристического многочлена).
