Формирование циклического кода.
Правило: нужно исходную кодовую комбинацию (КК) - Q(x) разделить на образующий полином Р(х) и дописать справа остаток от деления к исходной КК.
Обозначим F(x) – комбинация циклического кода.
F(x)
= Q(x)
*x
k
R(x)
, где k
– степень образующего полинома.
Величина k показывает количество сдвигов влево, которое Q(x) должно претерпеть.
Пример: Q(x) = x 5 + x 3 + x = 101010 – исходная КК,
Р(х) = x 3 + x + 1 = 1011 - образующий полином
R(x) = x 2 + x = 110 - полученный остаток от деления,
F(x) = 101010 110 - комбинация циклического кода,
где: 101010 - информационная часть, 110 – контрольная часть
Остаток R(x) называется синдромом..
Пусть Q(x) = 1110. Если k =3, то Q(x) X k = 1110 000
Проверка правильности циклического кода.
Правильность циклического кода проверяется с помощью операции деления на образующий полином. Если в результате деления остаток равен нулю (R(x)=0), то считается ,что комбинация циклического кода ошибки не содержит.Если же при делении получился остаток, то комбинация содержит ошибку, которую можно исправить. Процедура отыскания места ошибки сводится к циклическим сдвигам КК F(х) и деление ее на образующий полином.
W - вес остатка (количество единиц в нем).
S - кратность ошибки (количество ошибочных разрядов в кодовой комбинации).
В алгоритме используются циклические сдвиги влево и вправо, количество которых подсчитывается во время выполнения.
Cn - счетчик циклических сдвигов.
10 Код Хэмминга.
Сущность кода Хэмминга заключается в том, что контрольные разряды, определяемые на основе информационной части, определяются с помощью вычисления контрольных сумм по модулю 2. Для каждого контрольного разряда своя контрольная сумма. Контрольные разряды могут размещаться как справа информационной части, так и внутри нее.
В коде Хэмминга используется не менее трех контрольных разрядов, каждый из которых определяется путем проверки на четность. Проверка происходит для определенных групп рабочих разрядов.
Используются два варианта размещения контрольных разрядов:
1.контрольные разряды располагаются отдельно от информационных;
2.контрольные разряды чередуются с информационными.
Позиции контрольных разрядов:
|
...X12 |
X11 |
X10 |
X9 |
X8 |
X7 |
X6 |
X5 |
X4 |
X3 |
X2 |
X1 |
|
... И |
И |
И |
И |
К |
И |
И |
И |
К |
И |
К |
К |
К - контрольный разряд, И - информационный разряд.
Место контрольного разряда определяется формулой: 2i =1,2,4,8,16,...
где i – номер контрольного разряда.
Условия проверки на четность.
Для определения контрольных разрядов используется сумма по модулю 2 (проверка на четность). Количество условий проверки на четность равно количеству контрольных разрядов. Эти условия сводятся к вычислению контрольных сумм: S1,S2,S3...
через 1 по 1
через 2 по 2
через 4 по 4
Вычисление 1-ого
контрольного разряда:
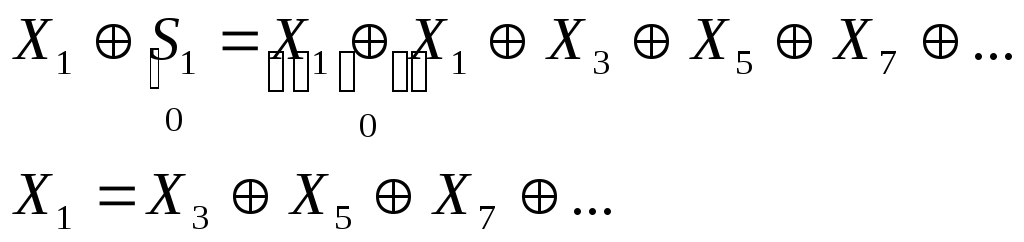
Вычисление
2-ого контрольного разряда:
Вычисление
3-его контрольного разряда:
Условия проверки на четность позволяют установить место ошибочного разряда ( обнаружить и устранить ошибку ).
Опознаватель места ошибки – это кодовая комбинация, составленная из контрольных сумм: S0=...S4,S3,S2,S1 , где S0 - число, указывающее на номер ошибочного разряда. Если S0=0, то ошибки в кодовой комбинации нет.
Для исправления ошибки необходимо заменить 0 на 1 и наоборот.
Пример. Закодируем кодом Хэмминга число 11.
Q(X)=(1011)2=(11)10 – безызбыточный код.
Определение мест информационных разрядов.
-
И
К
И
И
И
К
И
К
К
--
--
1
0
1
0
1
0
1
Вычисление контрольных разрядов.
Результат : H(X)=1010101 – код Хемминга.
Обнаружение и исправление ошибок.
Пусть Hош (X)=1011101
Определим место ошибочного разряда путем вычисления контрольных сумм.
Опознаватель S0 = 100, т. е. ошибка в 4-ом разряде.
Определение количества контрольных разрядов в коде Хэмминга.
Для определения количества контрольных разрядов необходимо, чтобы выполнялось следующее условие: опознаватель ошибки S должен указать любой по порядку ошибочный разряд.
Если
,
тоS0
= 000...111 можно найти ошибку в 7 разрядах.
Если
,
тоS0
= 0000...1111,
т.е. ошибка обнаруживается в 15-ти
разрядном коде.
,
то S0
= 00000...11111
(11111)2 = (31)10
Общая связь:
или
Существуют коды, которые позволяют обнаружить более одной ошибки. Это дается ценой увеличения избыточности (контрольных разрядов).
При применении кода Хэмминга не снимается проблема борьбы с групповыми ошибками, т.е. ошибочно 2 или большее количество рядом стоящих разрядов.