
- •1. Погрешности абсолютные, относительные, приведенные. Суммирование погрешностей.
- •2. Нормирование погрешностей средств измерения.
- •3. Погрешности косвенных измерений. Классы точности измерительных приборов.
- •4. Систематические погрешности. Случайные погрешности. Законы распределения случайных погрешностей. Определение доверительных границ погрешностей для нормального закона распределения.
- •5. Временное уплотнение сигналов. Временная диаграмма, структурная схема.
- •6 Способы многоканальной передачи сигналов.Частотное уплотненение.Структурная схема.
- •7.Проводные линии связи. Эквивалентная схема. Первичные и вторичные параметры.
- •7.2 Вторичные параметры линии.
- •8. Каналы связи в телемеханике.
- •9. Циклические коды.
- •Формирование циклического кода.
- •10 Код Хэмминга.
- •11. Частотный спектр импульсного сигнала.
- •Частоты гармоник:
- •Амплитуды гармоник.
- •12Способы импульсной модуляции (им).
- •13 Частотная модуляция (чм).
- •14 Способы модуляции электрических сигналов.
- •15 Способы интерполяции сигнала, квантованного по времени.
- •16 Квантование по времени.
- •Выбор времени цикла Тц
- •17 Квантование по уровню.
1. Погрешности абсолютные, относительные, приведенные. Суммирование погрешностей.
Результат измерений включает различные погрешности:
Хк - истинное значение измеряемой величены
Х - показание прибора
1. Абсолютная погрешность - X-Xи (разность между показанием прибора и истинным значением измеряемой величины). Истинное значение неизвестно и мы примем за него действительное значение X-Xд. За Хд принимают показания образцовых приборов. В качестве образцовых могут быть выбраны приборы класс точности которых составляет не более 1/3 класса точности поверяемых.
2.
Относительная погрешность
-
![]()
3.
Приведенная
погрешность
-
![]() ,
где Хк
- конечное значение диапазона измерений
,
где Хк
- конечное значение диапазона измерений
4. Инструментальная принадлежит данному средству измерения. Их можно определить при испытании и занести в паспорт прибора. Они определяются несовершенством конструкции и технологии, износом и т.д.(например, порог чувствительности в сравнивающих устройствах, неточность резистивных делителей, неточность градуировки шкалы и т.д.).
5. Методические – связаны с методом применения прибора(например, измерение напряжения вольтметром с конечным сопротивлением).

6. Основные возникают при нормальных условиях эксплуатации. Эти условия записаны в паспорте на прибор (например, tокр.ср.=25+5оС, Uпит, f, атмосферное давление, наличие тряски, вибрации и т.д.). По основным погрешностям чаще всего устанавливают класс точности прибора.
7. Дополнительные возникают при отклонении условий эксплуатации от нормальных. Они задаются коэффициентом влияния (например, класс точности преобразователя давления 1.0 на 10 оС).
8. Аддитивная и мультипликативная.
Если снимать характеристику любого средства измерения y=f(x), то мы получим не одну прямую, а полосу. Для характеристики формы этой полосы и ввели понятие аддитивной и мультипликативной погрешностей.
Зависимость
вых. величины от входной.
Maxзначение абсолютной погрешности не
превосходит постоянной величины+.
Maxзначение абсолютной величины прямо
пропорциональна измеряемой величине.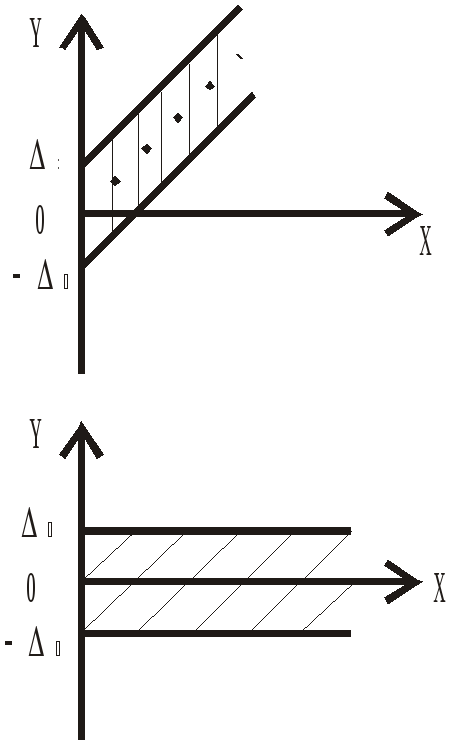

аддитивная мультипликативная
9. Систематические – постоянные или закономерно изменяющиеся погрешности. Их основной отличительный признак: они могут быть предсказаны и почти полностью удалены введением поправок.
10. Постоянные – можно обнаружить при поверке по образцовым мерам и сигналам.
11. Закономерно изменяющиеся – большинство дополнительных погрешностей.
12. Прогрессирующие – непредсказуемые погрешности медленно изменяющиеся во времени. Они вызываются старением деталей. Их можно скорректировать только на данный момент времени.
13. Случайные – непредсказуемые ни по знаку ни по величине. Их можно обнаружить при повторных измерениях в виде разброса результата измерения. Описание случайных погрешностей проводят на основе теории вероятности.
1
Пример для
цифрового вольтметра последовательного
счета. Х – аналоговый
вход, q– шаг квантования. Х сравнивается
с известной величиной Хкiскачками в один квантq. Хк=q Определение
уровня происходит при выполнении
условия Хк>Х, т.е. в какой-то
момент времени Хкi-Х=Хк,
гдеможет быть от 0 до1, т.е. погрешность .![]()

Суммирование погрешностей.
Определение оценки результата погрешности по известным оценкам ее составляющих называется суммированием погрешностей. Все составляющие погрешностей рассматриваются, как случайные величины. Результирующую погрешность находят в виде дроби c/d или к/н
1. Все погрешности делят на аддитивные и мультипликативные. Находят приведенную погрешность в начале шкалы, т.е. н при Х=0, суммируют все аддитивные составляющие.
2. Учитывается взаимная корреляция. Если случайные величины (погрешности) не коррелированны, то результирующую погрешность находят как их сумму
![]() .
Если погрешности коррелированны, то
они суммируются алгебраически с учетом
знаков
.
Если погрешности коррелированны, то
они суммируются алгебраически с учетом
знаков
![]() ,
,
![]() .
После того, как коррелированные
погрешности выделены и среди них
проведены алгебраические сложения,
суммарные по группам и оставшиеся
погрешности суммируются геометрически.
.
После того, как коррелированные
погрешности выделены и среди них
проведены алгебраические сложения,
суммарные по группам и оставшиеся
погрешности суммируются геометрически.
При Х=Хк
суммируются все погрешности (ад. и
мульт.)
![]()
Обычно
законы распределения неизвестны и для
определения доверительной вероятности
используют Pд=0.9,
т.е.
![]() ,
,
т.к. коэффициент будет постоянен и для результата измерения и для результата погрешности, то можно суммировать просто относительные погрешности. Принимаем i0.9=max=1.0%
![]()
![]()
![]()
