4.5. Векторные пространства и линейные алгебры

Множество V называется векторным пространством над полем , если для него выполняются следующие аксиомы:

Аксиома V.1. Множество является абелевой аддитивной группой.

Аксиома V.2. Для любого вектора и любого элемента поля определено произведение , являющееся вектором (элементы поля называются скалярами, а элементы – векторами).

Аксиома V.3 (дистрибутивный закон). Если и – векторы из множества , а – скаляр, то .

Аксиома V.4 (дистрибутивный закон). Если – вектор, а и – скаляры, то .

Аксиома V.5 (ассоциативный закон). Если – вектор, а и – скаляры, то и .

Множество называется линейной ассоциативной алгеброй над полем , если выполняются следующие аксиомы:

Аксиома A.1. Множество является векторным пространством над .

Аксиома A.2. Для любых двух элементов и из существует произведение 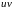, определяемое как некоторый элемент из .

Аксиома A.3 (ассоциативный закон). Для любых трех элементов и из справедливо равенство .

Аксиома A.4 (билинейный закон). Если и – скаляры из , а и – векторы из , то и .

Набором длины элементов поля называется упорядоченное множество из элементов поля, обозначаемое как , где каждый из является элементом поля. Сложение наборов длины определяется следующим образом:

.

Умножение наборов длины на элемент поля определяется правилом:

.

Если определены две операции (сложение и умножение), то совокупность всех наборов длины над полем образует векторное пространство.

Пример: GF(2)={0,1}

, , , .

Все операции осуществляются по модулю 2.

; .

Единичный элемент векторного пространства обозначается как нулевой вектор O = (0, 0, 0, …, 0).

Подмножество векторного пространства называется подпространством, если оно удовлетворяет аксиомам векторного пространства.

Пример:

Пространство 000, 001, 010, 011, 100, 101, 110, 111 содержит следующее подпространство: 000, 001, 010, 011.

Линейной комбинацией k векторов v₁, v₂, …, v_k называется сумма вида:

,

где a_i – скаляры, т.е. элементы поля.

Теорема 1. Совокупность всех линейных комбинаций некоторого набора векторов v₁, …, v_k из векторного пространства V является подпространством пространства V.

Пример:

000-0

001-v₁

010-v₂

011-v₃

100-v₄

101-v₅

110-v₆

111-v₇

Линейные комбинации векторов генерируют все пространство:

0 – нулевая комбинация, , , , , .

Совокупность векторов v₁, v₂, …, v_k называется линейно зависимой тогда и только тогда, когда существуют скаляры c₁, c₂, …, c_k, не все равные нулю, такие, что

.

Совокупность векторов называется линейно независимой, если она не является линейно зависимой.

Теорема 2. Если совокупность k векторов v₁, …, v_k порождает векторное пространство, которое содержит некоторую совокупность из m линейно независимых векторов u₁, , u_m, то .

Теорема 3. Если два множества линейно независимых векторов порождают одно и то же пространство, то в каждом из множеств содержится одно и то же число векторов.

Доказательство. Если в одном множестве m векторов, а в другом k векторов, то по теореме 2 и , т.е. .

В любом пространстве число линейно независимых векторов, порождающих пространство, называется размерностью пространства. Совокупность k линейно независимых векторов, порождающих k-мерное пространство, называется базисом пространства. Любая совокупность из более чем k векторов из k-мерного пространства, линейно зависима. Из теоремы 1 следует, что не существует совокупности менее чем из k векторов, порождающей k-мерное пространство.

Теорема 4. Если V есть k-мерное векторное пространство, то любая совокупность из k линейно независимых векторов, принадлежащих V, является базисом.

Пример:

Базисы 3-мерного пространства {000, 001, 010, 011, 100, 101, 110, 111} есть три множества по три линейно независимых вектора:

, , .

Теорема 5. Если векторное пространство V₁ содержится в векторном пространстве V₂ и оба пространства имеют одну и ту же размерность k, то эти пространства совпадают.

Скалярным произведением двух последовательностей длины n называется скаляр, определяемый как:

.

Если скалярное произведение двух векторов равно нулю, то говорят, что эти векторы ортогональны.