22. Кранмен қармап жүкті көтеру

Бұл жағдайда кран конструкциясының қаттылығын ғана ескереді К_к , яғни кран массасын m_k және жүк массасын m_г тек бір масса ретінде қарастырады. (1 сурет, b).

1- сурет. Жүктi қармап көтеруде динамикалық жүктеудiң сұлбасы: а - жебелі кран; б - көпірлік кран типтес; в - бiр массалы жүйенiң есептік схемасы; г - екi массалы жүйенің есептік схемасы.

Лагранждың қағидасын қолдана отырып, қозғалыстың теңдеуiн аламыз

Шешімі –

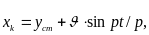
Мұндағы: статикалық жүктемеден конструкцияның иiлiмi; жүкті көтеру жылдамдығы; 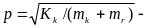еркiн тербелiстердi айналу жиiлiгі.

sin pt= -1 болғанда максимал динамикалық күшi

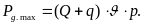
23. Автомобильдің вертикальды тербелісінің дифференциалдық теңдеуі

Автокөліктің рессорланған массасының серпімділік центрінің бос вертикаль тербелісінің дифференциалды теңдеуі (тербеліс жүйесінде кедергі болмағанда):

md²z/dt² + (C₁+C₂)z = 0

мұндағы m –автокөліктің рессорланған бөлігінің массасы; d²z/dt² –серпімділік центрінің үдеуі; C₁ + C₂ –алдыңғы және артқы аспалардың қосынды келтірілген қатаңдық коэффициенті; z – вертикаль ығысу не жылжу.

24. Массаға әсер ететін момент теңдеуі

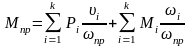
М_пр- келтiрiлген момент, - илік буынға әсер етуші күштің проекциясы, - илік буынға әсер етуші момент.

25. Күштерді және күштік моменттерді келтіру теңдеулері

Мұндағы және М_пр- келтiрiлген күш пен момент, - илік буынға әсер етуші күштің проекциясы, - илік буынға әсер етуші момент.

26.Автомобиль аспасы мен шинасының жалпы қаттылық коэффициенті

Аспа мен шинаның біріккен деформациясын ескеретін жалпы қатаңдық коэффициентін G жүгі әсерінен олардың қосынды иілу шартынан анықтауға болады:

f = f_п + f_ш = G/C_п + G/C_ш

мұндағы f_п –аспаның иілуі; f_ш –шинаның иілуі.

Осыдан жалпы қаттылық коэффициентін табамыз:

С = G/f = G/(G/C_п + G/ C_ш) = C_п C_ш/( C_п + C_ш).

27. Драглайн қозғалысын Лагранж тәсілімен анықтау

Лагранж әдісін драглайн шөмішін кенеттен босату жағдайына қолданамыз, 1 суреттегі сұлбаға сәйкес келетіндей.

Кенеттен босатудан кейінгі, арқанның келтірілген массасын ескергендегі шөміштің кинематикалық энергиясы:

.

Потенциалдық энергия арқан ұзындығы қысқарған кезде шөмішті көтергеннен пайда болады, сондай-ақ шөмішті босату кезінде, көтергіш арқанның деформациясының потенциалдық энергиясы азайған кезде де пайда болады.

Тапсырманы шешу үшін, шөміш тербелісінің жоғарыда келтірілген мәндерін қабылдаймыз.

Шөмішті биіктікке көтерген кезде, босату әсерінен потенциалдық энергия көбейеді:

.

Екінші жағынан, иілгіш дене ретінде арқанның бастапқы потенциалдық энергиясы мынаны құрайды:

;

Соңғысы .

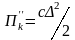Бұл жағдайларда бұл шамалардың айырмашылығын арқанның потенциалдық энергиясының азаюмен анықталады:

.

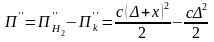Осылайша 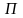потенциалдық энергияның толық өсуі мынадай болады:

(5)

Лагранж теңдігінің барлық мүшелерін анықтаймыз:

;

;

(6)

(6) формуладан және басқа да көптеген практикалық тапсырмалардан шығатыны, жүйенің кинетикалық энергиясы жалпыланған жылдамдыққа тәуелді және жалпыланған координаталарын өзгерткен кезде де өзгеріссіз қалады:

.

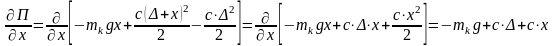Алынған формулаларды Лагранж теңдігіне қоя отырып, табатынымыз:

немесе .

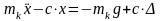Бірақ болғандықтан, ізделіп отырған бос шөміш қозғалысының теңдігі мынадай болады:

(7)

Даламбер принципі бойынша алынған (7) және (4) теңдіктер ұқсас.

Лагранж әдісімен құрылған (7) теңдік, бұл жағдайда әрекеттегі күштерді және инерция күштерініңқозғалыс бағытын талап етпейді. Осы себептен де үдеудің және инерция күшінің бағыты белгісіз болған кезде Лагранж әдісі қиын жүйелер үшін жақсырақ,осы себептен де жоғары да келтірілген Даламбер әдісі қолданылмауы керек.