2 Методические указания к выполнению ргр

Прежде чем выполнять то или иное задание, необходимо проработать теорию раздела, разобрать данный пример и только потом приступать к решению задачи.

2.1 Стягивающие деревья

Стягивающим (или остовным) деревом связного графа G называется произвольные его подграф G, содержащий все вершины графа G и являющийся деревом.

Существуют эффективные алгоритмы нахождения стягивающего дерева минимального веса в связном взвешенном графе.

В алгоритме Прима («ближайшего соседа») строится «разрастающееся» дерево, т.е. последовательность деревьев:

S₁ S₂ S₃…S_n,

где S_i=<V_i, E_i> содержит i вершин (i=1, 2, …, n).

Этапы алгоритма «ближайшего соседа»:

1. Отмечаем произвольную вершину графа, с которой начинаем построение. Строим ребро наименьшего веса, инцидентное этой вершине в остовном дереве Т.

2. Ищем ребро минимально веса, одной из двух полученных вершин. В множество поиска не входит полученное ребро, так как оно исключается из исходного графа.

3. Продолжаем далее, разыскивая каждый раз ребро наименьшего веса, инцидентное построенным вершинам, не включая в круг поиска все ребра, их соединяющие.

4. Процесс продолжаем до тех пор, пока все вершины исходного графа не будут включены в Т, которое и будет минимальным остовным деревом.

Замечание: если исходный граф является ориентированным, то при реализации алгоритма необходимо учитывать направление дуг.

Рассмотрим пример решения задачи, используя алгоритм Прима.

Пример. Для графа, изображенного на рисунке 2.1, с помощью алгоритма Прима найти стягивающее дерево минимального веса.

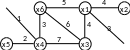
Рис. 2.1

Решать задачу будем пошагово, согласно алгоритму Прима.

Шаг 0. Выберем произвольную вершину, принадлежащую множеству вершин данного графа. Например, возьмем вершину х₁ и включим ее в остовное дерево Т.

Шаг 1. Вершинам, инцидентным вершине х₁ сопоставим пометки (a_i, b_i), где b_i – наименьший вес ребра, соединяющего вершину х_i c вершиной, уже включенной в дерево, т.е. на данном шаге вершиной х₁, а a_i – номер соответствующей вершины (х₁). Остальным вершинам, не инцидентным вершине х₁ присвоим пометку (0, ∞).

Полученные данные занесем в таблицу 2.1, первая строка которой соответствует шагу, вторая – множеству вершин V графа, не включенных в остовное дерево Т, следующие 5 строк для пометок вершин х₁, а в последних двух строках будем записывать наименьший вес min (b_i) и соответствующее ему ребро (a_i, х_i), вершину которого необходимо включить в дерево Т.

Вершине х₁ инцидентны вершины х₂, х₃ и х₆. Вершине х₂ сопоставим пометку равную (х₁, 4), так как х₁ – единственная вершина, включенная в остовное дерево и соединенная с вершиной х₂, а 4 – это вес ребра [х₁, х₂]. Аналогично находим пометки для других вершин графа. Для вершины х₃ пометка равна (х₁, 4), а для вершины х₆ - (х₁, 5). Получаем что наименьший вес имеют ребра [х₁, х₂] и [х₁, х₃], т.е. min (b_i)=b₂= b₃=4. Поэтому выбираем любое ребро, например [х₁, х₂], и добавляем его в стягивающее дерево Т (табл. *.1).

Шаг 2. Каждой вершине из множества V={х₃,…, х₆} сопоставляем пометку, состоящую из наименьшего веса ребра, соединяющего вершину с какой-либо вершиной из множества V_T={х₁, х₂}, и номера соответствующей вершины. Как видно из Таблицы *.1 на этом шаге в дерево Т добавилось ребро [х₂, х₃] с весом min (b_i)= b₃=3.

Шаги 3 – 5 выполняем аналогичным образом.

Таблица 2.1
шаг	1	2	3	4	5
Vгр	{х2,…, х6}	{х3,…, х6}	{х4, х5, х6}	{х4, х5}	{х4}
(a2, b2)	(х1, 4)	-	-	-	-
(a3, b3)	(х1, 4)	(х2, 3)	-	-	-
(a4, b4)	(0, ∞)	(0, ∞)	(х3, 7)	(х3, 7)	(х5, 2)
(a5, b5)	(0, ∞)	(0, ∞)	(0, ∞)	(х5, 1)	-
(a6, b6)	(х1, 5)	(х1, 5)	(х1, 5)	-	-
min (bi)	b2	b3	b6	b5	b4
новое ребро	х1 х2	x2 х3	х1 х6	x6 х5	х6 х5

В результате работы алгоритма получаем стягивающее дерево Т, изображенное на рисунке 2.2.

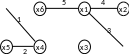
Рис. 2.2