
- •Дифференциальное исчисление функций многих переменных Занятие №1.
- •1. Определение функции
- •2. Предел и непрерывность функции
- •3. Частные производные
- •4. Дифференциал функции многих переменных
- •5. Задачи
- •6. Задания для самостоятельного решения
- •4. Градиент и производная по направлению
- •5. Задачи
- •6. Задания для самостоятельного решения
- •Занятие №3.
- •1. Экстремум функции многих переменных
- •2. Условный экстремум
- •3. Наибольшее и наименьшее значения функции многих переменных в замкнутой области
- •4. Задачи
- •5. Задания для самостоятельного решения
4. Градиент и производная по направлению
Если
каждой точке М некоторой области
пространства поставлено в соответствие
число (скаляр)
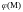 ,
то говорят, что задано скалярное поле.
,
то говорят, что задано скалярное поле.
Пусть
 −
единичный
вектор, задающий некоторое направление.
Производной от функции
по направлению
называется предел (если он существует)
−
единичный
вектор, задающий некоторое направление.
Производной от функции
по направлению
называется предел (если он существует)
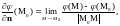
где
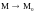 вдоль луча, выходящего из точки M0
по направлению вектора
,
вдоль луча, выходящего из точки M0
по направлению вектора
,
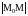 − длина
вектора
− длина
вектора
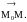 Пусть
Пусть
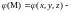 функция, непрерывно дифференцируемая
в точке M0,
функция, непрерывно дифференцируемая
в точке M0,
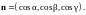
Тогда
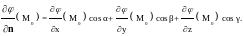
Градиентом скалярного поля φ называется вектор
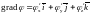 .
.
Заметим,
что
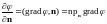 ,
и поэтому
,
и поэтому
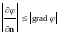 .Отсюда
следует, что направление
.Отсюда
следует, что направление
 характеризуется тем, что производная
в этом направлении будет наибольшей.
То есть
– вектор, направленный в сторону
наибольшего возрастания функции φ.
характеризуется тем, что производная
в этом направлении будет наибольшей.
То есть
– вектор, направленный в сторону
наибольшего возрастания функции φ.
5. Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения и понятия.
Записать уравнение касательной плоскости и нормали к поверхности
 в точке
в точке
 .
.
Ответ.
 ,
,
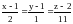 .
.
Найти градиент функции
 и ее производную в точке
и ее производную в точке
 в направлении от точки М к точке
в направлении от точки М к точке
 .
.
Ответ.
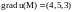 ,
,
 .
.
Найти
 ,
если
,
если
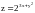 ,
,
 ,
,
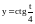 .
.
Найти
 ,
если
,
если
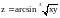 ,
,
 .
.Найти
 ,
,
 ,
если
,
если
 ,
,
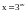 ,
,
 .
.Найти
 ,
если
,
если
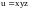 ,
,
 ,
,
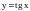 ,
,
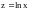 .
.Найти производную
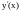 неявной функции, заданной уравнением
неявной функции, заданной уравнением
 .
.Найти
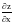 ,
,
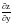 для неявной функции, заданной уравнением
для неявной функции, заданной уравнением
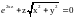 .
.
6. Задания для самостоятельного решения
Поверхность задана уравнением
 .
Записать уравнение касательной плоскости
и нормали к поверхности в точке
.
Записать уравнение касательной плоскости
и нормали к поверхности в точке
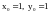 .
.
Ответ.
 ,
,
 .
.
Найти производную данной функции
 в точке
в точке
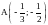 в направлении, составляющем угол
в направлении, составляющем угол
 с положительным направлением оси ОХ.
с положительным направлением оси ОХ.
Ответ.
 .
.
Найти градиент функции
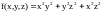 в точке
в точке
 ,
а также его длину и направляющие
косинусы.
,
а также его длину и направляющие
косинусы.
Ответ.
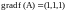 ,
,
 ,
,
 .
.
Найти , если
 ,
,
 ,
,
 .
.
Ответ.
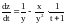 .
.
Найти
 ,
если
,
если ,
,
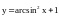 .
.
Ответ.
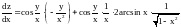 .
.
Найти , если
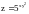 ,
,
 .
.
Ответ.
 .
.
Найти , , если
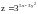 ,
,
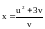 ,
,
 .
.
Ответ.
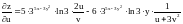 ;
;
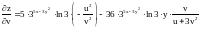 .
.
Найти
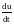 ,
если
,
если
 ,
,
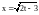 ,
,
 ,
,
 .
.
Ответ.
 .
.
Найти
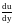 ,
если
,
если
 ,
,
 ,
,
 .
.
Ответ.
 .
.
Найти
 ,
если
,
если
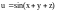 ,
,
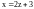 ,
,
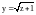 .
.
Ответ.
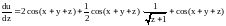 .
.
Найти производную
 неявной функции, заданной уравнением
неявной функции, заданной уравнением
 .
.
Ответ.
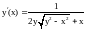 .
.
Найти , для неявной функции, определенной уравнением:
1)
 ;
2)
;
2)
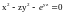 ;
3)
;
3)
 .
.
Ответ.
1)
 ,
,
 .
.
2)
 ,
,
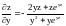 .
.
3)
 ,
,
 .
.
Занятие №3.
1. Экстремум функции многих переменных
Пусть
функция
 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки
 .
Говорят, что точка М является точкой
максимума (минимума) функции
,
если существует окрестность V точки М,
такая что для любой точки N из этой
окрестности V, отличной от точки М,
справедливо неравенство f(N) < f(M) (f(N) >
f(M)). Точки максимума и точки минимума
функции называют точками экстремума
функции, а значения функции в этих точках
– экстремумами функции.
.
Говорят, что точка М является точкой
максимума (минимума) функции
,
если существует окрестность V точки М,
такая что для любой точки N из этой
окрестности V, отличной от точки М,
справедливо неравенство f(N) < f(M) (f(N) >
f(M)). Точки максимума и точки минимума
функции называют точками экстремума
функции, а значения функции в этих точках
– экстремумами функции.
Теорема (необходимое условие экстремума). Если М – точка экстремума дифференцируемой функции , то
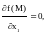
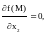 .
. .
.
. .
 .
.
Точка М, в которой выполнены эти условия, называется стационарной точкой. Не любая стационарная точка функции является точкой экстремума. Следующая теорема даёт достаточное условие для того, чтобы стационарная точка функции двух переменных была точкой экстремума.
Теорема
(достаточное условие экстремума для
функции двух переменных). Пусть
 – стационарная точка функции двух
переменных u = f(x; y), дважды непрерывно
дифференцируемой в некоторой окрестности
точки М.
– стационарная точка функции двух
переменных u = f(x; y), дважды непрерывно
дифференцируемой в некоторой окрестности
точки М.
Рассмотрим определитель
 .
.
1) Если
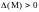 ,
то
является точкой экстремума функции
u(x; y) = f(x; y), а именно: а) если
,
то
является точкой экстремума функции
u(x; y) = f(x; y), а именно: а) если
 ,
то М – точка минимума; б) если
,
то М – точка минимума; б) если
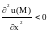 ,
то М – точка максимума.
,
то М – точка максимума.
2) Если
 ,
то М не является точкой экстремума.
,
то М не является точкой экстремума.
Теорема
(достаточное условие экстремума для
функции трёх переменных).
Пусть
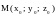 – стационарная точка функции
– стационарная точка функции
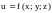 ,
дважды непрерывно дифференцируемой в
некоторой окрестности точки М. Рассмотрим
определители
,
дважды непрерывно дифференцируемой в
некоторой окрестности точки М. Рассмотрим
определители
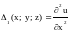 ,
,  ,
,
 .
.
Пусть
 .
Тогда имеем:
.
Тогда имеем:
a)
если
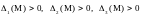 ,
то
– точка минимума;
,
то
– точка минимума;
б)
если
 ,
то
– точка максимума;
,
то
– точка максимума;
в) во всех остальных случаях (при условии ) М не является точкой экстремума.
