МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Технологический институт федерального государственного образовательного учреждения высшего профессионального образования «Южный федеральный университет» в г. Таганроге

Факультет автоматики и вычислительной техники

Кафедра Математического обеспечения и применения ЭВМ

Индивидуальное задание по

дискретной математике.

Вариант №28.

Выполнил:

студент группы А-91

Чепурной

Александр

Проверила:

доцент каф. МОП ЭВМ

Родзина Ольга Николаевна

Оценка ______________________

«____» __________ 2019 г.

Оглавление

Задание 1.

“Разумеется, хорошая математика всегда красива…” П. Д. Коэн.

ТЕОРЕТИЧЕСКАЯ ОСНОВА:

При доказательствах были использованы законы алгебры логики для простых и составных высказываний:

Также имели место следующие законы с константами:

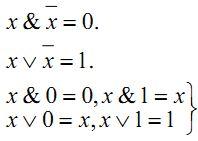
ПРАКТИЧЕСКАЯ ЧАСТЬ:

Доказать или опровергнуть всеми известными вам методами справедливость следующих равенств:

• Пример 1.

A\ (B\C) =? (A\B) ⋃ (A⋂B⋂C), т.е. M⊆N? и N⊆M?

1. Метод взаимного включения.

M⊆N?

∀x∈A & x∉(B\C) → x∈A & (x∉B ∨ x∈C) →конъюнкция с единицей → x∈A & (1 & (x∉B ∨ x∈C)) → x∈A & ((x∈B ∨ x∉B) & (x∉B ∨ x∈C)) → x∈A & (x∉B ∨ x∈B & x∈C) → x∈A & x∉B ∨ x∈A & x∈B & x∈C → x∈ (A\B) ⋃ x∈ (A⋂B⋂C) → x∈ ((A\B)⋃(A⋂B⋂C) → M⊆N → прямое включение доказано.

N⊆M?

∀x∈ (A \B) ⋃ x∈(A&B&C) → x∈A & x∉B ∨ x∈A & x∈B & x∈C → x∈A & (x∉B ∨ x∈B & x∈C) →x∈A & (x∈B ∨ x∉B & x∈C ∨ x∉B) →(x∈A & x∈C ) ∨ (x∈A & x∉B) → x∈A & x∉(B\C) → x∈ (A\(B\C)) → N⊆M → обратное включение доказано.

2. Путем эквивалентных преобразований.

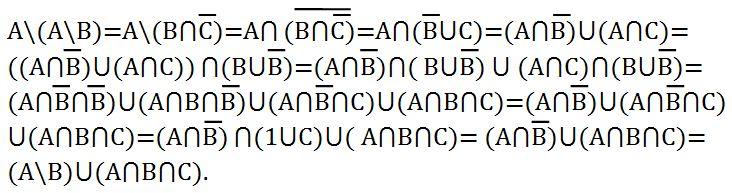
⇒доказали справедливость утверждения.

3. Доказательство от противного.

∃x∈(A\(B\C))\((A\B)⋃(A⋂B⋂C)) → x∈A\(B\C) & x∉(A\B)⋃(A⋂B⋂C) → x∈A & (x∉B v x∈C) & (x∉A v x∈B) & (x∉A v x∉B v x∉C) → (x∈A & x∉B v x∈A & x∈C) & (x∉A v x∈B) & (x∉A v x∉B v x∉C) → ((x∈A & x∉B & x∉A) v (x∈A & x∉B & x∈B) v (x∈A & x∈C & x∉A) v (x∈A & x∈C & x∈B)) & (x∉A v x∉B v x∉C) → (x∈A & x∈C & x∈B) & (x∉A v x∉B v x∉C) → (x∈A & x∈C & x∈B & x∉A) v (x∈A & x∈C & x∈B & x∉B) v (x∈A & x∈C & x∈B & x∉C) → 0 v 0 v 0 → ∅ → что и требовалось доказать.

4. Используя диаграммы Эйлера — Венна.

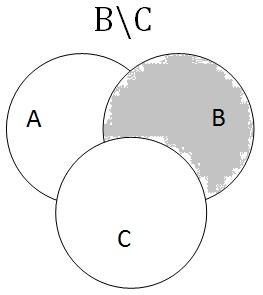
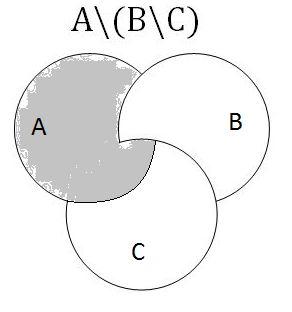
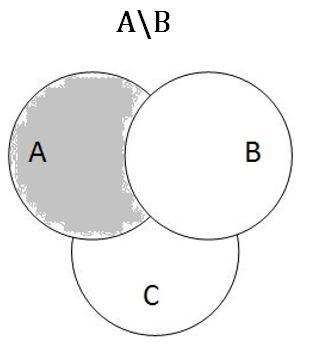
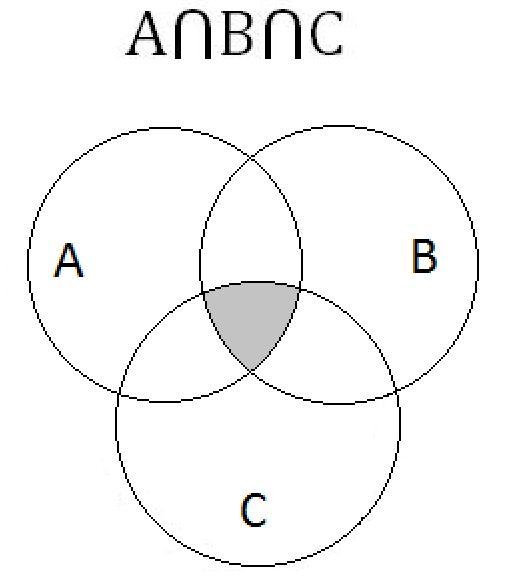
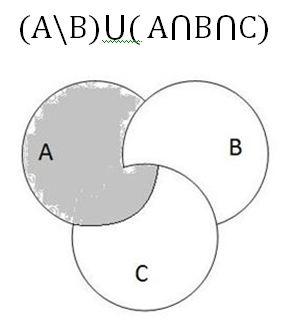
⇒Из диаграмм видно, что мы имеем дело с эквивалентными множествами. Выполнив строго определенную последовательность действий, имеем одинаковые результаты, следовательно, равенство выражений доказано.

• Пример 2.

(A\(B\C))\((A\B)⋃(A⋂C)=?∅.

Доказательство:

∃x∈(A\(B\C))\((A\B)⋃(A⋂C) → x∈ A\(B\C) & x∉ A\B & x∉ A⋂C → x∈A & (x∉B v x∈C) & (x∉A v x∈B) & (x∉A v x∉C) → ((x∈A & x∉B) v (x∈A & x∈C)) & ((x∉A & x∉A) v (x∉A & x∉C) v (x∈B & x∉A) v (x∈B & x∉C) → (x∈A & x∉B & x∉A) v (x∈A & x∉B & x∉A & x∉C) v (x∈A & x∉B & x∈B & x∉A) v (x∈A & x∉B & x∈B & x∉C) v (x∈A & x∈C & x∉A) v (x∈A & x∈C & x∉A & x∉C) v (x∈A & x∈C & x∈B & x∉A) v (x∈A & x∈C & x∈B & x∉C) → 0v0v0v0v0v0v0v0 →∅, что и требовалось доказать.

*Для доказательства были использованы те же самые законы, что и в прошлом примере*

Задание 2.

ТЕОРЕТИЧЕСКАЯ ОСНОВА:

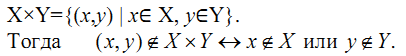
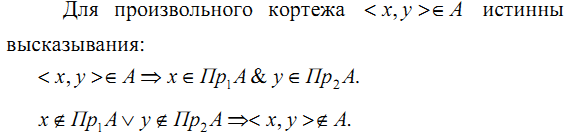
ПРАКТИЧЕСКАЯ ЧАСТЬ:

• Пример 1.

Доказательство от противного:

∃<x,y>∈X*(Y⋃Z) & <x,y>∉(X*Y)⋃(X*Z) → x∈X & y∈Y⋃Z & <x,y>∉X*Y & <x,y>∉X*Z → ((x∈X & y∈Y) v (x∈X & y∈Z)) & (x∉X v y∉ Y) & (x∉X v y∉Z) → x∈X & (x∈X v y∈Z) & (y∈Y v x∈X) & (y∈Y & y∈Z) & (x∉X v (y∉Y & x∉X) v (y∉Y & y∉Z)) → (x∈X ) & (y∈Y v (x∈X & y∈Z) & (x∉X v (y∉Y & y∉Z)) → (y∈Y v y∈Z) & x∈X & (x∉X v y∉Y) & (x∉X v y∉Z) → y∉Y & (y∈Y v y∈Z) & x∈X & (x∉X v y∉Z) → (y∉Y & y∈Z) & (x∈X & y∉Z) → ∅, верно, т.е. утверждение доказано.

• Пример 2.

Метод взаимного включения:

1. Прямое включение, т.е. M⊆N?

∀(x,y) ∈ X*(Y\Z) →x∈X & y∈Y\Z → x∈X & y∈Y & y∉Z→ объединяем с нулем → x∈X & y∈Y & y∉Z v x∈X & x∉X & y∈Y → x∈X & y∈Y & (x∉X v y∉Z) → (x,y) ∈ X*Y & (x,y) ∉ X*Z → <x,y> ∈(X*Y)\(X*Z) → M⊆N.

2. Обратное включение, т.е. N⊆M?

∀(x,y) ∈(X*Y)\(X*Z) → x∈ X*Y & x∉ X*Z → x∈X & y∈Y &(x∉X v y∉Z ) → x∈X & y∈Y & x∉X v x∈X & y∈Y & y∉Z → x∈X & y∈(Y\Z) → (x,y) ∈ X*(Y\Z) → N⊆M.

Прямое и обратное включения доказаны, следовательно, X*(Y\Z) = (X*Y)\(X*Z). Первоначальное утверждение неверно.