3.Задача линейного программирования

Задача линейного программирования в общем виде содержит три основных элемента модели:

- управляемые переменные;

- целевую функцию;

- ограничения на значения управляемых переменных.

При этом ограничения имеют вид неравенств или уравнений, связывающих управляемые переменные. В эти ограничения и целевую функцию управляемые переменные входят линейным образом.

Задача заключается в том, чтобы подобрать такие неотрицательные значения управляемых переменных, при которых целевая функция принимает наименьшее или наибольшее значение, причем выполняются все ограничения.

Таким образом, в общем виде задача формулируется следующим образом:

Найти неотрицательные значения переменных x₁, … , x_n, при которых целевая функция

f = a₁x₁+ … + a_nx_n  max (min),

причем выполняются ограничения вида

b₁x₁+ … + b_nx_n = b;

c₁x₁+ … + c_nx_n ≥ c;

d₁x₁+ … + d_nx_n ≤ d.

Ограничения могут быть в любом количестве и иметь любой из приведенных видов или несколько видов. Впрочем, все ограничения можно привести к одному виду, а требование максимизации функции f заменить на требование минимизации противоположной функции –f, и наоборот.

Геометрический смысл задачи линейного программирования удобно проиллюстрировать для случая, когда имеются две управляемые переменные. Для удобства назовем их х и у.

Пусть одно из ограничений имеет вид 2x – y ≥ 1. Чтобы изобразить соответствующую область на координатной плоскости, преобразуем уравнение к виду y ≤ 2x – 1. Изображаем на рис.1 прямую y = 2x – 1; искомая область – это полуплоскость, расположенная ниже этой прямой. Для удобства снабжаем прямую «бахромой», расположенной с той стороны, где находится заданная область.

Изобразим аналогично области, задаваемые остальными ограничениями (для наглядности считаем, что все ограничения являются неравенствами). Пересечение всех полуплоскостей образует некоторый выпуклый многоугольник, возможно, неограниченный. Хотя, возможно, пересечение окажется пустым, тогда задача является некорректной и не имеет решения. Если пересечение непустое, то назовем его допустимым многоугольником. Любая точка допустимого многоугольника определяет пару значений (x; y), для которых выполняются все ограничения задачи, и можно определить значение целевой функции для этих значений.

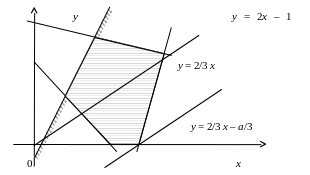
Рис.2

Рассмотрим теперь целевую функцию f. Для определенности возьмем f = 2x – 3y, и пусть f → max. Рассмотрим всевозможные прямые вида 2x – 3y = a, где а меняет свои значения. Например, при а = 0 имеем прямую 2x – 3y = 0, или y = 2/3 x. Для произвольного а прямая имеет уравнение y = 2/3 x – a/3. Все эти прямые параллельны друг другу. Можно сказать, что это одна прямая, двигающаяся параллельно самой себе с изменением а. В нашем случае при увеличении а прямая движется вниз.

Для любой точки прямой y = 2/3 x – a/3, пересекающей допустимый многоугольник, значение целевой функции f равно а. С увеличением а прямая опускается вниз. Если допустимый многоугольник ограничен, то в некоторый момент прямая дойдет до границы многоугольника. Соответствующей точке многоугольника и будет соответствовать максимальное значение целевой функции. Если же допустимый многоугольник неограничен, то возможно, что прямая все-таки достигнет его крайней точки, и задача будет иметь решение. Но возможно также, что прямую можно передвигать в соответствующем направлении неограниченно, и она все время будет пересекать допустимый многоугольник. В этом случае задача не будет иметь решения, так как целевую функцию можно увеличивать неограниченно.

Для решения задачи линейного программирования разработан симплекс-метод, заключающийся в построении специальных симплекс-таблиц. Но нет нужды разбирать его суть, так как созданы специальные компьютерные средства для решения этой задачи. Одно из этих средств разработано для программы EXCEL.