Ірраціональні, показникові, логарифмічні рівняння, нерівності, системи.

Зміст

Властивості степенів та арифметичних коренів. 1

Властивості логарифмів 2

Розділ І. Теоретичні відомості 2

1.1Ірраціональні рівняння 2

1.2 Системи ірраціональних рівнянь 6

1.3 Ірраціональні нерівності 7

1.4 Показникові рівняння 9

1.5. Показникові нерівності 12

1.6. Системи показникових рівнянь 12

1.7 Логарифмічні рівняння 13

1.8 Логарифмічні нерівності 16

1.9 Системи логарифмічних рівнянь 18

Розділ ІІ. Тестові завдання 19

Розділ ІІІ. Завдання з установленням відповідності. 26

Розділ ІV. Завдання з відкритою формою відповіді 32

Використані джерела 34

Властивості степенів та арифметичних коренів.

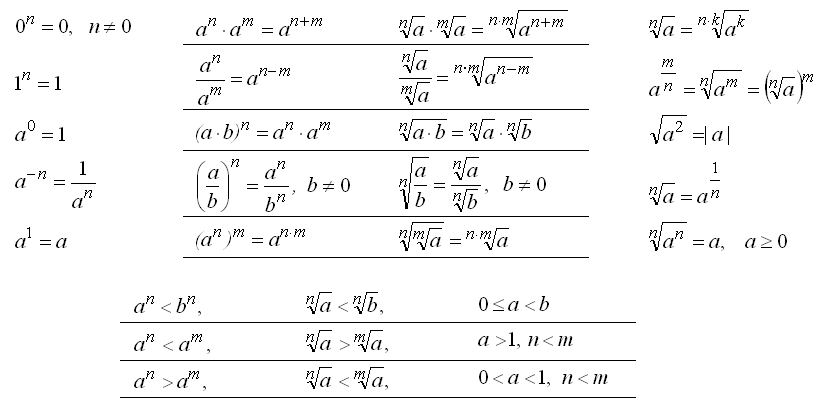
Властивості логарифмів

Розділ І. Теоретичні відомості

1.1Ірраціональні рівняння

Ірраціональними називаються рівняння, у якиx змінна міститься під знаком кореня (радикала) або під знаком піднесення до дробового степеня.

Наприклад:  - ірраціональні рівняння.

В окремих випадках, не розв’язуючи дане ірраціональне рівняння, можна встановити, що воно не має коренів. Наприклад, рівняння не має коренів, бо арифметичний корінь не може бути від’ємним.

Рівняння не має розв’язків, бо обидва доданки є арифметичними коренями, а тому не можуть бути від’ємними. А сума двох невід’ємних чисел дорівнює нулю лише тоді, коли кожен доданок дорівнює нулю. Одночасно ж вирази і нулю дорівнювати не можуть.

Основними методами розв’язування ірраціональних рівнянь є метод піднесення обох частин рівняння до одного і того самого степеня та метод введення нових змінних.

При розв’язуванні ірраціональних рівнянь методом піднесення обох частин до парного степеня можуть з’явитися побічні корені. Це відбувається за рахунок того, що при піднесенні обох частин початкового рівняння до парного степеня дістаємо рівняння, що є результатом не тільки рівняння , але і рівняння , оскільки і , і . Так, наприклад, візьмемо рівняння . Піднісши обидві частини цього рівняння до квадрата, дістанемо Коренями цього рівняння є числа Однак після перевірки переконуємось, що є коренем рівняння , а є побічним коренем.

Приступаючи до розв’язання ірраціонального рівняння, що містить парні степені радикалів, буває корисним знаходження області допустимих значень (ОДЗ), це, як правило, полегшує розв’язування рівняння. Якщо робити лише еквівалентні перетворення, то перевірку робити не потрібно. Розглянемо рівняння виду . Очевидно, що ліва частина рівняння, яка містить радикал парного степеня, не може бути від’ємна, а отже невід’ємна і права частина даного рівняння. Враховуючи область допустимих значень, підкореневий вираз також не може бути від’ємним. Отже, рівняння виду рівносильне такій системі:

Приклад 1. Розв’язати рівняння .

Розв’язання

Д ане рівняння можна звести до вигляду , тобто

.

З даної системи випливає, що лише є коренем початкового рівняння.

Відповідь: 2

Приклад 2. Розв’язати рівняння .

Розв’язання

Область визначення даного рівняння визначається в результаті розв’язання системи нерівностей

Перетворимо дане рівняння:

Обидва знайдені корені належать ОДЗ.

Відповідь: _.

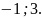
Приклад 3.Розв’язати рівняння .

Розв’язання

Знайдемо для початку область допустимих значень:

.

Оскільки область допустимих значень виявилась пустою множиною, то і розв’язків дане рівняння не має.

Відповідь: .

Таким чином, в даному прикладі попереднє знаходження ОДЗ виявилось надзвичайно корисним.

Приклад 4. Розв’язати рівняння .

Розв’язання

Знайдемо ОДЗ даного рівняння:

Піднесемо обидві частини рівняння до квадрата: . (1)

Останнє рівняння мало б місце при тобто при , але, враховуючи ОДЗ, , маємо, що

При перевірці дізнаємось, що є розв’язком рівняння (1). Оскільки рівняння (1) не має інших розв’язків, то і наше початкове рівняння має лише один розв’язок .

Відповідь: -1.