Контрольні запитання

1. Дайте означення електромагнітного поля.

2. Що називають електромагнітною хвилею?

3. Опишіть шкалу електромагнітних хвиль.

4. Сформулюйте та запишіть рівняння Максвелла.

5. Запишіть формули зв’язків між змінними величинами рівнянь Максвелла.

6. Запишіть формулу для швидкості поширення електромагнітних хвиль у середовищі.

7. Чому дорівнює фундаментальна швидкість?

8. Що таке площина поляризації?

9. Запишіть закон Бугера-Ламберта.

10. Дайте означення діаграми скерованості антени.

Лабораторна робота №46 Дослідження перехідних процесів в електричному контурі

МЕТА РОБОТИ:	вивчити властивості вільних коливань у замкнутому електричному контурі.
ОБЛАДНАННЯ:	електричний коливальний контур, осцилограф, джерело живлення, перемикач.

Теоретичні відомості

1. Контур Томсона

В електричних колах часто відбуваються вмикання чи від’єднання джерел живлення, короткі замикання ділянок кола, обриви віток тощо. У більшості випадків такі зміни в колі (комутації) проходять миттєво порівняно з тривалістю перехідних процесів.

Розглянемо процес розряду конденсатора ємністю через послідовно з’єднані котушку індуктивності та резистор з опором (контур В. Томсона), як наведено на рис. 1. Враховуючи, що напруга на індуктивності пропорційна швидкості зміни струмі в ній:

, (1)

напруга на ємності:

, (2)

а напруга на резисторі:

, (3)

за II правилом Кірхгофа запишемо диференційне рівняння для такого кола:

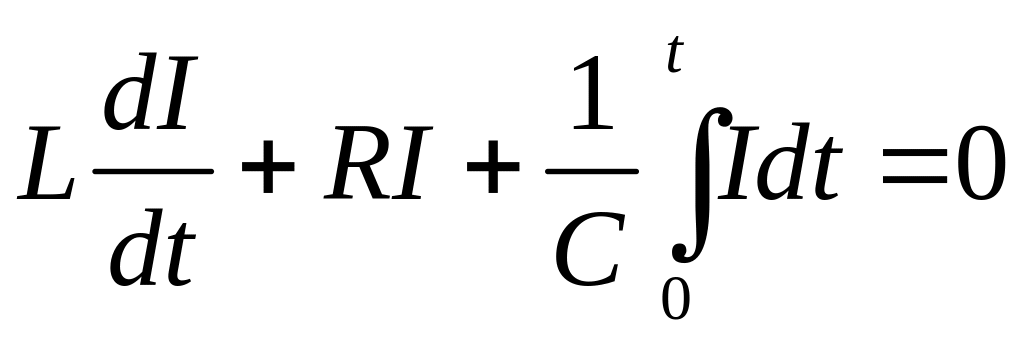. (4)

Після диференціювання за часом рівняння (4) набуде вигляду:

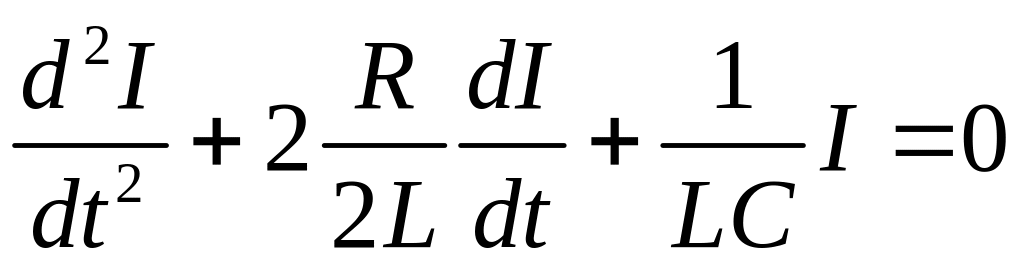. (5)

Увівши позначення для коефіцієнта згасання:

, (6)

а також для циклічної частоти власних коливань:

, (7)

отримаємо рівняння згасаючих коливань у канонічній формі:

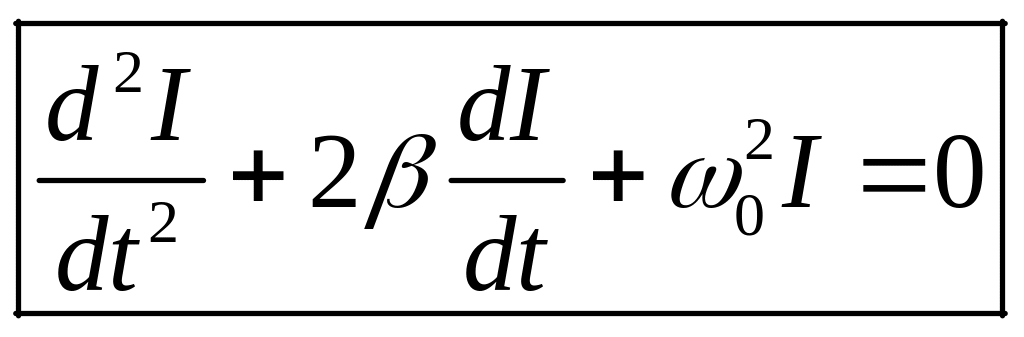. (8)

Враховуючи зв’язок між циклічною частотою та періодом коливань, за допомогою (8) отримуємо формулу Томсона:

. (9)

Розв’язком диференційного рівняння (8) буде функція від часу :

, (10)

де:

(11)

– частота вільних коливань, а – їх початкова фаза.

Зважаючи, що в початковий момент часу , а = , отримаємо вирази для неозначених коефіцієнтів у рівнянні (10):

; , (12)

тому остаточно вираз (10) набуде вигляду:

. (13)

Аналіз функції (11) показує, що при частота вільних коливань буде уявною, тобто коливання в контурі Томсона відсутні (процес буде аперіодичним). При говорять про критичний опір системи:

. (14)

П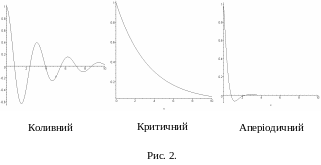 ри критичному опорі найшвидше згасають перехідні процеси (див. рис. 2).

2. Декремент згасання

Із виразу (13) видно, що амплітуда коливань зменшується з часом за експонентою:

. (15)

Відношення двох послідовних (які відрізняються на період коливань) максимальних значень струму називають декрементом згасання:

. (16)

Логарифм цього відношення буде логарифмічним декрементом згасання:

. (17)

На практиці зручніше користуватись не коефіцієнтом згасання, а добротністю контуру. Добротністю коливної системи називають величину, обернену до логарифмічного декремента згасання:

. (18)

При добротності , вільні коливання в системі не виникають.