
- •© Д.А. Захарчук, ю.В. Коваль, 2015
- •Передмова Основні вимоги до підготовки, виконання лабораторних робіт та оформлення звітів
- •Після виконання лабораторної роботи студент повинен:
- •При оформленні звіту студенту необхідно:
- •Для захисту лабораторної роботи студенту потрібно:
- •Похибки прямих та непрямих вимірювань в лабораторних роботах
- •1. Похибки прямих вимірювань
- •1.1. Абсолютні та відносні похибки
- •1.2. Обчислення похибки при непрямих вимірюваннях величин
- •Покажемо підхід Гауса на прикладі функції:
- •Лабораторна робота №51 визначення показника заломлення скла за допомогою мікроскопа
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №52 визначення довжини світлової хвилі за допомогою біпризми
- •Теоретичні відомості
- •Отже, в формулі (4) - це віддаль від щілини до біпризми, - це віддаль від щілини до об’єкта мікроскопа. Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №53 визначення радіуса кривизни лінзи за допомогою кілець ньютона
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №54 визначення довжини світлової хвилі за допомогою дифракційної ґратки
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №55 визначення концентрації розчину цукру за допомогою сахариметра
- •Теоретичні відомості
- •Опис установки
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота № 56 визначення температури за допомогою пірометра
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Лабораторна робота №57 Вивчення законів теплового випромінювання
- •Теоретичні відомості
- •Порядок виконання роботи
- •Контрольні запитання
- •Довідкові таблиці Префікси до одиниць вимірювання
- •Основні фізичні константи
- •Допоміжна література
- •43018 М. Луцьк, вул. Львівська, 75
Покажемо підхід Гауса на прикладі функції:
![]() . (2.2)
. (2.2)
Лінеаризуючи
![]() в
околі значень
в
околі значень
![]() отримаємо вираз для обчислення повного
диференціала:
отримаємо вираз для обчислення повного
диференціала:
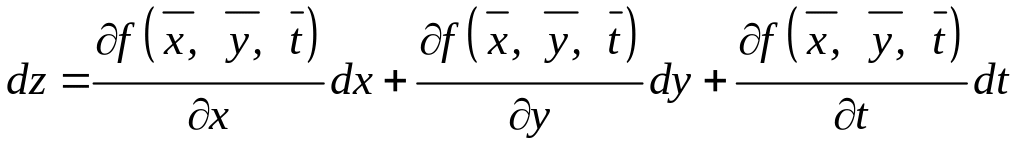
![]() (2.3)
(2.3)
Значення часткових похідних, взятих по модулю,
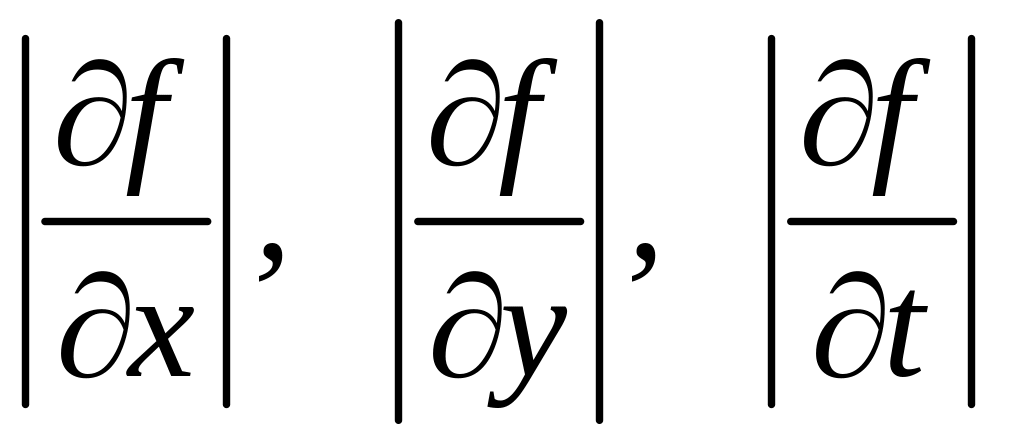 (2.4)
(2.4)
в
теорії похибок називають чутливостями
функції
відповідно до змін величин
![]() .
.
Для визначення абсолютної похибки непрямого вимірювання користуються формулою:
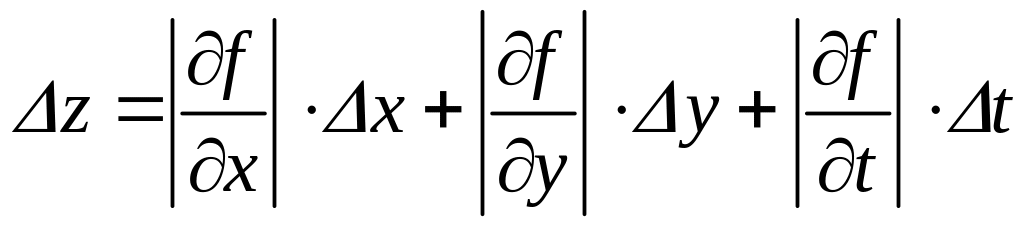 (2.5)
(2.5)
тобто, похибку непрямого вимірювання шукають згідно з тими ж правилами, що й повний диференціал цієї величини. Формальна відмінність полягає в тому, що всі арифметичні знаки ± при чутливостях змінюються на знаки +, а знаки диференціалів d – на значки похибок Δ.
Наведемо формули для обчислення абсолютних і відносних похибок:
суми:
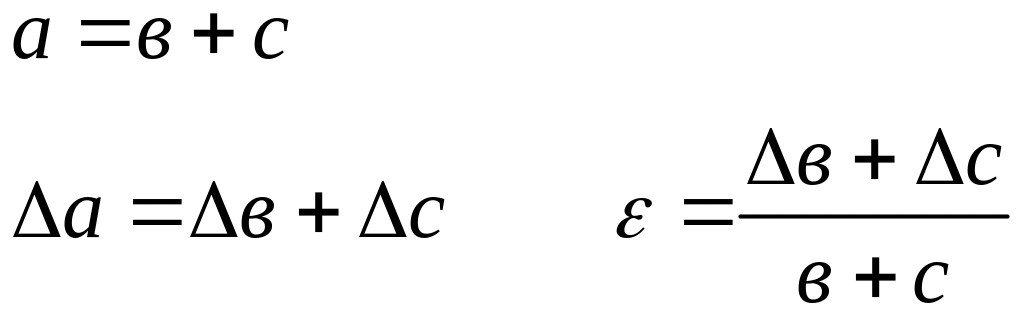 , (2.6)
, (2.6)
різниці:
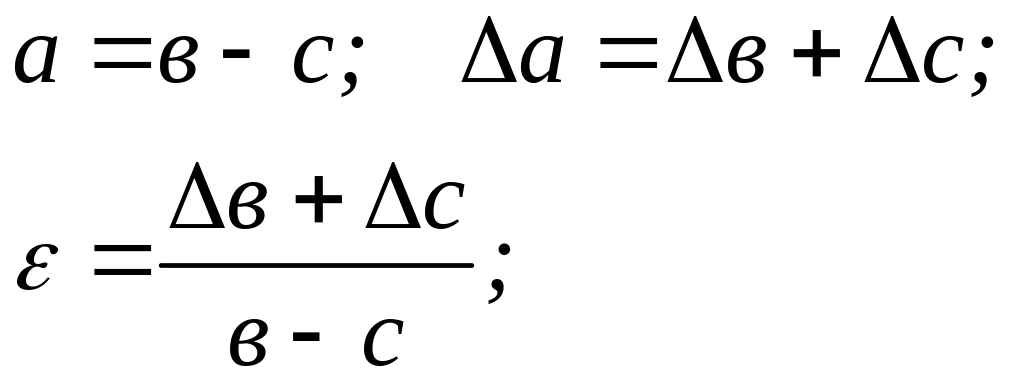 (2.7)
(2.7)
добутку:
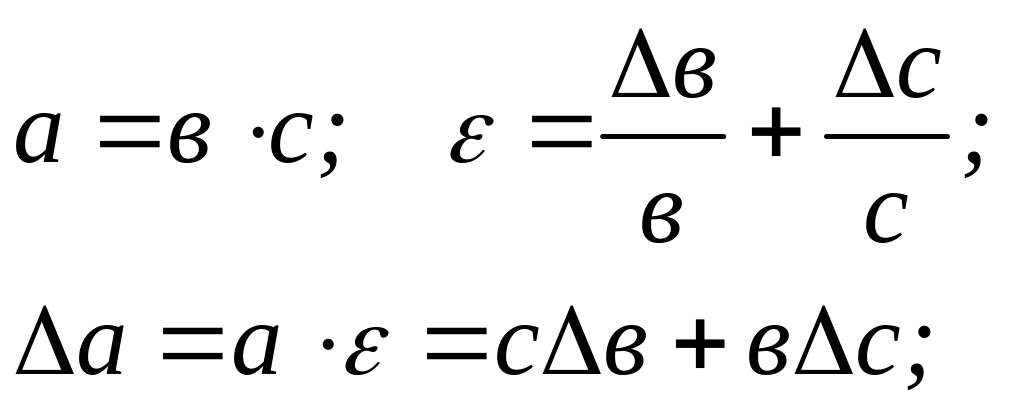 (2.8)
(2.8)
степеня:
![]() ; (2.9)
; (2.9)
дробу:
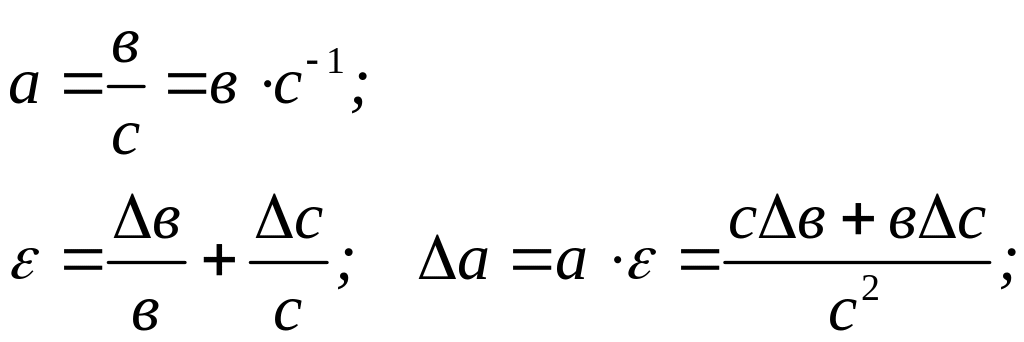 (3.0)
(3.0)
кореня:
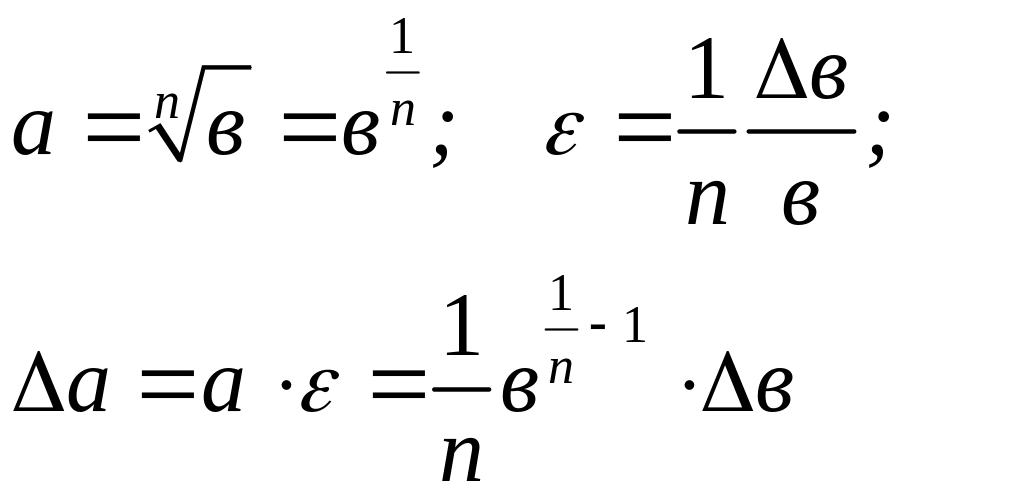 (3.1)
(3.1)
Якщо вираз для шуканої величини не містить значків ”+”чи “-“ (є термом), зручніше спочатку знаходити відносну похибку відповідно до правила: відносна похибка результату дорівнює сумі відносних похибок окремих змінних, взятих із такими коефіцієнтами, в якому степені вони входять у терм.
Наприклад, якщо шукана величина задана виразом:
![]() ,
,
то відносна похибка визначатиметься співвідношенням:
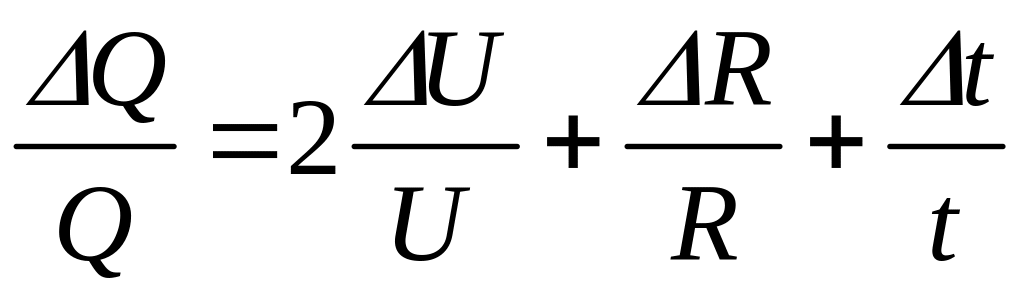 .
.
Лабораторна робота №51 визначення показника заломлення скла за допомогою мікроскопа
МЕТА РОБОТИ: |
визначити показник заломлення скла. |
ОБЛАДНАННЯ: |
вимірювальний мікроскоп з мікрометричним гвинтом, мікрометр, скляні пластинки з штрихами на обох поверхнях, освітлювач. |
Теоретичні відомості
За хвильовою теорією світло являє собою електромагнітні хвилі. Плоска електромагнітна хвиля, яка поширюється вздовж осі ОХ, описується рівняннями :
![]() , (1)
, (1)
![]() , (2)
, (2)
де:
![]() і
і
![]() – вектори наружності електричного і
магнітного полів; ω –
кругова частота;
– вектори наружності електричного і
магнітного полів; ω –
кругова частота;
![]() - хвильовий вектор.
- хвильовий вектор.
Досвід показує, що фізіологічна, фотохімічна та фотоелектрична дія світла викликається, в основному, коливаннями вектора , який називають світловим вектором. Фазова швидкість поширення електромагнітних хвиль:
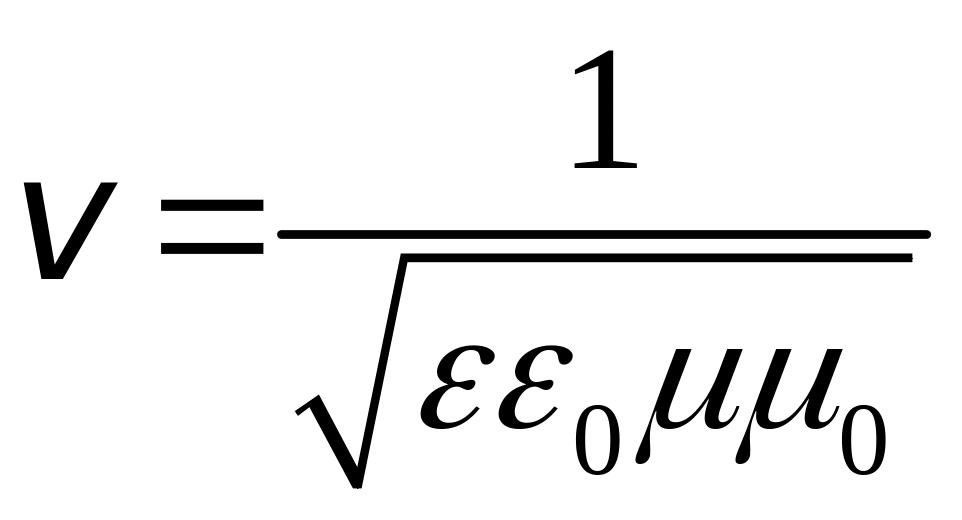 , (3)
, (3)
де: ε0 і μ0 – діелектрична і магнітна сталі для вакууму, ε і μ - діелектрична і магнітна сталі середовища.
Швидкість поширення світла в вакуумі:
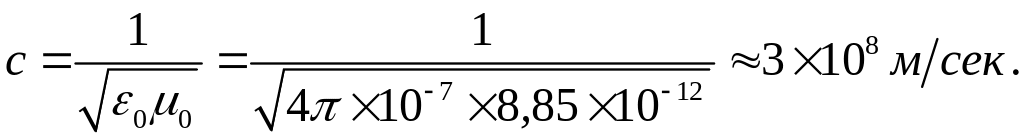 (4)
(4)
В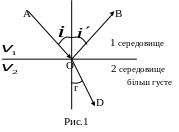 середовищі фазова швидкість світла
менша, ніж у вакуумі:
середовищі фазова швидкість світла
менша, ніж у вакуумі:
 , (5)
, (5)
де
![]() (оскільки для прозорих середовищ μ=1) –
показник заломлення даного середовища.
(оскільки для прозорих середовищ μ=1) –
показник заломлення даного середовища.
При проходженні світла через плоску границю двох прозорих середовищ неоднакової оптичної густини падаючий промінь АО розділяється на відбитий промінь ОВ і заломлений промінь OD (рис.1). При цьому:
![]() - закон
відбивання; (6),
- закон
відбивання; (6),
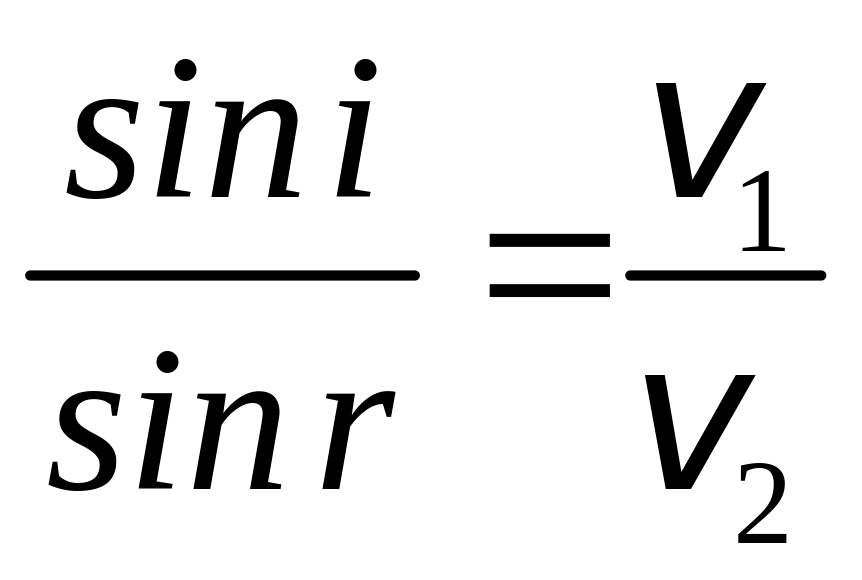 - закон
заломлення. (7)
- закон
заломлення. (7)
З закону заломлення (7) слідує, що відношення швидкості світла в середовищі 1 до швидкості в середовищі 2 є величина стала, тобто:
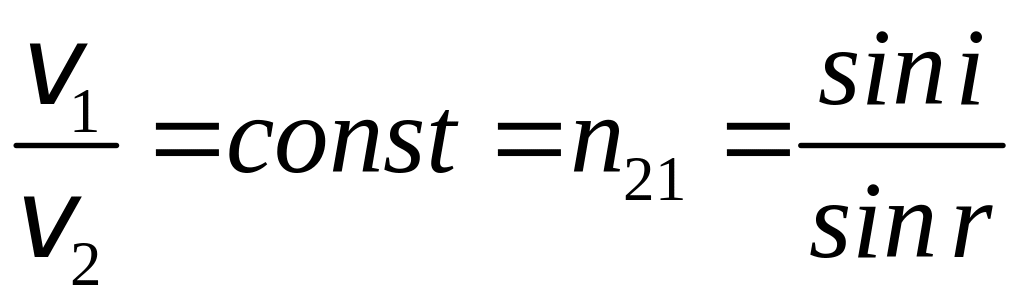 . (8)
. (8)
Величина n21 називається відносним показником заломлення другого середовища відносно першого. Якщо одне з середовищ, наприклад 1, - вакуум , то показник заломлення називається абсолютним. Отже, тоді:
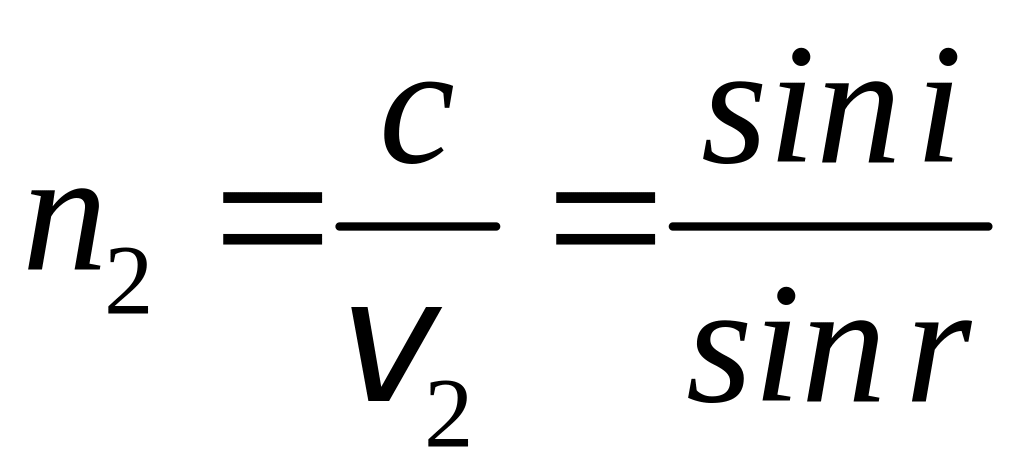 . (9)
. (9)
В
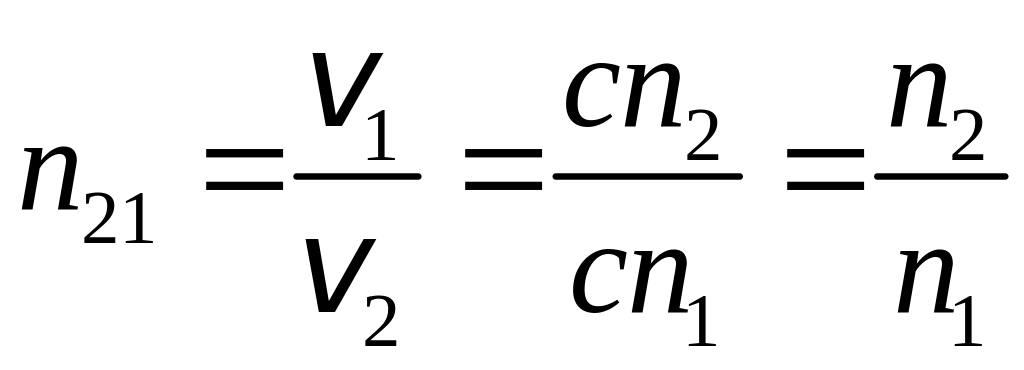 . (10)
. (10)
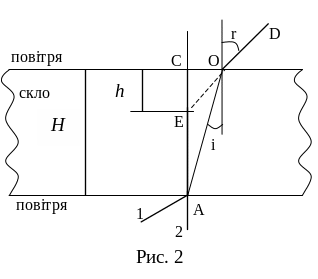
Одним з методів експериментального визначення показника заломлення скла є метод за допомогою мікроскопа. Схема проходження променів через скляну пластинку дана на рис. 2. В точку А падає два промені 1 і 2. Промінь 2 падає нормально і, не заломлюючись, виходить в точці С. Промінь 1 заломлюється і виходить в напрямку до точки D. Якщо дивитись з точки D в напрямку DО, то спостерігач буде бачити точку перетину променів ОD і АС не в точці А, а в точці Е, тобто товщина пластинки буде здаватись меншою Н і рівною СЕ = h. Для променів, близьких до нормально падаючих, кути падіння і заломлення малі. В цьому випадку синуси можна замінити тангенсами і за законом заломлення (7), розглядаючи обернений хід променів від D до А, можна записати:
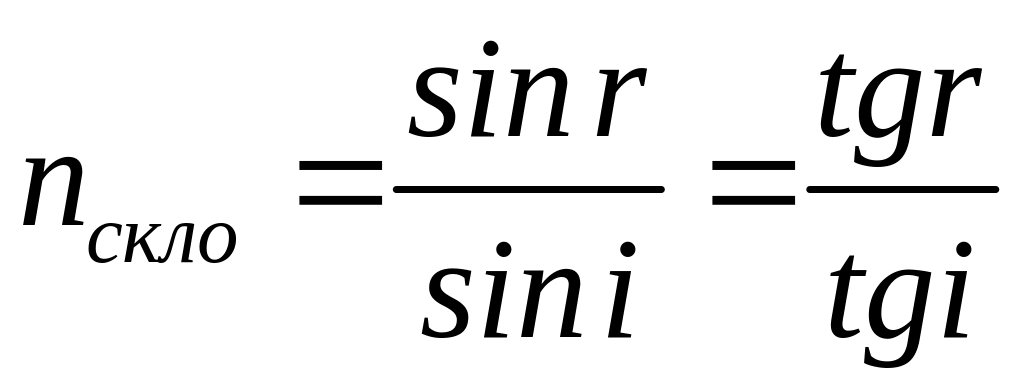 . (11)
. (11)
З рисунка маємо,
що
![]() .
Тобто:
.
Тобто:
![]() . (12)
. (12)
