
Дист лекции Кудряшов / Растворы
.pdf
Растворы неэлектролитов.
Растворами называются гомогенные системы, состоящие не менее чем из двух компонентов, состав которых может непрерывно меняться в широких пределах.
Растворы можно классифицировать с нескольких позиций:
1)По фазовому состоянию: твердые (например, сплавы), жидкие (морская вода, кровь) и газообразные (воздух).
2)По числу компонентов: бинарные, многокомпонентные.
3)По виду частиц, образующих раствор: растворы электролитов и растворы неэлектролитов. Растворы электролитов бывают бинарные (1соль+1растворитель) и смешанные (несколько солей+1растворитель; несколько растворителей + 1 соль). Растворы неэлектролитов это смеси взаимодействующих частиц: неполярные молекулы; простые жидкости; растворы сильно отличающихся по форме молекул (сферические и длинные).
4)Также по применяемой модели различают растворы идеальные, предельно разбавленные и реальные.
Стермодинамической точки зрения между растворителем и растворённым веществом нет разницы, все компоненты раствора равноценны. Однако на практике часто используют понятия растворитель и растворенные вещества. Обычно растворителем принято называть компонент, находящийся
визбытке. В случае жидких растворов растворителем называют компонент, который в чистом состоянии при рассматриваемых давлении и температуре, является жидкостью. А. Растворитель принято обозначать подстрочным индексом «1» или «А». Растворенные вещества обозначаются последующими цифрами и буквами «2,3,4,…» или «Б,В,Г,…».
Важнейшей характеристикой раствора является его состав, в который выражают как количество растворенного вещества, отнесенное к определенному количеству раствора или растворителя. В первом случае используют следующие виды выражения концентрации:
1.Массовая доля или массовый процент:
2.Мольная доля или мольный процент:
3.Объемная доля или объемный процент:
|
g |
i |
|
100 |
масс.% |
||
|
|
||||||
|
|
|
|||||
i |
gi |
|
|
||||
|
|
|
|
|
|
||
|
|
i |
|
|
|
|
|
Ni |
ni |
|
|
100 |
мольн.% |
||
ni |
|||||||
|
|
i |
|
|
|
|
|
i |
|
Vi |
|
100 |
объемн.% |
||
Vi |
|||||||
i

4. Молярность (иногда обозначается М)
|
|
n |
|
c |
i |
[ моль/ л] |
|
i |
|
V |
|
|
|
|
Во втором случае наиболее часто используют следующие виды выражения концентрации:
5. |
Моляльность (число молей (m) |
|
|
|
i |
|
|
|
|
|
|
|
mi |
|
n |
1000 |
[моль/1000г р-ля] |
||||
|
растворенного вещества, приходящегося |
|
A |
|||||||
|
|
g |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
на 1000 г растворителя): |
|
|
|
|
|
|
|
|
|
6. |
Масса вещества, приходящегося на 100 г |
|
i |
|
|
gi |
100 |
[г/100г р-ля] |
||
|
растворителя: |
|
|
g A |
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
где gi – масса растворенного вещества, Σgi – масса раствора, Vi – объем растворенного вещества, V – объем раствора, gА – масса растворителя.
Пересчет из одной концентрации в другую для разбавленных бинарных растворов можно осуществлять по следующим формулам:
с |
|
|
n |
|
|
|
n |
|
|
n |
|
|
n |
|
|
x |
|
||||
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
V |
|
g |
|
g |
|
n M |
|
n |
M |
|
n M |
|
|
M |
|
2 |
||
|
|
|
|
1 |
2 |
1 |
2 |
1 |
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
||||||
|
|
|
m |
|
|
n 1000 |
|
n 1000 |
|
|
1000 x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
g |
|
|
|
|
|
n M |
|
|
|
|
M |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
с |
|
|
n |
|
|
|
|
n |
|
|
n |
|
n |
|
1000 |
|
m |
|
|||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
V |
|
|
g |
|
g |
|
|
|
g |
|
|
|
g |
1000 |
|
|
|
1000 |
||||||||
|
|
|
|
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
N |
|
|
n |
2 |
|
|
|
m |
2 |
|
m |
2 |
M |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
n |
n |
|
|
1000 |
|
|
1000 |
|
1 |
|||
|
|
|
|
m |
|
|
|
|||||||
|
|
1 |
|
|
2 |
|
M |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для разбавленных водных растворов можно считать, что c2 ≈ m2, N2 ≈ 0,018m2. Следует отметить, что молем раствора называется такое его количество, когда число молей каждого компонента численно равно его мольной доле.
Парциальные мольные величины. Уравнения Гиббса-Дюгема
Термодинамические свойства, характеризующие состояние системы, как известно, подразделяются на экстенсивные и интенсивные. К экстенсивным свойствам относятся такие свойства которые зависят от размера (массы) системы: V, U, H, S, A, G. К интенсивным свойствам относятся свойства, не зависящие от размера системы: T,P, xi, μ. Обозначим через L - общее экстенсивное свойство системы.
Экспериментально было установлено, что, если смешать 5л воды и 5л спирта, то вновь образовавшийся объем будет несколько меньше 10л., т.е. общее интегральное свойство реального раствора, образовавшегося в результате смешения компонентов, не является аддитивным по отношению к чистым компонентам: n1 L10 +n2 L02 ; свойства отдельного компонента в

растворе и в чистом виде в общем случае не совпадают.
L0 i
- мольные
экстенсивное свойство i - того компонента.
Для определения общего интенсивного свойства вводится понятие парциальных мольных величин:
L f P,T , n |
, n |
2 |
... |
1 |
|
|
Например,
|
V |
V |
|
|
|
|
|
i |
|
|
n |
|
|
|
|
i |
P,T .n j i |
|
|
|
|
|||
|
|
|
|
|
|
L |
|
|
|
||
Li , |
||||||
|
|
|
||||
|
||||||
|
|
|
||||
|
ni P,T .n |
|
|
|
||
|
|
j i |
|
|
|
|
- парциальный мольный объем;
|
S |
|
S |
|
|
|
|
|
|
i |
|
|
n |
|
|
|
|
|
i |
P,T .n j i |
|
||
|
|
||||
|
|
|
|
|
|
-
парциальная мольная энтропия. Парциальная мольная величина i - того компонента отмечается верхней чертой в отличие от мольных величин, помечаемых подчеркивающей чертой снизу.
Парциальная мольная величина – представляет собой изменение общего экстенсивного свойства раствора при добавлении к нему 1 моля данного компонента при условии сохранения постоянства Гиббса-Дюгема и состава раствора. Очевидно, это возможно только, если берется бесконечно большое количество раствора.
Так как парциальные мольные величины отражают изменения свойств системы в целом, то они могут принимать значения, которые для мольных свойств чистых веществ являются абсурдными: например, парциальный мольный объем может быть отрицательным, равным нулю.
Так как экстенсивные величины являются функциями состояния, то
|
L |
|
|
|
dL |
|
|
|
dP |
|
|
|||
|
P T ,n ,n |
... |
||
|
1 |
2 |
|
|
|
L |
|
|
|
|
|
|
|
dT |
|
|
|||
|
T P,n ,n |
... |
||
|
1 |
2 |
|
|
|
L |
|
|
dn |
|
|
|
|
|
||
|
n |
|
|
1 |
|
|
P,T .n |
,n |
,... |
||
1 |
|||||
|
|
2 |
3 |
|
|
|
L |
|
dn |
|
|
... |
|
|
|
k |
||
|
|
n |
|
|
|
|
|
|
k |
P,T .n j k |
|
||
|
|
|
||||
|
|
|
|
|
|
|
при
или
P,T
|
|
|
k |
|
L |
|
|
|
|
|
|
, |
dL |
|
|
|
|
||||
const |
|
|
|
|
|
dni |
||||
|
n |
|
|
|
||||||
|
|
|
i 1 |
|
i |
P,T .n j i |
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
dL |
L dn |
L dn |
|
L dn |
|
|||||
|
1 |
1 |
2 |
2 |
|
|
|
i |
i |
|
L |
k |
dn |
|
k |
(1)
Парциальные мольные величины, характеризующие вклад одного моля i - того компонента в термодинамическое свойство раствора, зависят от состава раствора, но не зависят от его количества.
Интегрирование при условии сохранения состава раствора приводит к уравнению, которое называется первым уравнением Гиббса-Дюгема:
|
k |
|
L р ра |
|
Li ni |
|
i 1 |
|
Константа интегрирования здесь равна 0, т.к. при n = 0 L = 0. Для бинарного раствора:
L L1n1 L2 n2
для 1 моля бинарного раствора:
Lm L1x1 L2 x2
Если продифференцировать уравнение Гиббса-Дюгема при постоянных T,P,
|
k |
|
k |
|
то можно получить: dL |
|
Li dni |
ni dLi |
. Если заменить dL |
|
i 1 |
|
i 1 |
|
(1), то получим второе уравнение Гиббса-Дюгема:
по соотношению
k
i 1
n dL |
|
i |
i |
=0
Это уравнение записано для любого количества раствора, для моля раствора:
k
i 1
х dL |
|
i |
i |
.
Уравнения Гиббса-Дюгема показывают, что парциальные мольные величины не являются независимыми.
Если взять бинарный раствор, то для 1 моля такого раствора можно записать: x1dL1 x2 dL2 0 , отсюда можно получить:
|
|
|
|
L |
x |
|
|
x |
|
, |
|
|
|
|
|
|
1 |
|
2 |
|
2 |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
L |
2 |
x |
2 |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|||
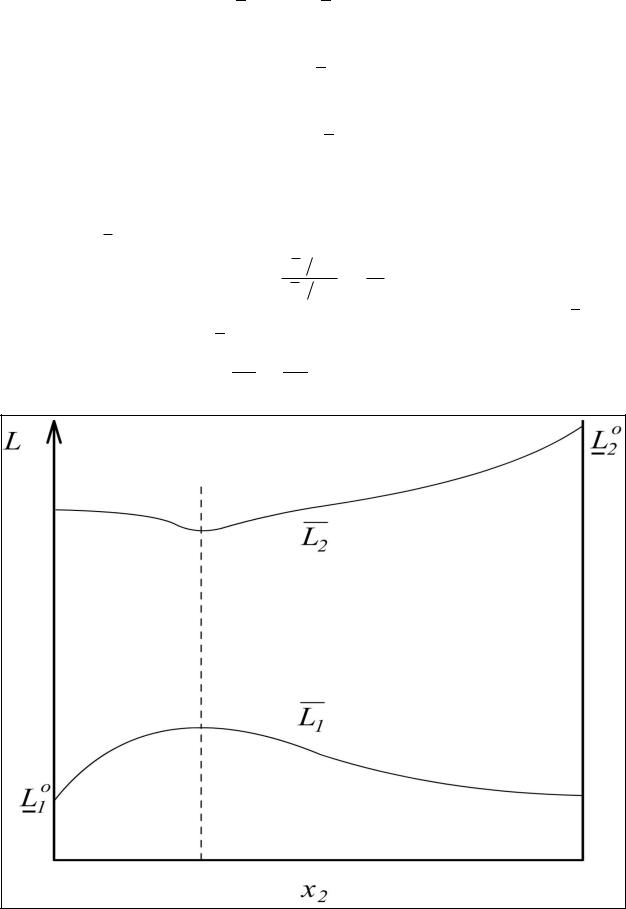
Т.е. производные имеют разные знаки. Если на одной кривой |
|||||||||||
имеется max, то на кривой L2 |
=f(x2) имеется min. |
|
|
||||||||
Если х1 х2 0,5 , то |
L |
|
L |
. |
|
|
|
|
|
||
|
1 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
x |
2 |
|
x |
2 |
|
|
|
|
|
|
L1
=f(x2)
m
Методы определения парциальных молярных величин
1.Аналитический метод. При вычислении этим методом выражают зависимость общего свойства от числа молейкомпонента эмпирическим уравнением. Например:
L A Bn |
2 |
|
Cn |
3 |
|
2 |
||
|
||
|
2 |
,
|
|
|
L |
|
3 |
|
|
|
|
|
|
|
|
|
|||
тогда |
|
|
|
|
1 |
, |
|
|
|
L L2 n2 |
|||||||
L |
|
|
|
|
B |
|
Cn |
2 |
L |
|
|
|
|||||
n |
|
2 |
n |
||||||||||||||
2 |
|
|
|
|
|
2 |
|
1 |
|||||||||
|
|
|
|
|
2 P,T ,n1 |
|
|
|
|
|
|
|
|
1 |
|
||
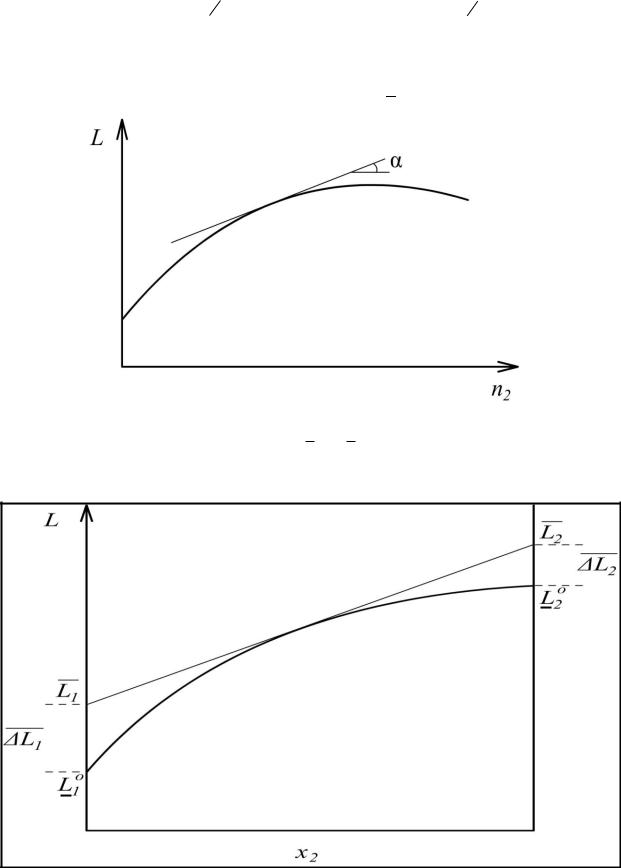
2.Графические методы а) метод касательных
зависимость L = f(n2) при
n1
const
,
L |
L / n |
|
2 |
2 |
P,T ,n |
|
|
j i |
tg
.
б) метод пересечений зависимость Lm f x
2
,
L |
1 |
|
и
L |
2 |
|
- отрезки на осях ординат.
m
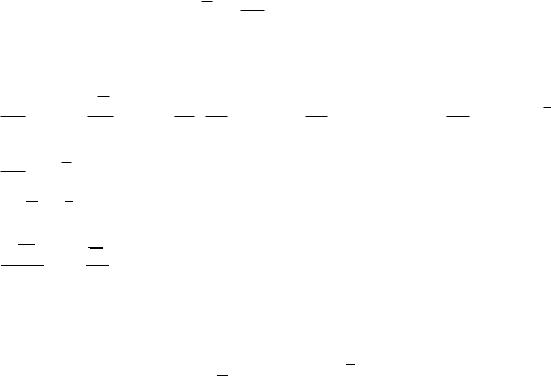
Химический потенциал компонента в растворе. Активность. Стандартные состояния.
Химический потенциал был определен как:
|
U |
|
|
H |
|
|
A |
|
|
G |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
n |
|
|
n |
|
|
n |
|
|
n |
|
||||
|
i S ,V ,n |
j i |
|
i S ,P ,n |
j i |
|
i T ,V ,n |
j i |
|
i P ,T ,n |
j i |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Только одно из этих соотношений подходит под определение парциальной мольной величины:
|
|
G |
|
|
G |
|
|
i |
i |
|
|
|
|
||
|
|
|
n |
|
|
||
|
|
|
|
|
i |
P,T ,n j i |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Из полученного соотношения, что химический потенциал зависит от Р,Т и состава раствора. Эти зависимости легко вспомнить по аналогии с G.
|
|
|
|
|
G |
|
|
|
i |
|
|
|
|
i |
|
T |
P,n |
|
|
T |
|
|
|
j i |
|
|
|
||||
|
|
|
|
|
|
|
|
|
i |
|
V |
|
|
|
|
||
|
|
|
|
|
P |
|
|
i |
|
T |
|
|||
|
|
|
|
|
|
i |
H |
i |
TS |
i |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
H i |
|||
|
|
T |
|
|
T |
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
G |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
P,n |
|
|
T |
ni |
P,T ,n |
|
ni |
T |
||||
j i |
|
|
|
|
|
j i |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
S |
|
||
|
|
|
|
|
|
|
|
n |
|
|
|
P,T ,n |
|
i |
|||
|
|||||
j i |
|
|
|
|
|
S |
i |
|
P,T ,n j i
Эти соотношения выражают зависимости химического потенциала от Р и Т.
Следует отметить, то если S 0 0 и V 0 0 всегда, то S может быть как больше
i i i
нуля, так и меньше, также как и парциальный мольный объем.
Зависимость химического потенциала μ от состава для компонента
идеальной газовой смеси мы уже определяли:
μi = μiст.+RTlnxi
Аналогичным соотношением определяется зависимость химического
потенциала компонента идеального раствора:
μi(ид.) = μiст.+RTlnxi
Для выражения этой же зависимости в реальных растворах используют,
предложенное Льюисом понятие активности компонента в растворе:
μi(реал.) = μiст.+RTlnаi.
Т.о. активность – это такая функция концентрации, которая будучи поставленной в уравнение для идеального раствора, делает его пригодным для реального. Активность также зависит от давления, температуры и
концентрации:
μi - μiст.=RTlnаi

ln a |
|
|
|
i |
|
|
|
|
|
T |
|
|
|
1 |
|
|
|
|
|
|
|
|
cт. |
|
||
|
|
|
|
|
|
|
|
i |
|
|
i |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
R |
T |
T |
|
|
T |
|||||||
P,x j |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
ln a |
|
|
|
|
|
V i |
V |
||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
T , x |
|
|
|
|
RT |
|||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
cт. |
|
H i H i |
||
|
RT |
2 |
|
|
|
|
|
cт. |
|
|
|
i |
. |
|
|
|
|
|
|
С концентрацией активность связана через коэффициент активности:
ai=xiγi
γi= ai/xi - рациональный коэффициент активности; γi= ai/сi - молярный коэффициент активности;
γi= ai/mi - моляльный коэффициент активности.
Разумеется, числовые значения коэффициента активности в каждом случае получаются разные.
Система стандартных состояний может быть симметричной и несимметричной. Если в качестве стандартных состояний выбираются чистые компоненты при температуре раствора, то в этом случае все компоненты являются как бы равноправными. Это симметричная система сравнения. В этом случае ai =1, при хi =1 и γi=1. Выражение для химического потенциала
μi = μiо+RTlnаi.
Активность в этом случае определяется как: ai=Pi/ Pio, где Pi – парциальное давление i – того компонента над раствором; Pio – давление насыщенного пара i – того компонента над чистым компонентом.
Если в качестве стандартного состояния для растворителя выбирают чистый компонент при температуре раствора, а для растворенного вещества выбирают гипотетический раствор, обладающий свойствами бесконечно разбавленного раствора, но имеющего единичную концентрацию, то в этом случае мы будем иметь несимметричную систему.
Для растворителя – стандартное состояние чистое вещество a1 =1, при
х1 =1 и γ1=1.
μ1 = μ1о(P,T)+RTlnx1 γ1.
Для растворенного вещества: m2 =1, γ2→1, a2→1
μ2 = μ2*+RTlnа2*.
Активность в этом случае для растворителя определяется как: a1=P1/ P1o, где P1 – парциальное давление растворителя над раствором; P1o – давление насыщенного пара над чистым растворителем, активность для растворенного вещества а2*=P2/ KГ, где P2 – парциальное давление растворенного вещества над раствором; KГ – константа Генри, о которой будет рассказано в следующей лекции.
Относительные парциальные молярные величины.
Относительная парциальная мольная величина определяется как:
Li Li Li,станд Li Li0 Примеры: Gi i Gi G i0 , Н i Н i H i0
Интегральные и дифференциальные теплоты растворения
а)
H
Дифференциальная теплота растворения |
H i |
H i |
H i |
|
|
|
0 |
- количество тепла, которое выделяется или поглощается при
|
растворении 1 моль i-того компонента |
в |
бесконечно большом |
|||||||||||||||
|
количестве раствора заданного состава |
|
|
|
|
|
|
|
||||||||||
|
Н |
|
Н |
|
(Н |
|
Н |
0 |
) |
H n H |
|
n |
|
1 |
|
0 |
||
кон |
исх |
Р,2 |
Р,1 |
2 |
2 |
2 |
(H n H n ) Н 2 |
|||||||||||
|
|
|
|
|
1 1 |
|
|
|
1 1 |
2 2 |
|
|||||||
Н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Интегральная теплота растворения – теплота, которая выделяется или поглощается, при растворении 1 моль данного компонента в таком количестве растворителя, которое обеспечивает образование раствора определенного (заданного) состава
Hинт H р р (n1H10 H 20 )
Свойства относительных п/м величин
|
|
|
H |
|
||||
а) математическое выражение |
H i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|||
|
|
|
i |
|
P,T ,n |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
j i |
б) соотношения между п/м свойствами: |
|
i |
H |
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
в) уравнения Гиббса-Дюгема для относительных
i
T S |
i |
и т.д. |
|
||
|
|
п/м величин
L L n |
|
|||
|
|
1 |
1 |
|
n d L |
n |
2 |
||
1 |
1 |
|
|
|
L2 d L2
n2 ,0
г) экспериментальное определение аналогично, например по зависимости Н инт
относительных п/м свойств
f х |
2 |
|
|
|
Функции смешения
Функции смешения - это изменение свойства при образовании растворов из молю образовавшегося раствора: LM
0 |
xi |
L1x1 |
LM Lкон Lисх L p ра Li |
соответствующего экстенсивного чистых веществ, отнесенное к 1
0 |
0 |
= |
L1x1 L2 x2 |
L2 x2 L1 x1 |
L2 x2 |
Все соотношения термодинамических свойств, полученных для обычных термодинамических свойств справедливы и для функций смешения:
G |
M |
|
G M H M TS M .
- всегда меньше 0, иначе не было бы раствора, он бы расслаивался.
H - эту величину можно измерить непосредственно в калориметре. |
M |
||
|
|||
M |
|
H |
|
|
|
|
|
может иметь любой знак. Чаще всего H |
M |
больше 0, например, хлороформ – |
|
|
|
|
|
ацетон. При образовании водородных связей знак может быть отрицательный. H M может быть и знакопеременной.
S |
M |
практически всегда положительна, она является ведущим слагаемым, |
|
||
|
|
хотя формально отрицательная энтропия смешения не противоречит законам термодинамики.
Изучение функций смешения позволяет группировать растворы по их свойствам.
