1.Для 8 значений X из диапазона 5..8 заполнить и распечатать массив y[I]
Построить график функции y(x).
Определить cр. арифметическое y[i]<2.
Определить cр. геометрическоеt abs(x[i])<6.
Определить максимальное значение y[i]<1
Определить минимальное значение x[i]>6
Программа
for i=1:8
x(i)=5+3*rand
if x(i)<=6
y(i)=cos(x(i));
else
y(i)=log(x(i));
end
end
[x' y']
plot(x,y,'*')
A=0;n=0;
for i=1:8
if y(i)<=2
A=A+y(i);
n=n+1;
end
end
A=A/n;
[A]
P=1;k=0;
for i=1:8
if x(i)>6
P=P*x(i);
k=k+1;
end
end
P=P^(1/k);
[P]
MaxY=-10;
for i=1:8
if (y(i)>MaxY)&(y(i)<1)
MaxY=y(i);
end
end
[MaxY]
MinX=10;
for i=1:8
if (x(i)<MinX)&(x(i)<6)
MinX=x(i);
end
end
[MinX]
Результат выполнения
x y
7.2119 1.9757
5.4096 0.6420
5.0353 0.3173
7.6817 2.0388
5.5974 0.7739
5.8962 0.9260
6.9843 1.9437
5.8532 0.9090
A = 1.0697
P = 2.7968
MaxY = 0.9260
MinX = 5.0353
Содержание отчета по работе:
Название, цель работы и задание.
Математическое описание, алгоритм(структограмма) и текст программы.
Таблица результатов расчета, графики.
Лабораторная работа №2 «Интерполяция табличных данных»
Цель работы: изучение методов одноинтервальной и многоинтервальной интерполяции.
Задание:
Для 9 узловых точек значений аргумента (температуры) из таблицы 1 [Термодинамические свойства воды и водяного пара С.Л.Ривкин] выбрать 9 значений функций (функцию выбрать из таблицы в соответствии с вариантом)
N варианта |
1, 10, 19 |
2, 11, 20 |
3, 12, 21 |
4, 13, 22 |
5, 14, 23 |
6, 15, 24 |
7, 16, 25 |
8, 17, 26 |
9, 18, 27 |
функция |
P,Па |
V’,м3/кг |
V”,м3/кг |
H’,кДж/кг |
H”,кДж/кг |
R,кДж/кг |
S’,кДж/кгК |
S’,кДж/кгК |
P,бар |
построить график исходной зависимости y(t)
построить график одноинтервальной интерполяции полиномом Лагранжа;
построить график многоинтервальной линейной интерполяционной зависимости
Математическое описание:
Интерполяция - восстановление функции в промежуточных (неузловых) точках по заданному значению аргумента.
Многоинтервальная интерполяция - определение для каждого промежуточного интервала своей интерполяционной зависимости.
Обратная интерполяция - определение значения аргумента по заданному значению функции. Обратная интерполяция выполняется аналогично прямой заменой значений функции значениями аргумента.
Многоинтервальная
кусочно-линейная интерполяция.
Пусть функция задана в n узле (
),
где i=1,..,n. Требуется определить значение
функции в промежуточной точке x. Сначала
определяем номер (i) интервала, к которому
принадлежит x. Затем через две крайние
точки интервала проводим линейную
зависимость, по которой определяем
искомое значение функции. Расчетные
зависимости для равноотстоящих узлов
с шагом h имеют следующий вид:
где int- целая часть числа.
Одноинтервальная интерполяция полином Лагранжа. Интерполяция называется одноинтервальной, когда ищется одна интерполяционная зависимость для всего заданного интервала аргумента. Выполняется через все заданные узлы. Расчетные зависимости имеют вид:
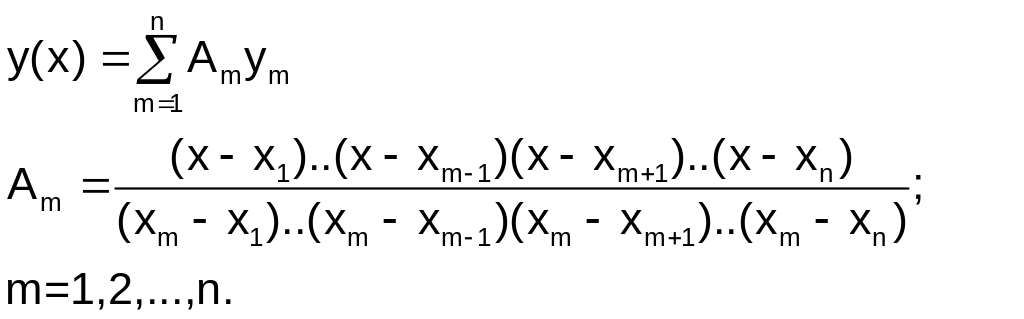
Пример
T,оС |
10 |
50 |
100 |
150 |
200 |
250 |
300 |
350 |
374.12 |
P,кПа |
1.227 |
12.23 |
101.3 |
476 |
1555 |
3978 |
8592 |
16540 |
22115 |
T=[10 50 100 150 200 250 300 350 374.12]%,оС
P=[1.227 12.23 101.3 476 1555 3978 8592 16540 22115]%,кПа
plot(T,P,'o');hold on
T1=[];PL=[];
for t1=11:1:374
for i=1:8
if (t1>T(i))&(t1<T(i+1))
pL=P(i)+(P(i+1)-P(i))/(T(i+1)-T(i))*(t1-T(i));
T1=[T1 t1]
PL=[PL pL]
end
end
end
plot(T1,PL,'r');
T2=[];PLA=[];
for t2=11:1:374
pLA=0
for i=1:9
A=1
for j=1:9
if i~=j
A=A*(t2-T(j))/(T(i)-T(j))
end
end
pLA=pLA+A*P(i);
end
T2=[T2 t2]
PLA=[PLA pLA]
end
plot(T2,PLA,'g');
Содержание отчета по работе:
Название, цель работы и задание.
Математическое описание, алгоритм(структограмма) и текст программы.
Таблица результатов расчета, графики.