2. Производная от параметрически и неявно заданных функций.
О1.
Если
функция
задается в виде системы уравнений
,
то говорят, что функция
задана в параметрическом виде.
Чтобы
продифференцировать параметрически
заданную функцию, надо из первого
уравнения системы найти обратную функцию
и подставить ее во второе уравнение
системы. В результаты этих действий
получается сложная функция, производная
от которой равна
.
Так как производная от обратной функции
связана с производной исходной функции
равенством
,
то формула для производной от параметрически
заданной функции принимает вид:
.
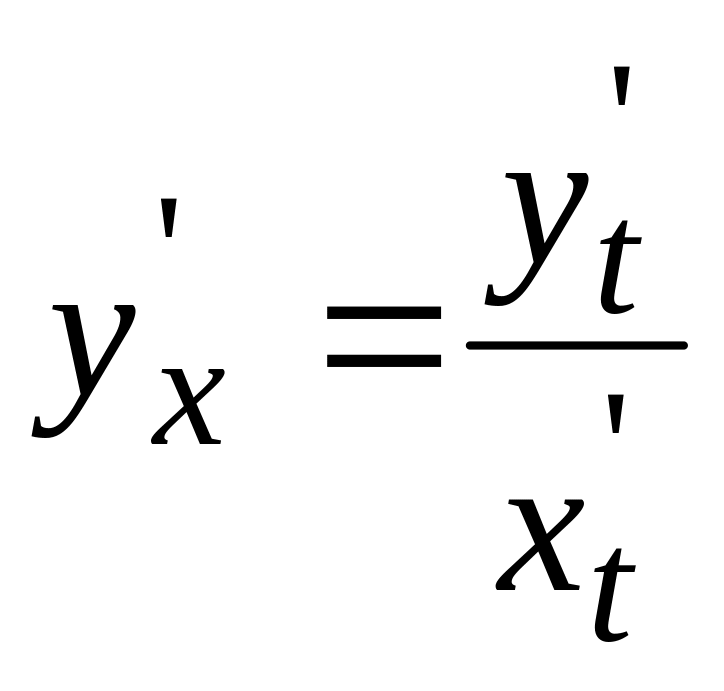Пример
4.
Найти производную функции
.
Вычислим производные от заданных функций по параметру :
.
Следовательно,
.
О2.
Если
функция
задается в виде соотношения
,
из которого нельзя явно выразить
переменную
через
или наоборот, то говорят, что
функция
задана в неявном виде.
Дифференцирование таких функций осуществляется с учетом того факта, что переменная является сложной функцией, т.е. зависит от переменной .
Пример
5.
Найти производную функции
.
Продифференцируем
данное соотношение с учетом вышеизложенного
материала получим
.
Отсюда находим, что
.
С учетом исходного равенства полученное
выражение определяет производную от
неявно заданной функции.
“Дифференциал. Производные и дифференциалы высших порядков”
1. Дифференциал функции. Его свойства и геометрический смысл.
Пусть
функция
дифференцируема в некоторой
–окрестности
точки
,
т.е. существует конечный предел
.
Так как предел конечен, то можно записать
приращение функции в виде
,
где
– бесконечно малая функция в изучаемой
окрестности данной точки. Сравним первое
и второе слагаемые с бесконечно малой
функцией
.
Для первого слагаемого имеем
,
т.е.
оно является бесконечно малой функцией
того же порядка малости, что и величина
.
Для второго слагаемого получаем, что
,
т.е. оно является бесконечно малой
функцией более высокого порядка малости,
чем величина
.
Это означает, что первое слагаемое
является главной частью указанной
суммы.
О1.
Главная
часть приращения функции, линейная
относительно приращения аргумента
,
называется дифференциалом
функции:
.
Пример
1.
Найти дифференциал функции
.
Используя
определение, находим
.
Если
,
то ее дифференциал
.
Следовательно, дифференциал
аргумента равен его приращению.
Отсюда получаем, что дифференциал
функции можно записать в виде
.
Таким образом, для производной можно
ввести новую формулу
.
Такая форма записи производной очень
удобна для вывода различных формул.
Пример
2.
Получить формулу производной от сложной
функции
.
Используя
формулу для производной от функции,
записанную в дифференциалах, найдем
.
Дифференциал функции обладает следующими свойствами:
1.
;
2.
;
3.
;
4.
Дифференциал от сложной функции равен
.
2. Применение дифференциала функции.
Пусть
дана функция
,
тогда при приращении аргумента
функция получает приращение
.
Это приближенное равенство позволяет
по виду функции и известному значению
функции в заданной точке вычислить
значение функции в приращенной точке:
.
Полученное приближенное равенство дает значение функции в приращенной точке тем точнее, чем меньше приращение аргумента.
Пример
3.
Вычислить
.
В
данном примере задана функция
.
В качестве точки
выбираем значение
,
из которого легко извлекается квадратный
корень:
.
Приращенной точкой является точка
.
Таким образом, приращение аргумента
равно
.
Производная от заданной функции согласно
таблице производных
.
Следовательно,
.
Пример
4.
Вычислить
.
В
этом примере
.
Следовательно,
.