“Дифференциальное исчисление. Понятие производной”

1. Приращение аргумента и функции.

Пусть дан график непрерывной функции:

О1. Разность между конечным и начальным значениями аргумента называется его приращением, т.е. .

При этом функция получает приращение .

2. Задачи, приводящие к понятию производной.

1). Физика. Пусть материальная точка движется прямолинейно согласно закону , где - путь, который проходит точка за время . Требуется определить скорость движения точки в момент времени . Обозначим через путь, пройденный за время . Очевидно, что . Средняя скорость, с которой движется точка определяется как . Для того чтобы определить скорость в момент времени , вычислим предел .

2 ). Геометрия. Пусть дан график функции .

Требуется найти такую прямую линию, которая касается графика функции только в одной точке .

О2. Касательной называется предельное положение секущей прямой при стремлении произольным образом.

Вычислим тангенс угла наклона секущей . Следовательно, тангенс угла касательной к положительному направлению оси абсцисс будет равен предельному значению приведенной выше величины .

3. Производная функции. Ее механический и геометрический смысл.

О3. Производной функции в точке называется предел отношения приращения функции к приращению аргумента при стремлении последней вели-

чины к нулю произвольным образом, т. е. .

Из рассмотренных выше задач следует, что с точки зрения механики производная определяет мгновенную скорость движения, а с геометрической точки зрения производная функции равна тангенсу угла наклона касательной к положительному направлению оси абсцисс в заданной точке, в которой вычисляется значение производной.

4. Уравнение касательной и нормали в заданной точке графика функции .

Пусть дан график функции .

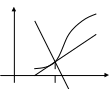
Требуется составить уравнения касательной и нормали в точке . Для составления уравнения касательной воспользуемся уравнением прямой с угловым коэффициентом: . В силу того, что , уравнение касательной имеет вид: . Так как нормаль перпендикулярна к касательной, то ее угловой коэффициент связан с угловым коэффициентом касательной соотношением: . Следовательно, уравнение нормали имеет следующий вид: .

Пример 1. Найти угловой коэффициент касательной в точке к графику функции .

Так как , то вычислим производную функции, используя определение производной:

;

; ; следовательно,

.

Вычислим значение производной в точке , а тем самым и угловой коэффициент касательной в заданной точке .

Пример 2. Составить уравнение касательной для Примера 1 (самостоятельно).