2. Отношения в системном анализе

2.1. Отношения и их свойства

Важную роль в построении моделей играют отношения. Отношения бывают одноместные (унарные), двухместные (бинарные), трехместные (тернарные), n-арные. Наиболее распространены бинарные отношения.

Счетное множество M определено в евклидовом пространстве . Бинарным отношением R на множестве М называется подмножество декартова произведения множества M на самого себя: . Следовательно, бинарное отношение R представляет собой множество упорядоченных пар <x , y> некоторых элементов множества M. Если и и данная упорядоченная пара находится в бинарных отношениях R, то это записывается в виде xRy.

Примерами отношений могут быть x = y – отношение равенства, x > y – отношение порядка со смыслом x больше y ( x “старше” y).

Частным случаем отношений является функция. Если задано отношение F на множестве М так, что для каждого существует ровно один элемент , для которого справедливо отношение . Такое отношение называется функцией . Бинарное отношение может быть задано в виде матриц, графиков или сечений окружностей единичного радиуса.

При матричном задании бинарного отношения R берут двухвходовую матрицу и каждой строке или столбцу взаимно-однозначно сопоставляется элемент множества M. При этом каждое пересечение <x , y> взаимно-однозначно соответствует элементу множества . Если элементы и находятся в отношении M, то на пересечении строки и столбца ставится 1. Например, множество M содержит 5 элементов . Тогда декартово произведение можно представить в виде квадратной матрицы . Допустим отношение R имеет вид:

.

Если первым элементом упорядоченных пар поставить в соответствие строки матрицы, а вторым – столбцы, то матричное представление отношения R будет иметь вид матрицы B:

Матрица B, задающая бинарное дерево, называ-

ется матрицей смежности.

Другой способ матричного задания отношения R заключается в построении такой матрицы , в которой каждому столбцу взаимно-однозначно соответствует элемент множества M, а каждой строке – пара и

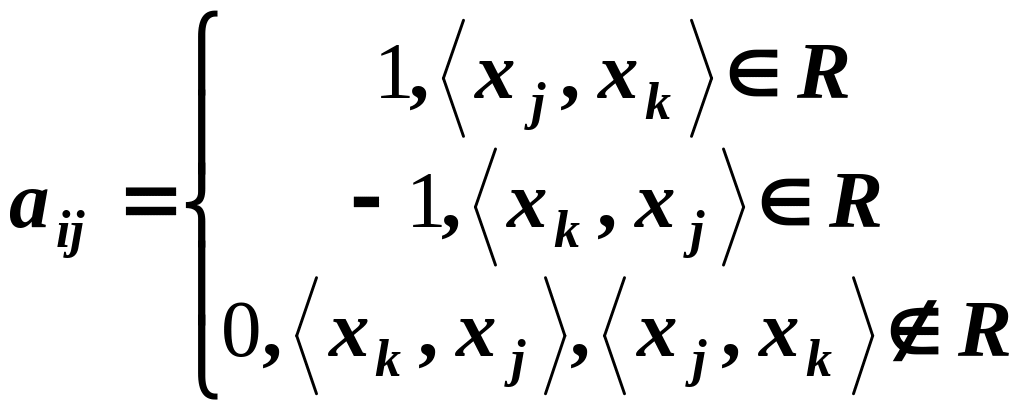
Таким образом, эта матрица будет иметь вид:

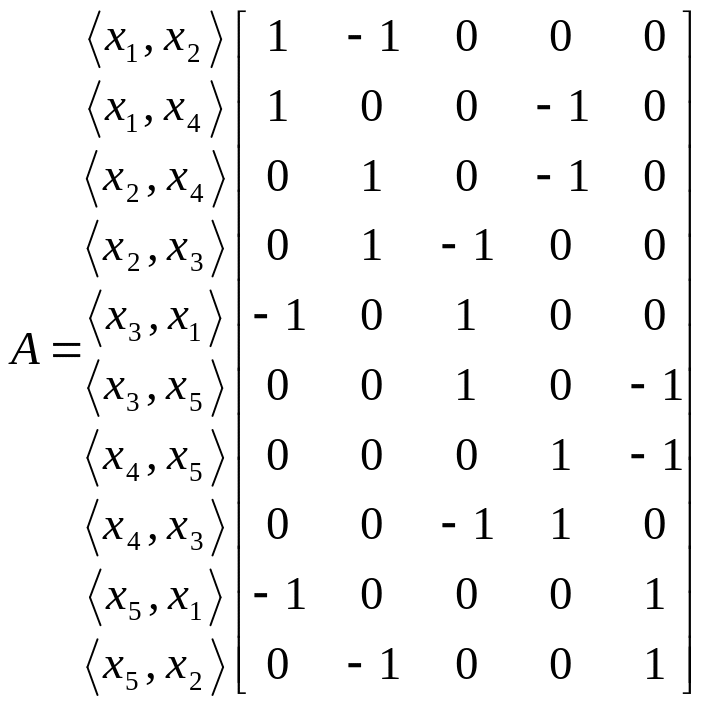
Матрица, заданная таким образом, называется матрицей инциденций.

При задании отношений с помощью графов элементы множества М изображаются точками, а стрелки, направленные от х_i  М к х_j  М, харак-теризуют заданное отношение R. Для приведённого выше примера отношение R будет иметь вид, показанный на рисунке.

Понятие отношений широко используется при анализе систем и в процедуре принятия решений.

2.2. Свойства отношений

Отношение равенства (диагональное отношение) может быть записано таким образом: xEy, которое означает, что x и y один и тот же элемент множества E. Отношение R^-1 называется обратным отношению R на множестве M, если для любых x и y из множества M соотношение xR^-1y равно соотношению yRx.

1. Свойство рефлексивности. Отношение R будет рефлексивным, если имеет место условие (R принадлежит или равно E), т.е. отношение равенства является подмножеством R. Например, отношение выполняется между элементом и им самим. Если x похож на y, то x похож на X. В матричном виде это будет соответствовать условию, если на всех диагоналях стоят единицы, а на графике, если каждое условие имеет петлю.

2. Свойство антирефлексивности. Отношение R называется антирефлексивным, если (пересечение R и E – не пустое множество), т.е. из соотношения xRy следует, что 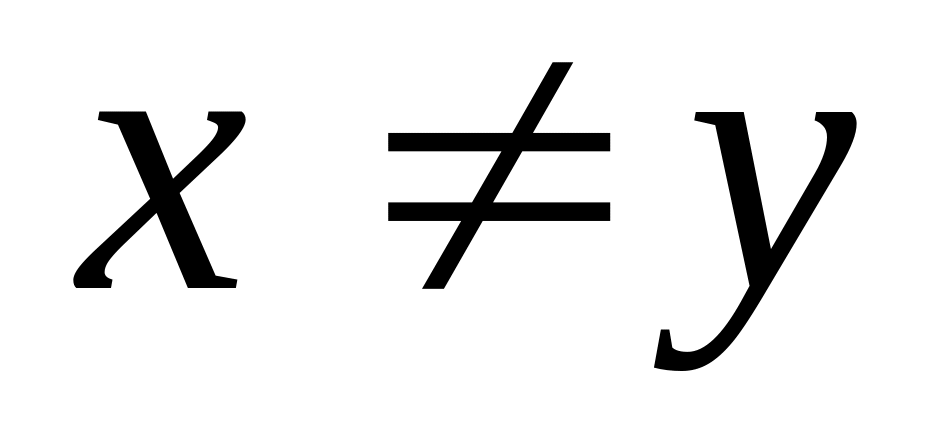. Например:

а) x старше y ;

б) работа y не может быть начата пока не закончится x.

В матрице, задающей отношение антирефлексивности, на всех диагоналях будут стоять нули.

3. Свойство симметричности. Отношение R является симметричным, если выполняется условие: R=R^-1, иначе говоря, если задано xRy, то выполняется и отношение yRx. Например:

а) x похож на y, следовательно и y похож на x;

б) операция x не совместима с операцией y, то, следовательно, и операция y не совместима с операцией x.

В матричном представлении требуется соблюдать симметричность. На графе каждой дуге будет соответствовать встречная дуга и следовательно, это соотношение можно представить неориентированным графом.

4. Свойство асимметричности. Отношение R называется асимметричным, если пересечение прямого и обратного отношения дает пустое множество . Иначе говоря, если xRy и yRx, то одно из них неверно. Например:

а) x подчиняется y, ясно, что y не должен подчиняться x;

б) операция x должна быть выполнена раньше операции y.

5. Свойство антисимметричности. Отношение R называется анти-симметричным, если пересечение прямого и обратного отношения является отношением равенства E. Иначе говоря, оба соотношения xRy и yRx выполняются только тогда, когда x = y. Например:

операция x является частью операции y.

6. Свойство транзитивности. Отношение R является транзитивным, если для любых элементов x, y, z из множества M и соотношений xRy и yRx следует соотношение xRz. Например:

если х больше y (x > y), а y больше z (y > z), то х больше z (x > z).

Отношения подразделяются в зависимости от присущих им свойств на несколько типов, указанных в таблице.

Свойства отношения	Тип отношения
	Эквива-лентность	Толерантность	Строгий порядок	Нестрогий порядок
Рефлексивность	+	+		+
Антирефлексивность			+
Симметричность	+	+
Асимметричность
Антисимметричность				+
Транзитивность	+		+	+

1. Отношения эквивалентности характеризуются 3 свойствами:

• каждый объект эквивалентен самому себе (это отношение рефлексивности);

• если объект x эквивалентен объекту y, то и объект y эквивалентен x (свойство симметричности);

• если объект x эквивалентен объекту y, а объект y эквивалентен объекту z, то значит объект x эквивалентен z (транзитивность).

Отношение R на множестве M называют отношением эквивалентности, если существует разбиение множества R на систему непустых подмножеств {M₁,M₂,…,M_{J ,}…, M_K} таких, что (является объединением) и, с другой стороны, пересечение любых подмножеств (является пересечением пустых множеств) и соотношение xRy выполняется только в тех случаях, когда элементы x и y принадлежат одному классу разбиений.

При отношении эквивалентности подразумевается взаимозаменяемость систем, обычно возможна частичная замена, но существуют и некоторые различия.

2. Отношение сходства используется для оценки «похожести», сначала выясняется мера сходства, а потом их взаимное расположение (объектов). Для понятия схожести вводится понятие толерантности: отношение R на множестве M называется толерантным, если симметрично и рефлексивно.

Например:

если x похож на y , а y похож на z, то это не значит, что x похож на z.

Толерантность более общее понятие, чем эквивалентность.

3. Отношение порядка. Отношение R на множестве M называется отношением строгого порядка, если оно антирефлексивно и транзитивно.

Например:

а) х больше y (x > y), y больше z (y > z);

б) вариант системы х предпочтительней варианта y.

Множество M на котором задано отношение строгого порядка называется упорядоченным множеством.

4. Отношение нестрогого порядка можно представить в виде: . Проявляется рефлексивность, антисимметричность и транзитив-ность, т.е. оба соотношения xRy и yRx выполняются одновременно только тогда, когда .

Например:

а) отношение строгого порядка « > », « »;

б) отношение нестрогого порядка «  ».

Установление типов отношений является основной процедурой анализа систем, позволяющей разбивать систему на подсистемы, упорядочивать подсистемы, идентифицировать их для принятия решений.