Решение

Применим метод комплексных амплитуд. Изобразим расчетную схему без подключенных приборов (рис. 6.6).

Рис. 6.6

еделим комплексное сопротивление цепи:

;

Запишем комплекс действующего значения входного нпряжения:.;

По закону Ома определяем входной ток:

.

Для определения токов ирассчитаем напряжение:

т.к. , то.

Токи исоответственно равны:

;

_...

Определим показания ваттметра:

.

Расчет подтверждает – что активная мощность в ветви с конденсатором отсутствует.

Замечание! При расчете показаний ваттметра положительные направления тока , протекающего через последовательную обмотку ваттметра и напряжения, приложенного к параллельной обмотке ваттметра должны быть одинаковы относительно одноименных зажимов обмоток прибора, обозначенных точкой. Тогда, и стрелка ваттметра отклоняется по шкале вправо. Для построения векторной диаграммы выбираем масштабы напряжений и токов:,.

Векторную диаграмму токов строим согласно первого закона Кирхгофа в комплексной форме ; векторную диаграмму напряжений – согласно второго закона Кирхгофа в комплексной форме. Построение начинаем с вектора тока . Под угломк оси вещественных чисел строим вектор, длина которого равнав выбранном масштабе. Из конца векторастроим вектор тока, что соответствует сложению векторов. Результирующий вектор.

Рис. 6.7

Строим вектора напряжений на всех участках цепи. Построение начинаем из начала координат с вектора напряжения . Длина вектора соответствует действующему значениюв выбранном масштабе напряжений. Направление вектора совпадает с направлением вектора тока, т.к. участокa–d – резистивный. Действующее значение напряжения . Векторопережает ток, на. Сумма векторов напряженийиравна вектору напряжения, что соответствует рассчитанному ранее значению:. Вольтметр, подключенный параллельно участку а – в, покажет действующее значение.

Из конца вектора строим вектор напряжения. Длина вектора равна действующему значениюв выбранном масштабе напряжений. Векторопережает вектор токана.

Длина результирующего вектора равна его действующему значению, начальная фаза, что соответствует исходным данным задачи.

Составим уравнение баланса мощностей в комплексной форме и проверим его выполнение:

.

; .

Активная мощность потребителей:

.

Реактивная мощность потребителей:

Баланс мощностей выполняется.

Ответ: ;;;

; ;

; ;.

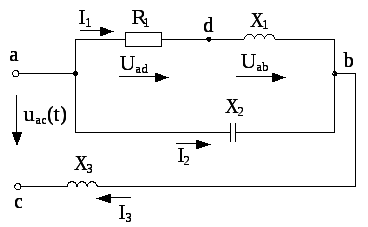
Пример 6.5

	Дано: , ,,,,,,. Для схемы на рис. 6.8 определить напряжение и записать его мгновенное значение.
Рис. 6.8

Решение

Принимаем 1-ый узел за базисный: .

Потенциалы 2–го и 4–го узлов будут соответственно равны:

, .

Составляем уравнение для 3–го узла:

.

Подставим в уравнение численные значения:

;

;

;

.

Решив последнее равенство, получим:

, т.е. .

Запишем мгновенное значение напряжения:

.

Ответ: ;.

Режимы резонанса в электрических цепях Основные теоретические положения

Резонанс – это такой режим работы пассивного двухполюсника, содержащего индуктивности и емкости, при котором угол сдвига фаз между напряжением и током на входе равен нулю ().

Т.к. или, то при резонансе () должно выполняться условиеили.

В зависимости от способа соединений реактивных элементов различают режимы резонанса напряжений в последовательном колебательном контуре и резонанса токов в параллельном колебательном контуре.

Последовательный колебательный контур. Резонанс напряжений

Рассмотрим эквивалентную схему одиночного последовательного колебательного контура (рис.7.1):

Рис.7.1

Параметры ,,называются первичными параметрами контура. Резонансом в последовательном колебательном контуре называют такой режим, в котором цепь ведет себя как активное сопротивление, и ток при этом достигает своего максимального значения.

Условием возникновения резонанса напряжений является равенство нулю реактивной части входного комплексного сопротивления последовательного колебательного контура.

Следовательно, полное комплексное сопротивление равно резистивному сопротивлению: . Ток при резонансе– максимален.

Условие возникновения резонанса напряжений в контуре (рис. 7.1):

.

Резонансная частота или.

Из векторной диаграммы контура в режиме резонанса (рис. 7.2) следует, что входное напряжение равно напряжению на активном сопротивлении.

Рис. 7.2

Характеристическое сопротивление, добротность, затухание контура

Резонансная частота (); характеристическое сопротивление () и добротность () являются вторичными параметрами контура.

а) Характеристическое сопротивление – это сопротивление индуктивности и ёмкости при резонансе:

.

б) Добротность – это отношение максимальной энергии электрического и магнитного полей () к потерям в контуре (₎ или отношение действующих значений напряжений на реактивных элементах к приложенному напряжению в режиме резонанса:

.

Добротность характеризует качество контура и определяет его резонансные свойства. В реальных устройствах к сопротивлению надо прибавитьисточника, что снижает результирующую добротность.

в) Затухание – величина, обратная добротности:

.

г) Полоса частот вблизи резонанса, на границах которой ток снижается до от максимального значениятока при резонансе, определяет абсолютную полосу пропускания контура (рис. 7.3):

,

где играничные частоты полосы пропускания.

Зная ширину полосы пропускания, можно определить добротность контура:

.

Рис. 7.3

Рассмотрим, как определить резонансную частоту колебательного контура рис. 7.4

Рис. 7.4

Особенностью цепи является наличие шунта , подключенного параллельно к емкости, который изменяет сопротивление цепи.

Резонансную частоту определим из условия равенства нулю эквивалентного реактивного сопротивления контура. Запишем полное комплексное сопротивление цепи, выделим действительную и мнимую части:

.

В режиме резонанса (полное сопротивление носит активный характер), следовательно:

или ,

откуда .

Векторная диаграмма колебательного контура (рис. 7.4) в режиме резонанса представлена на рис. 7.5.

Рис. 7.5

Напряжение на входе .

На диаграмме видно, что входное напряжение совпадает по фазе с током, что соответствует условию режима резонанса.

Параллельный колебательный контур. Резонанс токов

Эквивалентные схемы параллельных колебательных контуров представлены на рис. 7.6 а – в.

Рис. 7.6. а	Рис. 7.6. б	Рис. 7.6. в

Явление резонанса в схеме образованной двумя параллельными ветвями с разнохарактерными сопротивлениями, называется резонансом токов. Условием резонанса токов является равенство нулю реактивной части полной комплексной проводимости параллельного колебательного контура.

Проводимости ветвей схемы рис. 7.6. в) равны:

;

,

где ,.

.

Т.к. при резонансе , то полная проводимость должна носить активный характер, что возможно при, т.е.

.

Решив это равенство относительно резонансной частоты , получим:

.

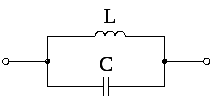
В частном случае идеального контура (рис. 7.6. а) .

Полная проводимость идеального контура , следовательно. Таким образом,идеальный контур при резонансе токов эквивалентен разрыву цепи.