
- •Теоретический раздел
- •Элементы электрических цепей.
- •Положительные направления тока и напряжения.
- •Источник напряжения и источник тока.
- •Сопротивление.
- •Индуктивность.
- •Емкость.
- •Законы электрических цепей
- •Топологические элементы схемы: ветви, узлы, контуры.
- •Распределение потенциала вдоль участка ветви. Потенциальная диаграмма.
- •Обобщенный закон Ома.
- •Законы Кирхгофа.
- •Составление баланса мощностей.
- •Преобразование схем электрических цепей
- •Преобразование схем электрических цепей.
- •Преобразование звезды в эквивалентный треугольник.
- •Методы расчета сложных электрических цепей
- •Методы расчета сложных электрических цепей.
- •Входные и передаточные проводимости.
- •Метод контурных токов.
- •Метод узловых напряжений.
- •Теоремы линейных цепей
- •Теоремы линейных цепей.
- •Электрические цепи периодического синусоидального тока и напряжения.
- •Мощность в электрических цепях периодического синусоидального тока.
- •Реактивные двухполюсники.
- •I класс.
- •III класс.
- •IV класс.
- •Режимы резонанса в электрических цепях
- •Резонанс напряжений.
- •Резонанс токов.
- •Индуктивно связанные электрические цепи Индуктивная связь. Эдс взаимной индукции. Взаимная индуктивность. Коэффициент связи .
- •Одноименные зажимы индуктивно связанных катушек.
- •Последовательное соединение индуктивно связанных катушек при согласном включении.
- •Последовательное соединение индуктивно связанных катушек при встречном включении.
- •Параллельное соединение индуктивно связанных катушек
- •Развязка индуктивных связей
- •Воздушный трансформатор
- •Практический раздел Индивидуальные практические работы Выбор варианта
- •Порядок выполнения лабораторных работ (индивидуальных практических работ) по курсу "тэц"
- •Оформление протокола и защита лабораторных работ
- •Правила оформления протокола лабораторных работ
- •Содержание протокола
- •Индивидуальная практическая работа № 1 исследование цепи постоянного тока методом узловых напряжений и методом эквивалентного генератора
- •Основные теоретические положения
- •Последовательность выполнения работы
- •Индивидуальная практическая работа № 2 исследование простых цепей синусоидального тока
- •Основные теоретические положения
- •Последовательность выполнения работы
- •Литература для выполнения индивидуальных практических работ
- •Контрольные работы Выбор варианта
- •Контрольная работа №1
- •Контрольная работа №2
- •Внешние ресурсы
- •Практикум
- •Закон Ома, законы Кирхгофа
- •Основные теоретические положения. Закон Ома
- •Законы Кирхгофа
- •Примеры расчета линейных электрических цепей по законам Ома и Кирхгофа
- •Решение
- •Решение
- •Метод наложения Основные теоретические положения
- •Примеры расчета линейных электрических цепей методом наложения
- •Решение
- •Метод контурных токов Основные теоретические положения
- •Примеры расчета линейных электрических цепей методом контурных токов
- •Решение
- •Метод узловых напряжений Основные теоретические положения
- •Примеры расчета линейных электрических цепей методом узловых напряжений
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Метод эквивалентного генератора Основные теоретические положения
- •Примеры расчета линейных электрических цепей методом эквивалентного генератора
- •Решение
- •Решение
- •Электрические цепи однофазного синусоидального тока. Комплексный метод расчёта электрических цепей. Баланс мощностей в цепях однофазного синусоидального тока. Основные теоретические положения
- •Синусоидальный ток в однородных идеальных элементах: резисторе, индуктивности, ёмкости. Временные и векторные диаграммы.
- •Баланс мощностей в цепях переменного тока
- •Примеры расчёта цепей однофазного синусоидального тока
- •Решение
- •Решение
- •Пример 6.3
- •Решение
- •Решение
- •Решение
- •Режимы резонанса в электрических цепях Основные теоретические положения
- •Примеры расчета электрических цепей в режиме резонанса
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Цепи с индуктивно–связанными элементами Основные теоретические положения
- •Примеры расчета схем с индуктивно–связанными элементами
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самоконтроля
- •Экзаменационные вопросы
- •Часть 1
Примеры расчета линейных электрических цепей методом наложения
Пример 2.1
Дано:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Определить все токи методом наложения в схеме рис. 2.1.
|
|
|
|
Рис. 2.1 |
Рис. 2.2 |
Решение
1)
Заменяем источник Э.Д.С. E
короткозамкнутым участком (т.к. его
![]() )
(схема рис. 2.2).
)
(схема рис. 2.2).
Т.к. конфигурация цепи изменилась, то в цепи рис. 2.2 протекают токи, отличные от токов цепи рис. 2.1. Их называют первыми частичными токами и обозначают одним штрихом. Схему цепи рис. 2.2 более наглядно представим на рис. 2.3. Токи рассчитаем, применяя правило плеч и первый закон Кирхгофа:
 ;
;
![]() ;
;
 ;
;
![]() ;
;
![]() .
.
Ток
![]() протекает по короткозамкнутому участку
(его сопротивление равно нулю).
протекает по короткозамкнутому участку
(его сопротивление равно нулю).
Запомнить! Ток в ветви, сопротивление которой равно нулю, определяют по первому закону Кирхгофа.
2) Разорвем ветвь с источником тока J. Токи, протекающие в цепи рис. 2.4, называют вторыми частичными токами и обозначают двумя штрихами.
|
|
|
|
Рис. 2.3 |
Рис. 2.4 |
Напряжение,
создаваемое Э.Д.С. E,
приложено к двум параллельным ветвям.
Токи
![]() и
и![]() определим по закону Ома:
определим по закону Ома:
 ;
;
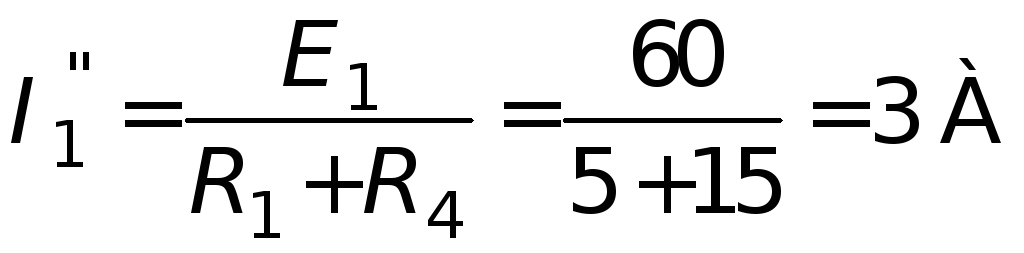 ;
;
![]() .
.
Искомые токи найдем как алгебраическую (т.е. с учетом направлений) сумму частичных токов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Метод контурных токов Основные теоретические положения
Метод контурных токов – один из основных и широко применяемых на практике методов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно.
Контурные токи, проходя через узел, не меняют своего значения и направления. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
Число уравнений, составляемых по методу контурных токов, определяется по формуле:
![]() .
.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
Если заданная электрическая цепь содержит n независимых контуров, то на основании второго закона Кирхгофа получается n контурных уравнений:
|
|
(3.1) |
где
![]() –
собственное сопротивление контура,
равное сумме сопротивлений, по которым
протекает контурный ток
–
собственное сопротивление контура,
равное сумме сопротивлений, по которым
протекает контурный ток![]() (
(![]() – величина положительная),
– величина положительная),
![]() –взаимное
сопротивление между двумя смежными
контурами, которое может быть положительным
или отрицательным в зависимости от
того, совпадают ли направления протекающих
по ним контурных токов,
–взаимное
сопротивление между двумя смежными
контурами, которое может быть положительным
или отрицательным в зависимости от
того, совпадают ли направления протекающих
по ним контурных токов,
![]() –контурная
Э.Д.С., равная алгебраической сумме
Э.Д.С., входящих в данный контур.
–контурная
Э.Д.С., равная алгебраической сумме
Э.Д.С., входящих в данный контур.
После решения системы (3.1) ток в ветви определяют как алгебраическую сумму контурных токов, протекающих через данную ветвь.
Примеры расчета линейных электрических цепей методом контурных токов
Пример 3.1
Составить
уравнение по методу контурных токов и
определить токи во всех ветвях схемы
(рис. 3.1), если
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
На примере данной задачи покажем как пользоваться методом контурных токов, если схема содержит источники тока.
|
|
|
Рис. 3.1 |
Решение
В
цепи четыре независимых контура,
следовательно обозначим четыре контурных
тока:
![]() ,
,![]() ,
,![]() ,
,![]() и
их положительные направления.
и
их положительные направления.
Токи
![]() ,
,![]() ,
,![]() ,
протекают через источники тока
,
протекают через источники тока![]()
![]()
![]() соответственно.
Следовательно:
соответственно.
Следовательно:
![]() ;
;![]() ;
;![]() ;
;
В
данной задаче необходимо определить
один контурный ток
![]() ,
следовательно, составим только одно
уравнение:
,
следовательно, составим только одно
уравнение:
![]() ,
,
Откуда
![]() .
.
Токи ветвей определим как алгебраическую сумму контурных токов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Правильность решения задачи проверим, составив уравнение по второму закону Кирхгофа для контура 4 (контур обходим по часовой стрелке):
![]() ;
;
![]() ;
;
![]() .
.
Второй закон Кирхгофа выполняется.
Ответ:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Пример 3.2
|
|
Дано:
Определить токи в схеме рис. 3.2 методом контурных токов.
Решение
Выбираем
направления контурных токов. Контурные
токи
|
соответственно:
![]() ;
;![]() .
Для решения задачи
необходимо
составить одно уравнение для неизвестного
контурного тока
.
Для решения задачи
необходимо
составить одно уравнение для неизвестного
контурного тока
![]() :
:
![]() .
.
Решив его, получаем:
 .
.
Токи в ветвях схемы определяем как алгебраическую сумму контурных токов, проходящих через каждую ветвь:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.



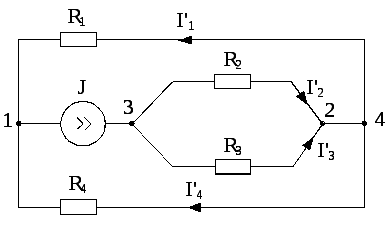



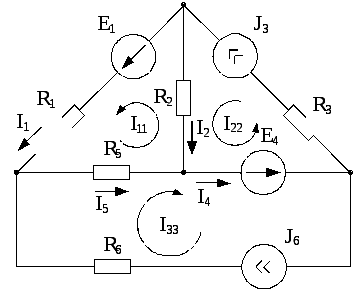 Рис.
3.2
Рис.
3.2