Резонанс токов.

Этот вид резонанса бывает в электрических цепях, где есть параллельное соединение индуктивности L и емкости C.

Схема а) – идеальная, остальные наиболее распространены, рассмотрим схему г).

Как известно, при резонансе входное сопротивление схемы носит активный характер и угол сдвига фаз равен нулю

Найдем входное сопротивление нашей схемы.

где

Легче найти Z_вх через проводимость.

где

Условие резонанса в цепи

При R₁‹‹X_L, R₂‹‹X_C (высокодобротный контур)

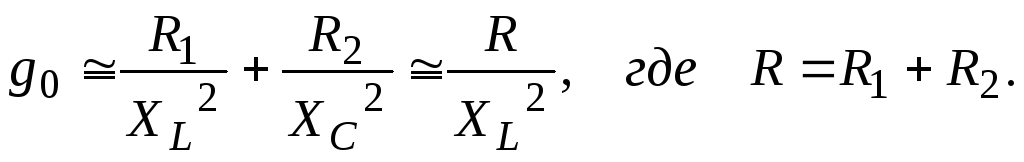
Если φ=0, то b=0.

или

при R₁‹‹X_L, R₂‹‹X_C

Из условия b=0 найдем резонансную частоту

Анализируя выражение ω_p, можно видеть:

• в высокодобротных контурах (R₁‹‹X_L, R₂‹‹X_C) ω_p=ω₀ (частота резонансов токов совпадает с частотой резонанса напряжений);

• в низкодобротных контурах (R₁≥X_L, R₂≥X_C) резонанс токов наступает при ω_p или его нет.

Далее рассматриваем высокодобротные контура. На резонансной частоте ω_p=ω₀имеем:

Видно, что на резонансной частоте проводимость g₀ очень мала, а резонансное входное сопротивление контура R_p очень велико (в идеальном случае R_p=).

Как и в контуре резонанса напряжений, в данном контуре происходят колебания энергии между магнитным полем катушки и электрическим полем конденсатора, в идеальном контуре, при отключении его от источника, эти колебания будут происходить бесконечно, реально они затухают, но тем медленнее, чем выше добротность контура.

В момент резонанса на _p=₀ имеем

Векторная диаграмма будет:

В идеальном контуре

В реальном высокодобротном контуре мало,, поэтому этот вид резонанса и назвалирезонансом токов.

Часто данный контур питают от источника тока, напряжение на контуре, в этом случае, может быть большим.

Видно, что в высокодобротном контуре (R₁X_L, R₂X_C) U_аб, I_L и I_C – большие величины, _L и _C – близки к 90.

Рассмотрим поведение параметров контура резонанса токов при расстройках

Векторные диаграммы при расстройках

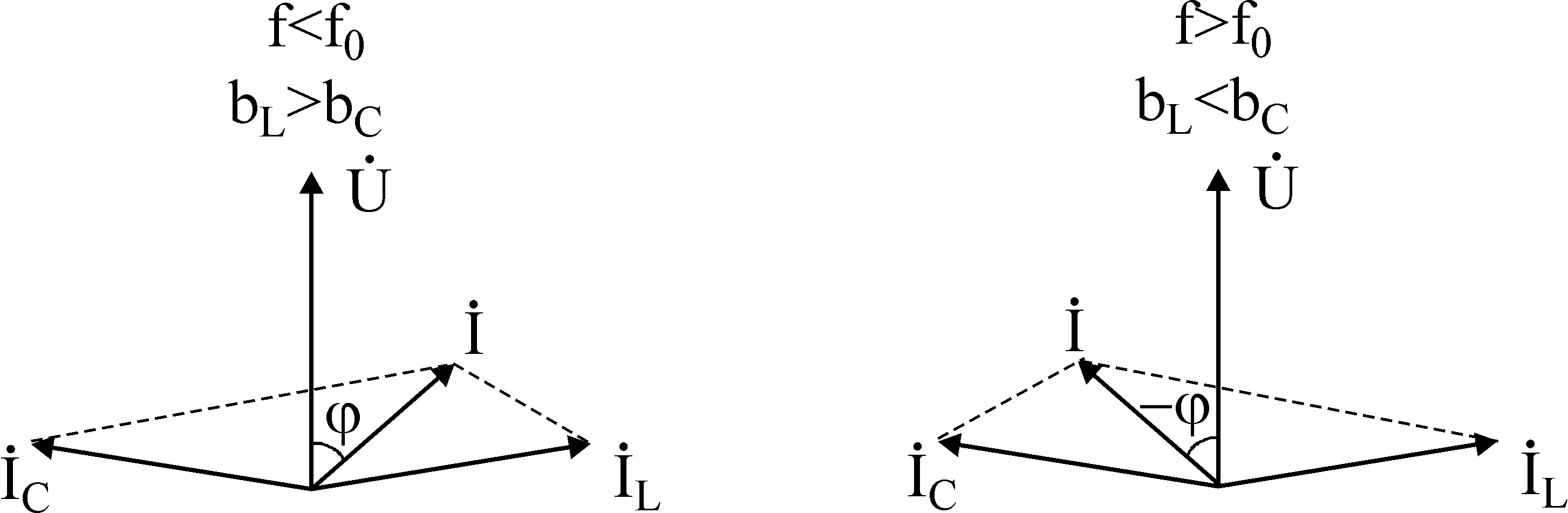
Полоса пропускания контура с резонансом токов – полоса частот, на границах которой ток I увеличивается, а напряжение уменьшается враз.

Часто контур резонанса токов применяется с шунтирующим сопротивлением

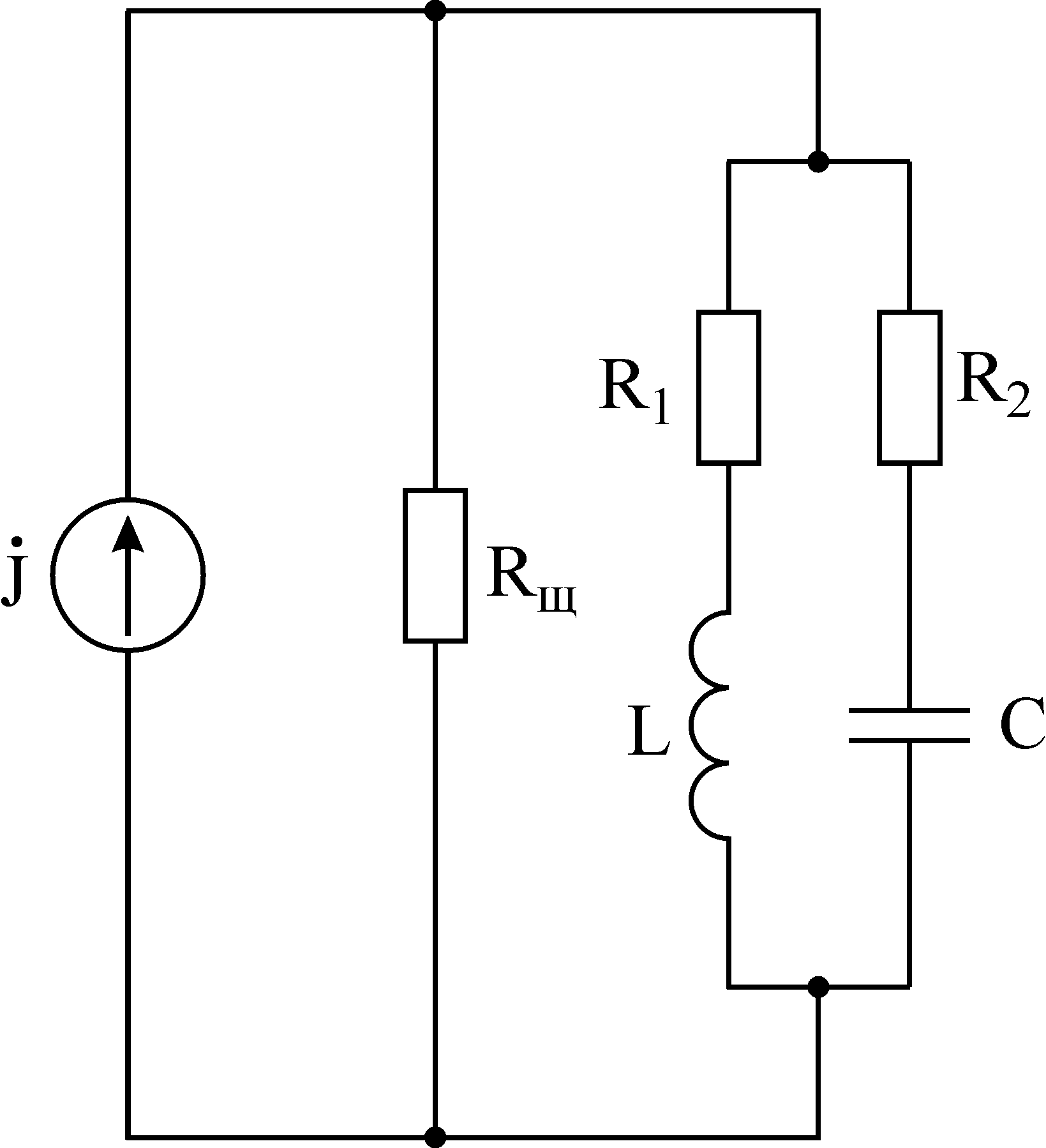
Видим, что в этом случае, чем больше R_ш, тем больше Q_э (ближе к Q), т.е. нужен источник тока с малой внутренней проводимостью (большим внутренним сопротивлением).

Выводы по резонансу токов:

• этот вид резонанса имеет место при параллельном соединении L и C; в высокодобротном контуре ; условие резонанса в=0;

• в высокодобротном контуре тока в ветвях в величину добротности превышают ток в неразветвленной части схемы;

• низкоомные сопротивления ветвей контура (R₁+R₂=R) преобразуются в высокоомное входное сопротивление контура , при помощиR_ш его можно регулировать.

Индуктивно связанные электрические цепи Индуктивная связь. Эдс взаимной индукции. Взаимная индуктивность. Коэффициент связи .

Электрические цепи называются связанными, если процессы в них влияют друг на друга. Это влияние может осуществляться посредством общего электрического или магнитного поля. В последствии случая цепи называются индуктивно связанными.

Рассмотрим две катушки, расположенные рядом (рис. 5.1.а)

Рис.5.1

Протекающий в первой катушке с числом витков W₁ и индуктивности L₁ ток i₁ вызывает магнитный поток Ф₁₁. ЭДС, наводящаяся в первой катушке под воздействием Ф₁₁,

называется ЭДС самоиндукции, где - потокосцепление самоиндукции.

Часть потока Ф₁₂ охватывает находящуюся рядом вторую катушку с числом витков W₂ и индуктивностью L₂ и наводит в ней ЭДС взаимной индукции. W – одинаков.

, где – потокосцепления взаимной индукции ,-взаимная индуктивность между первой и второй катушками.

Протекающий во второй катушке ток i₂ (рис.5.1.б), вызывает поток Ф₂₂ .

Часть этого потока, охватывает витки первой катушки. По аналогии можем записать

,

,

где e₂-ЭДС самоиндукции второй катушки,

–потокосцепление самоиндукции второй катушки,

e₂₁ – ЭДС взаимной индукции, наводящаяся в первой катушке под воздействием потока Ф₂₁.

М₂₁ – взаимная индуктивность между второй и первой катушками.

Если обе катушки находятся в среде не обладающей никакими аномальными свойствами, то взаимные индуктивности М₁₂ и М₂₁ оказываются равными

М₁₂=М₂₁=М. Взаимная индуктивность М – размерная величина и по ней трудно судить о степени взаимного влияния катушек друг на друга.

Для оценки степени связи катушек пользуются относительной величиной – коэффициентом связи k, который определяется как среднее геометрическое из отношения потокосцепления взаимной индукции к потокосцеплениям самоиндукции.

Коэффициент k может принимать значения в пределах от 0 до 1.

При k=0 между катушками не существует индуктивной связи, при k=1 – поток одной катушки полностью охватывает витки второй катушки Ф₁₂=Ф₁₁, Ф₂₁=Ф₂₂.

Величина k зависит от:

– расстояния между катушками,

– взаимной ориентации катушек в пространстве,

– магнитных свойств среды, в которой расположены катушки.