Режимы резонанса в электрических цепях

Как и в физике, режим резонанса в электрической цепи наступает при совпадении частот колебаний – частоты внешнего воздействия и частоты собственных колебаний устройства (в данном случае электрической цепи). Но в электротехнике есть свои особенности.

В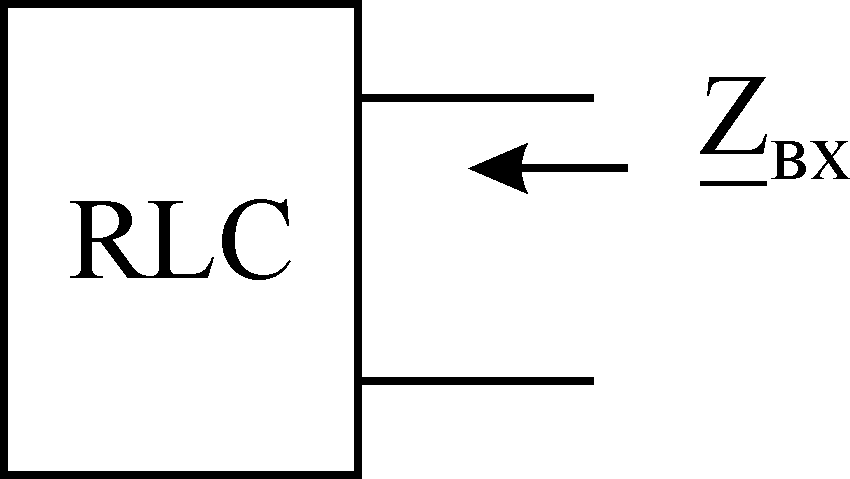электрической цепи должны быть емкости (конденсаторы)C и индуктивные катушки L.

Резонанс в электрической цепи имеет место, если входное сопротивление цепи , т.е. если входное сопротивление носит активный характер, а это значит, что на резонансной частотена входе в схему ток и напряжение совпадает по фазе.

Кроме того, в момент резонанса входное сопротивление может быть равно нулю (это идеальный случай) или минимальное, а может быть равно бесконечности (опять идеальный случай) или очень большое, максимальное. Эти два случая разделили:

- резонанс напряжений,

- резонанс токов.

Почему так назвали, увидим из рассмотрения конкретных схем.

Резонанс напряжений.

Этот вид резонанса бывает в цепях, где имеется последовательное соединение индуктивности L и емкости C.

Комплексное сопротивление данной схемы

Известно, что изависят от частоты, значит на какой-то частоте, назовем ее резонанснойf₀, эти сопротивления будут равны, а входное сопротивление контура будет равно R.

Эту частоту легко определить

На частоте f₀ X=X_L-X_C=0.

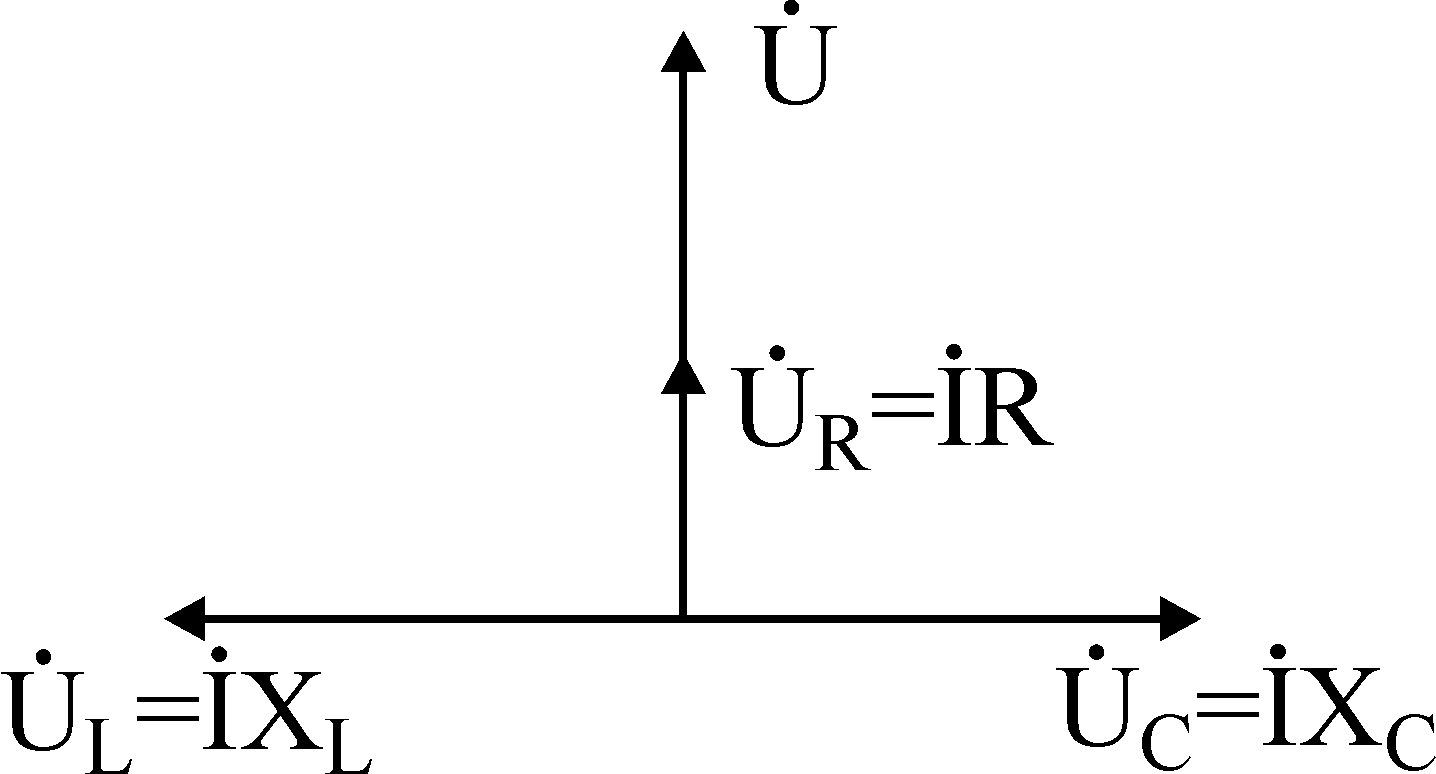
Рассмотрим, что происходит в этот момент в схеме. Допустим, что U(t)=U_msin₀t, тогда ток

Так как на f₀ X_L=X_C получаем

Что же происходит в нашем контуре на резонансной частоте f₀?

Известно, что энергия в катушке равна энергия в конденсаторе

При резонансе X_L=X_C, значит W_Lm=W_Cm. Значит вся энергия источника расходуется в активном сопротивлении, а в идеале, когда R=0 и контур отключить от источника и замкнуть, происходит обмен энергией между катушкой и конденсатором бесконечно долго. Но как только появилось активное сопротивление (а у катушки оно всегда есть). За счет потерь Джоуля – Ленца (I²R) происходит уменьшение энергии, причем чем меньше R, тем дольше идет процесс. Поэтому в резонансном контуре ввели понятие добротности Q.

Добротность представляет собой отношение максимальной энергии W_Lm=W_Cm к потерям в контуре P=I²R.

Вес контура условно разделили на высокодобротные Q10 или X_L0=X_C0R10 и низкодобротные Q10.

Кроме этого, на резонансной частоте f_p имеем X_L=X_C,

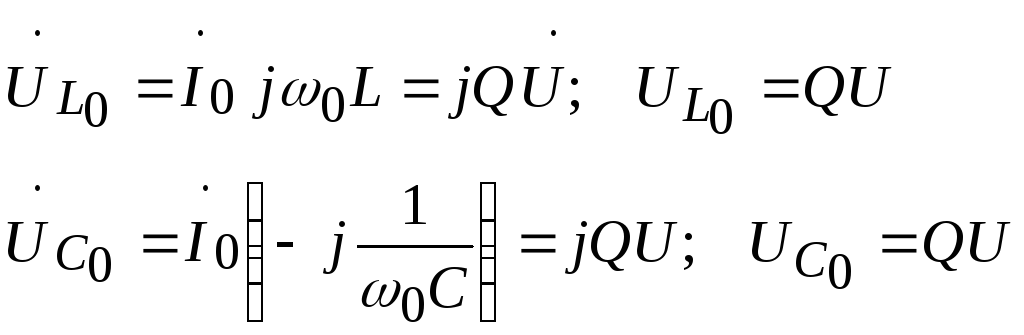
Видно, что в высокодобротных контурах, напряжение на катушке и емкости в величину добротности превышает входное напряжение. Поэтому резонанс при последовательном соединенииL и C назвали резонансом напряжений, и этот контур часто используется как усилитель напряжения.

Рассмотрим поведение различных параметров контура в зависимости от частоты. Зависимость от частоты тока, напряжения, сопротивлений называется амплитудо-частотными характеристиками (АЧХ), зависимость фазы, угол сдвига фаз от частоты называется фазо-частотной характеристикой (ФЧХ).

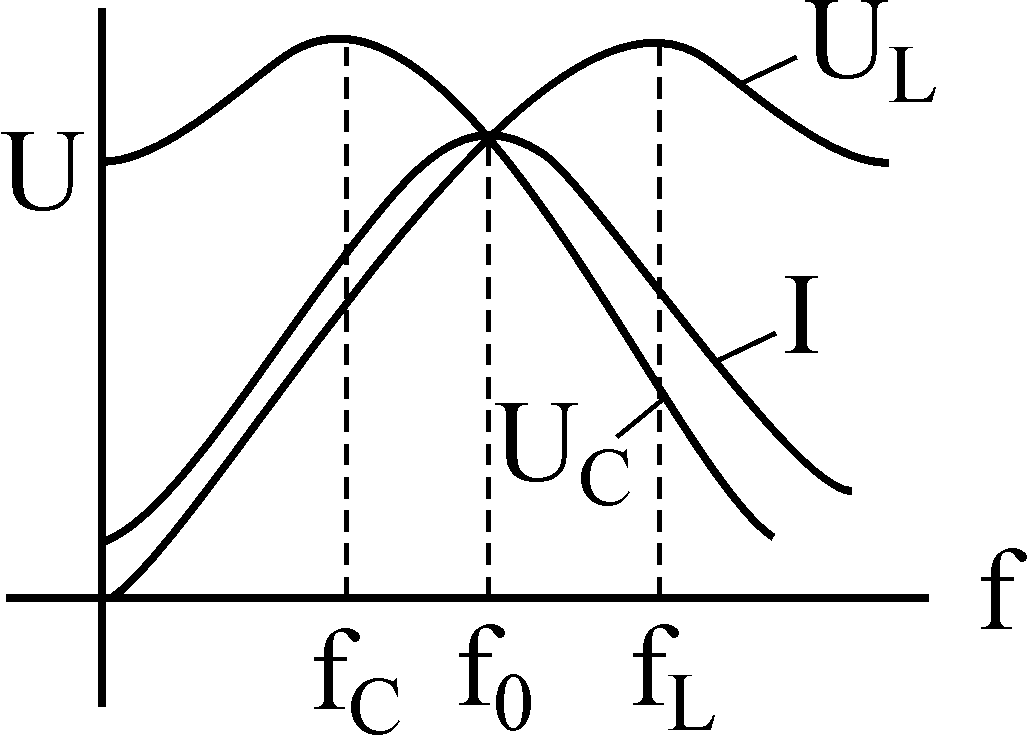
Максимум U_C и U_L наступают при

где (величина, обратная добротности).

Векторные диаграммы при

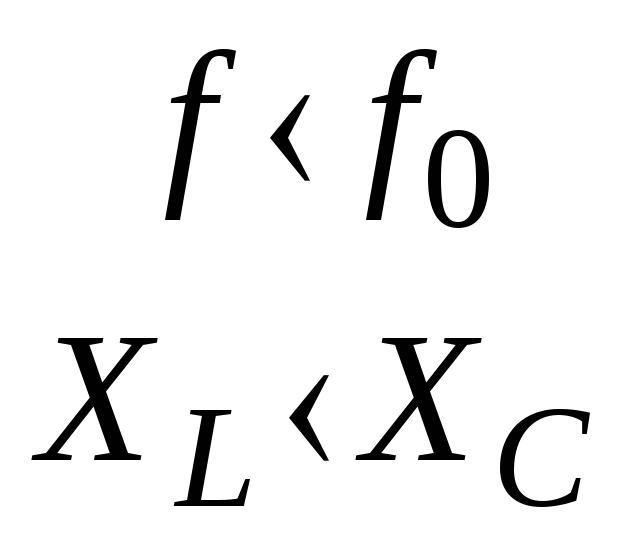
При рассмотрении резонансов используется понятие полоса пропускания-это полоса частот, на границах которых мощность, поглощаемая контуром, в два раза меньше мощности, поглощаемой контуром, на резонансной частоте.

На частотах, граничных полосе пропускания, ток или напряжения изменяются в раз, а.

Очень часто интересно поведение различных параметров контура в узкой полосе частот вблизи резонансной частоты.

Имеем –

резонансная частота -

абсолютная расстройка -

относительная расстройка -

обобщенная расстройка (кси) –

(при этом все расстройки положительны, при ff₀, отрицательны при f  f₀, при очень малых расстройках (),).

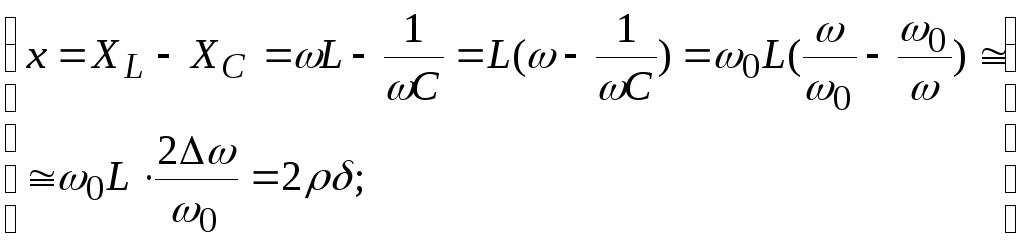
Теперь можно построить характеристики I, Z,  в зависимости от .

При этом можно видеть, что зависимости от относительной расстройки различаются по величине добротностиQ, а зависимости от обобщенной расстройки одинаковы для всех контуров.

Чем больше добротность, тем острее кривая и уже полоса пропускания.

Для полосы пропускания можно видеть:

- абсолютная полоса пропускания,

- относительная полоса пропускания.

На границах полосы пропускания .

Как отмечалось, контур резонанса напряжений часто используется как усилитель напряжения.

Повышенное напряжение чаще снимается с емкости.

Заменив параллельное соединение C и R_Н последовательным, получим схему:

где . (для высокодобротных контуровR₁X_L=X_C; R_НX_C).

При этом добротность контура с R_Н несколько меньше добротности контура.

Выводы по резонансу напряжений:

• этот вид резонанса имеет место при последовательном соединении R, L, C; резонансная частота , условие резонансаX_L=X_C; 

• напряжения на L и C примерно равны U_L=U_C=QU и зависят от величины добротности контура Q=X_L/R, при Q10 имеем хорошие резонансные кривые и узкую полосу пропускания.