Электрические цепи периодического синусоидального тока и напряжения.

Электрический ток и напряжение изменяющиеся во времени по какому-либо закону называют переменными.

Если форма кривой переменного тока и напряжения повторяется через равные промежутки времени, то их называют периодическими.

Наименьшее время, через которое повторяется форма переменного тока и напряжения, называют периодом, обозначают Т и измеряют в с.

Число периодов Т в 1 секунду называют частотой f переменного тока и напряжения и дана размерность герц (Гц).

, Гц

Простейшими периодическими переменными током и напряжением являются вырабатываемые генераторами всех видов электростанций напряжения и тока (энергия) синусоидальной формы.

, А

, B

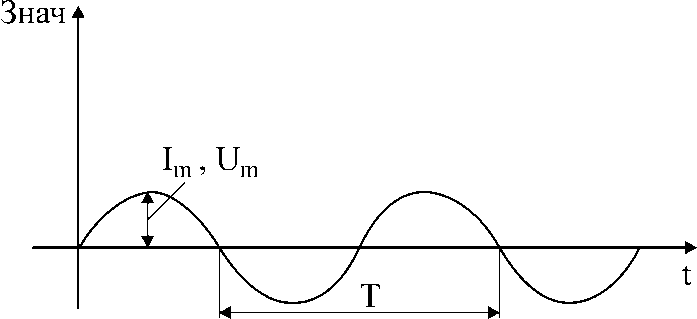
Здесь обозначают:

i(t), u(t) – мгновенное значение тока и напряжения;

I_m, U_m – амплитудные значения тока и напряжения;

_i, _u – начальная фаза тока и напряжения, герц;

= 2f – угловая частота, с^-1.

Разницу начальных фаз напряжения и тока обозначили =_u–_i и назвали угол сдвига фаз.

Периодические ток и напряжение характеризуют еще понятиями среднего и действующего значения.

Среднее значение – это среднее значение за период. Так как у синусоидальной функции оно равно нулю ( ), у синусоидального тока и напряжения за среднее значение определяют значение за полпериода ().

, А

, В

или I_ср=0,64 I_m, U_ср=0,64 U_m.

Действующее значение периодической синусоидальной функции – это среднеквадратичное значение за период.

Тогда

, A

, B

Необходимо запомнить – разница между амплитудным и действующим значением периодического синусоидального тока и напряжения – .

Измерительные приборы (амперметры. вольтметры) магнитоэлектрической системы показывают среднее (I_ср, U_ср) значение синусоидального тока и напряжения i(t), u(t).

Измерительные приборы (амперметры. вольтметры) электромагнитной, электродинамической, тепловой систем показывают действующее значение (I, U) синусоидального тока и напряжения i(t), u(t).

По действующему значению I периодического синусоидального тока судят о его тепловом воздействии: действующее значение I равно постоянному току I₀, который выделяет в активном сопротивлении R за один период Т столько же тепла, что и .

(I²R=I₀²R).

Мощность в электрических цепях периодического синусоидального тока.

Мгновенное значение мощности.

, BA

Здесь обозначили и назвали:

UI=S – полная мощность, ВА;

UICos =P – активная мощность, Вт;

UISin =Q – реактивная мощность, ВАР.

Рассмотрим поведение периодических синусоидальных токов и напряжений в отдельных элементах электрических цепей.

Активное сопротивление R.

U_m= I_mR; _u=_i; =_u–_I=0

т.е. в активном сопротивлении угол сдвига фаз  равен нулю, значит напряжение и ток в активном сопротивлении совпадает по фазе (_R=_u–_i=0).

Среднее значение за период – активная мощность

И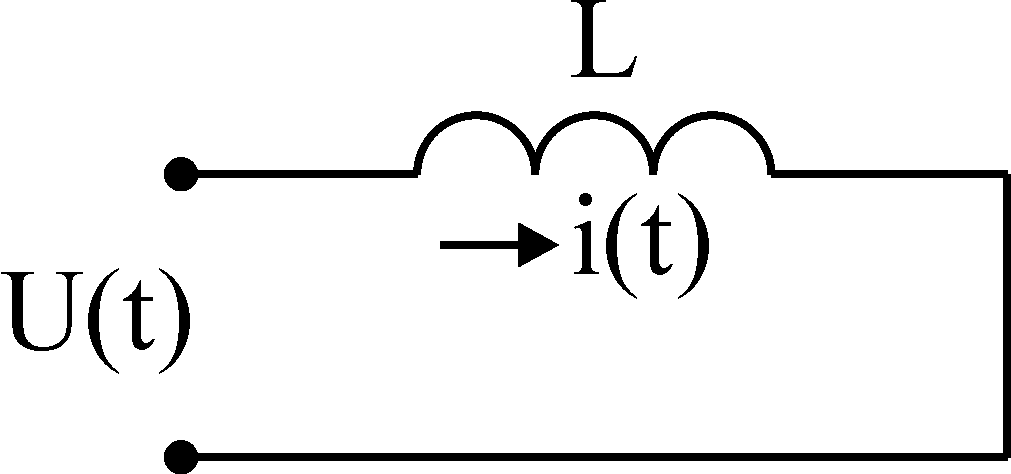ндуктивностьL

, ,

а величину X_L=L называют индуктивным сопротивлением и дали размерность Ом, величина обратная X_L – индуктивная проводимость .

Здесь получили два важных момента:

• индуктивное сопротивление X_L=L=2fL, Ом;

• на идеальной индуктивности L угол сдвига фаз , т.е. напряжениеU_L(t) опережает ток в индуктивности на 90.

.

Видно, что активная мощность p_L=0, a Q_L= UI = I²X_L

Емкость C

, b_c – емкостная проводимость;

–емкостное сопротивление, размерность – Ом.

.

Получили две важных момента:

• емкостное сопротивление и проводимость

,

• на идеальной емкости С угол сдвига фаз , т.е. напряжение отстает от тока на угол 90.

Как и на индуктивности, на емкости активная мощность P_С=0, а реактивная Q_С= UI = I²X_С

Если токи и напряжения на R, L и С изобразить в виде векторов, то можно видеть:

_R = 0

_L = +90

_С = –90

Наша задача – рассчитать электрическую цепь, т.е. определить токи в ветвях и напряжения между узлами и на элементах, при действии периодических синусоидальных токов и напряжений.

Рассмотрим простейшую цепь – последовательное соединение элементов R, L, C.

Допустим, что , т.е. . Тогда по второму закону Кирхгофа:

где величину X_L­–X_C=X назвали реактивным сопротивлением.

(Видно, что X имеет знак  , в зависимости что больше X_L­ или X_C).

Используя тригонометрию, можно видеть:

;

,

где , назвали – полное сопротивление

Если изобразить расчет напряжения в цепи в виде векторов, то получим:

–цепь имеет индуктивный характер.

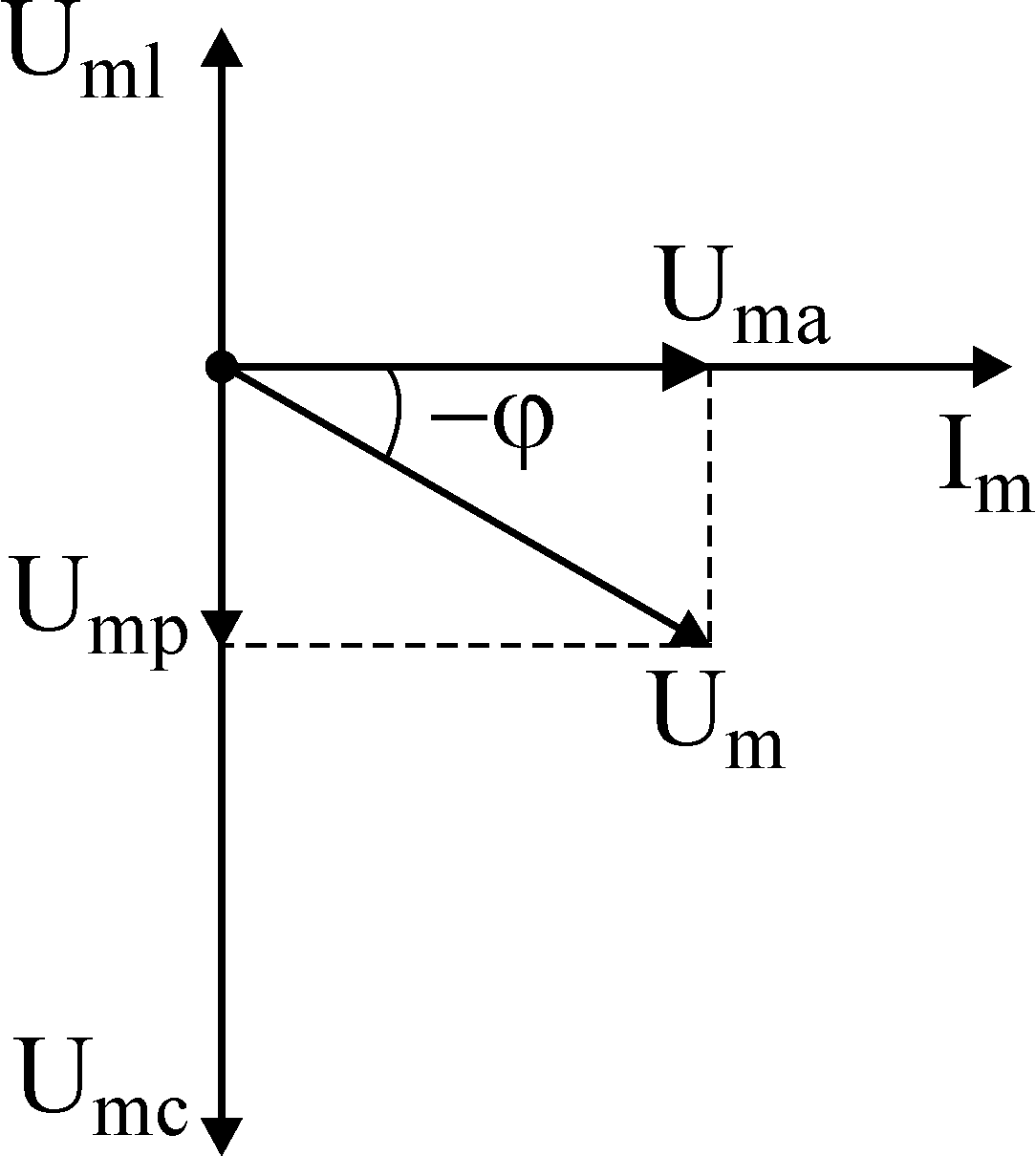
–цепь имеет емкостной характер.

Разделив все напряжения на ток, можно получить треугольник сопротивлений.

; .

Рассмотрим еще одну простую цепь – из параллельного соединенияR, L, C.

Допустим

,

.

По 1-му закону Кирхгофа:

где

–активная проводимость;

–индуктивная проводимость;

–емкостная проводимость;

–реактивная проводимость.

( b, как и Х имеет знак  в зависимости, что больше b_L или b_C).

Если изобразить расчет тока в цепи в виде векторов, то получи:

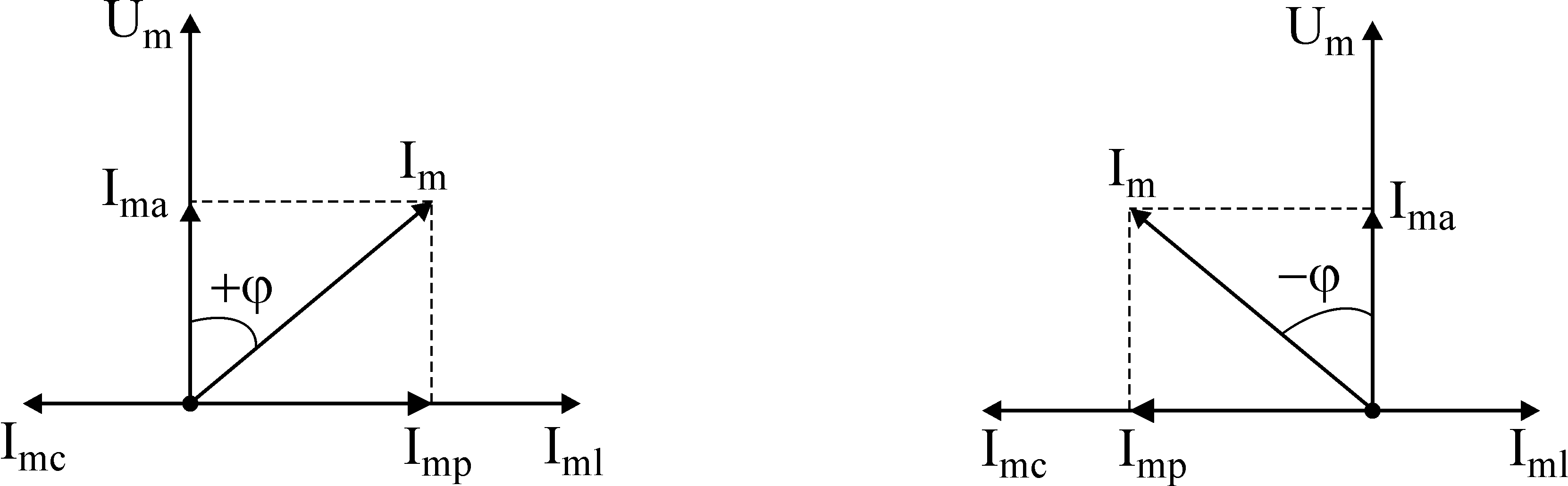
Разделив токи на напряжения, получим треугольник проводимостей.

;

Данный способ расчетов электрических цепей при периодических синусоидальных токах и напряжениях, когда приходится все время оперировать синусоидальными (косинусоидальными) функциями и понятиями полных сопротивлений и проводимостей и использовать при расчете векторные диаграммы по 1 и 2 законам Кирхгофа получил название графо-аналитического метода.

Большого применения, особенно при сложных цепях, этот метод не получил, ввиду большой сложности, особенно при ручном расчете.