Завдання №6 (варіант 1)

Відновлювана система телемеханіки має наступні результати вимірювань часу напрацювання на відмову:

№ відмов	1	2	3	4	5	6	7	8	9	10
tні(год.)	11	9,0	8,0	5,5	9,2	6,3	4,2	0,5	1,0	0,2

де t_ні(год.)– час роботи між сусідніми відмовами

Час поновлення є випадковою величиною, що приймається з ймовірністю Р_і значення t_П1 та Р₂ значення t_П2. Визначити коефіцієнт готовності системи.

Д ано:

Р₁=0,6 Коефіцієнт готовності визначаємо як відношення середнього

Р₂=0,2 часу наробітку безвідмовної роботи (Т_н) до суми Т_н+Т_п

t_п1=0,2

t_п2=2,0

t =10¹ (год) Час наробітку безвідмовної роботи визначається як:

К_г – ? (год)

Час поновлення визначаємо за формулою:

(год)

(год)

(год)

Відповідь : .

Завдання №7 (варіант 1)

Визначити ймовірність відмови системи телемеханіки за час t, якщо відомо, що час до відмови підпорядковується нормальному розподілу за часом Т.

Д ано: Ймовірність відмови комп’ютеризованої системи:

t=570(год) Q(t) = 1-P(t); P(t)=0.5- Φ(U);

T =490 (год) Отже, Q(t) = 0.5+Φ(U) ;

σ (t)=50

Q(t) – ?

Ймовірність відмови системи телемеханіки за час t:

Q(t) = 0.5+Φ(U) =0.5+0.44520=0.9452.

Відповідь: Ймовірність відмови системи телемеханіки за час t=570(год)=0.9452

Завдання №8 (варіант 2)

Поновлювана система телемеханіки має експоненційний закон розподілу часу наробітку на відмову і часу поновлення з параметрами λ та μ. Визначити основні показники надійності системи.

Д ано: Середній час до виникнення відмови:

λ =3*10^-2(1/год) Т_сер =1/λ=1/3·10^-2=33,3(год)

μ =1,5 (1/год) Час поновлення Т_п=1/μ=1/1,5=0,66(год)

К_г – ? Т_сер– ? Коефіцієнт готовності системи

D– ? σ– ? К_г= = =0,9805

Дисперсія часу до виникнення відмови:

D=1/λ²=1/(3·10^–2)²=3300 (год²)

Середньоквадратичне відхилення часу роботи:

σ =1/λ=1/3·10^–2=33,3 (год)

Відповідь: Т_сер=33,3(год); Т_п=0,66(год); К_г=0,9805; D=3300 (год²); σ =33,3(год)

Завдання №9 (варіант 2)

Визначити ймовірність Р_к(t) того, що за t годин роботи відбудеться k відмов у системі телемеханіки з інтенсивністю відмов λ.

Д ано:

λ=5·10^–4 (1/год) Ймовірність Р_к(t) того, що за t годин роботи виникне К

k=3 відмов в системі телемеханіки з інтенсивністю відмов λ,

t=30·10² (1/год) згідно з законом Пуассона:

Р _к(t)– ?

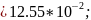
Відповідь: Р_к(t)=

Завдання №10 (варіант 2)

В системі телемеханіки використано гаряче дублювання елементів. Визначати середній час безвідмовної роботи і інтенсивність відмов для двох паралельно ввімкнутих по надійності елементів, якщо для кожного з них справедливий експоненційний закон з інтенсивністю відмов λ, а час роботи рівний t. Перемикач абсолютно надійний.

Д ано:

λ= 30·10^–6 (1/год) Структурна схема з’єднання елементів пристрою

t =40·10³ (год) λ

Т

λ(t)

_сер– ? =

λ (t) – ? λ

1) Знаходимо ймовірність безвідмовної роботи для даної системи. Так як елементи системи з’єднані паралельно, то:

.

Знаходимо середній час безвідмовної роботи:

(год);

Знаходимо інтенсивність відмов:

Відповідь: Т_сер= год.; λ(t)= .