1. Классическая линейная модель множественной регрессии (клммр). Оценивание неизвестных параметров: метод наименьших квадратов (мнк) и метод максимального правдоподобия (ммп).

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. Множественная регрессия применяется для исследования зависимости среднего значения анализируемых зависимых переменных от ряда независимых переменных или факторов.

Обозначим t-е наблюдение зависимой переменной Yt, а объясняющие переменные – xt1, xt2, …, xtp. Тогда модель множественной линейной регрессии можно представить в виде: Yt=1*q1(xt1)+ 2*q2(xt2)+…+ k*qk(xtk)+…+ p*qp(xtp)+ εt

Yt-эндогенная переменная

k (k=1,…p – число параметров) – параметр модели

Xtp (t=1,…,n – число наблюдений) – значение фактора Xp в наблюдении t (экзогенная переменная)

εt – случайная ошибка наблюдения.

qp( ) – некоторые детерминированные функции

Все параметры  - неизвестны и подлежат оцениванию.

Модель является линейной по параметрам и м.б. нелинейной по переменным

Рассмотрим следующую модель:

Yt=1*xt1+ 2*xt2+…+ k*xtk+…+ p*xtp+ εt

Для аналитического исследования введём обозначения:

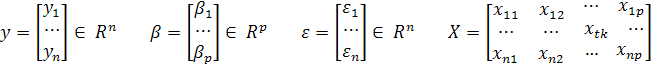
Модель м.б. представлена в виде: y=X+ε

Причины существования ε:

1. невозможно учесть все факторы (объясняющие переменные)

2. агрегирование переменных (объединение в одной переменной несколько)

3. ошибки измерения

4. ошибки выборки (неоднородность данных)

5. ошибки спецификации (вид зависимости)

Выбор формы зависимости между экзо- и эндогенными переменными имеет 3 способа

1. графический

2. аналитический

3. экспериментально

Основные гипотезы, лежащие в основе модели:

1. y=+ε – спецификация (линейная) уравнения регрессии

2. - матрица Х, детерминированная матрица max-го ранга k ( rang(X)=k ), k<n. Все столбцы матрицы линейно-независимы.

3. а) Е(ε)=0; т.е. Е( )-мат. ожидание

V(ε)=E(ε’ ε)= σ²In V( )-дисперсия In-единичная матрица

б) Cov(ε_t, ε_s)=0 Cov( )- ковариация. Отсутствие системной связи м-ду ошибками в разных наблюдениях. Если это условие не выполняется, то говорят об автокорреляции.

с) случайные ошибки д. иметь нормальное распределение с нулевым средним и постоянной дисперсией. εN(0; σ²In)

Множественная регрессия явл. обобщением парной регрессии и исп-ся для описания зависимости между зависимой переменой У и независимыми переменными Х₁,Х₂,…,Х_k. Множественная регрессия м. б. лин. и нелин., но распространение в эк-ке получила линейная множественная регрессия.

Выбор. регрессия:

Как и в парной регрессии случ-й член ε должен удовл-ть осн-м предположениям регресс-го анализа. Тогда с помощью МНК получ наилучшие оценки параметров теоретической регрессии. Кроме того переменные Х₁,Х₂,…,Х_k должны быть некоррелированы (линейно независимы) друг с другом. Для записи формул для оценки коэффициентов регрессии, полученные на основе МНК, введем следующие обозначения:

Тогда можно записать в векторно-матричной форме теоретическую модель: и выборочную регрессию . МНК приводит к формуле для оценки вектора α коэффициентов выборочной регрессии:

Для оценки коэффициентов множественной линейной регрессии с двумя независимыми переменными , можно решить систему уравнений: