Федеральное агентство по образованию гоу впо «тверской государственный технический университет»

­­­­­­­­­­­­­­­­­

Кафедра теплофизики

Р Е Ш Е Н И Е З А Д А Ч П О Ф И З И К Е

Часть 1 механика и молекулярная физика

Методические указания для заочников

Тверь 2010

Кинематика материальной точки

1. Путь , пройденный телом, это длина траектории, которая может быть задана в виде зависимости координат от времени

2. Скорость движения точки v характеризует ее перемещение за единицу времени и равна производной от пути по времени:

.

Проекции вектора скорости на оси ОХ и ОY могут быть найдены, как производные от соответствующих координат:

,

,

Модуль (абсолютную величину) скорости можно найти по формуле

3. Ускорение точки a характеризует изменение ее скорости за единицу времени и равно производной вектора скорости по времени:

.

Проекции вектора ускорения a_х и a_у и его модуль а равны

,

,

4. Для удобства анализа характера движения точки ускорение раскладывают на две составляющие:

− тангенциальное ускорение a_ характеризует изменение вектора скорости только по величине и равно производной модуля скорости по времени:

вектор a_ сонаправлен с вектором скорости v при ускоренном движении (а_ > 0)  и направлен противоположно v при замедленном (а_ < 0).

− нормальное ускорение a_n характеризует изменение вектора скорости только по направлению и связано с величиной скорости v и радиусом кривизны траектории r соотношением

;

вектор a_n нормален (перпендикулярен) вектору скорости v и направлен к центру кривизны траектории.

Поскольку векторы a_n и a_ взаимно перпендикулярны, для них справедливо выражение

Пример

Уравнение движения материальной точки имеет вид: , где A= 4 м/с, В =-0,05 м/с². Построить графики зависимостей x(t); v_x(t); a_x(t) . Для этого вычислить их значения в интервале времени от 0 до t₀ с шагом Δt, где t₀ =100 с, Δt=5 с.

Решение:

1) - проекция скорости на ось х равна первой производной от координаты x от времени;

;

2) м/с² - проекция ускорения на ось х равна производной от проекции скорости на ось х. Так как проекция ускорения не зависит от времени, движение является прямолинейным равноускоренным.

3) График зависимости координаты от времени.

t, c	0	5	10	15	20	25	30	35	40	45	50
x, м	0	18,75	35	48,75	60	68,75	75	78,75	80	78,75	75
t, c	55	60	65	70	75	80	85	90	95	100
x, м	68,75	60	48,75	35	18,75	0	-21,25	-45	-71,25	-100

Графики зависимости проекции скорости на ось x от времени:

;

(м/с)

t, c	0	5	10	15	20	25	30	35	40	45	50
v, м /c	4	3,5	3	2,5	2	1,5	1	0,5	0	-0,5	-1
t, c	55	60	65	70	75	80	85	90	95	100
v, м /c	-1,5	-2	-2,5	-3	-3,5	-4	-4,5	-5	-5,5	-6

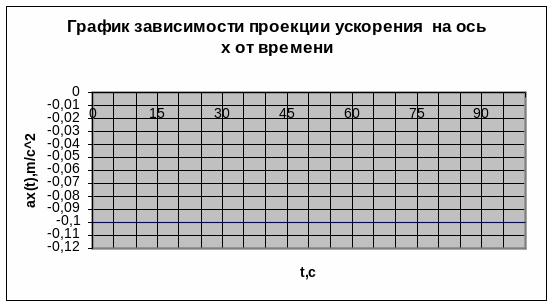
График зависимости проекции ускорения на ось x от времени:

а_x=-0,1 м/с²