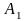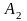Основная литература
Шипачёв, В.С. Высшая математика: учебник для вузов.- 8-е изд., стер.- М.: Высшая школа, 2007.- 479с., илл. ББК 22.1 МО
Башмаков, М.И. Математика. Сборник задач профильной направленности: учеб. пособие для СПО.- М.: Академия, 2012.- 208с. ББК 22.1 ФИРО
Башмаков, М.И. Математика. Задачник: учеб. пособие для СПО.- М.: Академия, 2012.- 416с. ББК 22.1 ФИРО
Федорова Н.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7227-3
Лукша В.В. Математика. Учебное пособие. – Волгоградский институт бизнеса, вузовское образование. 2013. ISBN: 978-5-9061-7228-0
Щербакова Ю.В. Аналитическая геометрия. Учебное пособие. Научная книга. 2012.
Березина Н.А. Линейная алгебра. Учебное пособие. Научная книга. 2012.
Дополнительная литература
Высшая математика для экономистов: Учебник / Кремер Н.Ш. - М.: Юнити, 2006, 2008, 2009.
Сборник задач по высшей математике для экономистов: Учб. пособ./ Под ред. В.И. Ермакова-М.:ИНФРА-М,2004.
Общий курс высшей математики (для экономистов): Учебник / Под ред. Ермакова В.И. – М.: Инфра-М, 2003.
Кузнецов Б. Т. Математика. М., ЮНИТИ, 2004
Формы текущего контроля знаний: решение задач.
Формы контроля самостоятельной работы студентов: ответы на вопросы, проверка решения задач, заданных на дом.
2. Варианты контрольных работ
Вариант 1
Задача 1. Найти общее и частное решения каждой системы.
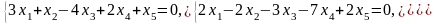
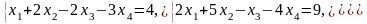
Задача 2. Найти
координаты вектора
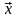в базисе
,
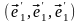если он задан в базисе
.
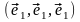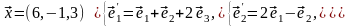
Задача 3. Для
пирамиды с вершинами в точках
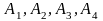найти:
а) длину ребра
;
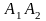б) угол между
ребрами
и
;
в) уравнение
плоскости
;
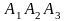г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение
высоты, опущенной из точки
на грань
;
ж) объем пирамиды
.
№ |
|
|
|
|
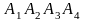1 |
(2,3,1) |
(4,1,-2) |
(6,3,7) |
(-5,-4,8) |
Вариант 2
Задача 1. Найти общее и частное решения каждой системы.
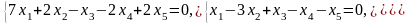
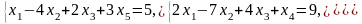
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
2 |
(4,2,5) |
(0,7,2) |
(0,2,7) |
(1,5,0) |
Вариант 3
Задача 1. Найти общее и частное решения каждой системы.
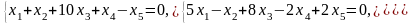
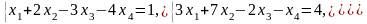
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
3 |
(4,4,10) |
(4,0,2) |
(2,8,4) |
(9,6,4) |
Вариант 4
Задача 1. Найти общее и частное решения каждой системы.
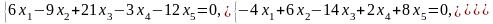
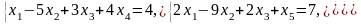
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
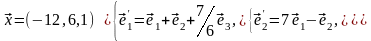
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
4 |
(2,2,2) |
(2,4,1) |
(-1,2,3) |
(3,6,1) |
Вариант 5
Задача 1. Найти общее и частное решения каждой системы.
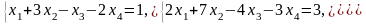
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
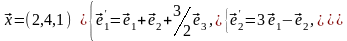
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
5 |
(1,3,0) |
(4,-1,2) |
(3,0,1) |
(-4,3,5) |
Вариант 6
Задача 1. Найти общее и частное решения каждой системы.
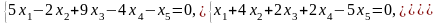
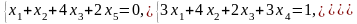
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
6 |
(-2,0,-4) |
(-1,7,1) |
(4,-8,-4) |
(1,-4,6) |
Вариант 7
Задача 1. Найти общее и частное решения каждой системы.
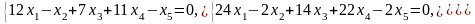
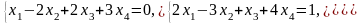
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
7 |
(5,2,0) |
(2,5,0) |
(1,2,4) |
(-1,1,1) |
Вариант 8
Задача 1. Найти общее и частное решения каждой системы.
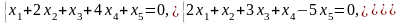
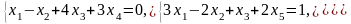
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
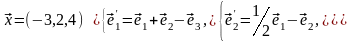
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
8 |
(2,-1,2) |
(1,2,-1) |
(3,2,1) |
(-4,2,5) |
Вариант 9
Задача 1. Найти общее и частное решения каждой системы.
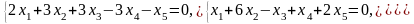
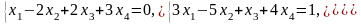
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
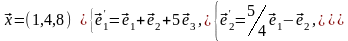
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
9 |
(1,1,2) |
(-1,1,3) |
(2,-2,4) |
(-1,0,-2) |
Вариант 10
Задача 1. Найти общее и частное решения каждой системы.
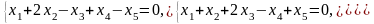
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
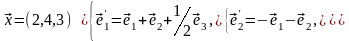
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
10 |
(4,-1,4) |
(4,-3,6) |
(3,-1,3) |
(4,-2,3) |
Вариант 11
Задача 1. Найти общее и частное решения каждой системы.
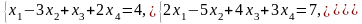
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
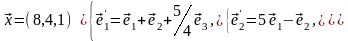
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
11 |
(3,5,-1) |
(5,3,-4) |
(7,5,5) |
(-4,-2,6) |
Вариант 12
Задача 1. Найти общее и частное решения каждой системы.
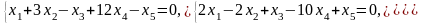
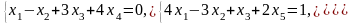
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
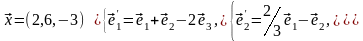
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
12 |
(6,3,6) |
(2,8,3) |
(2,3,8) |
(3,6,1) |
Вариант 13
Задача 1. Найти общее и частное решения каждой системы.
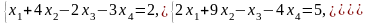
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
13 |
(3,2,7) |
(3,-2,-1) |
(1,6,1) |
(8,4,1) |
Вариант 14
Задача 1. Найти общее и частное решения каждой системы.
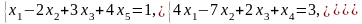
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
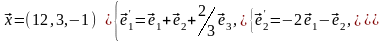
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
14 |
(3,4,3) |
(3,6,2) |
(0,4,4) |
(4,8,2) |
Вариант 15
Задача 1. Найти общее и частное решения каждой системы.
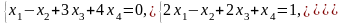
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
15 |
(2,5,-1) |
(5,1,1) |
(4,2,0) |
(-3,5,4) |
Вариант 16
Задача 1. Найти общее и частное решения каждой системы.
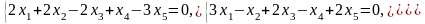
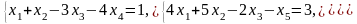
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
16 |
(-4,1,-3) |
(-3,8,2) |
(2,-7,-3) |
(-1,-3,7) |
Вариант 17
Задача 1. Найти общее и частное решения каждой системы.
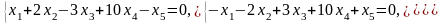
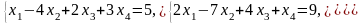
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
17 |
(4,3,2) |
(1,6,2) |
(0,3,6) |
(-2,2,3) |
Вариант 18
Задача 1. Найти общее и частное решения каждой системы.
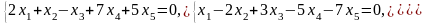
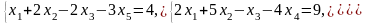
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
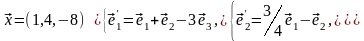
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
18 |
(4,2,5) |
(3,5,2) |
(5,5,4) |
(-2,5,8) |
Вариант 19
Задача 1. Найти общее и частное решения каждой системы.
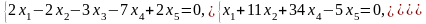
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
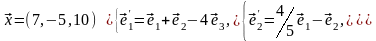
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
19 |
(3,2,2) |
(1,2,3) |
(4,-1,4) |
(1,1,-2) |
Вариант 20
Задача 1. Найти общее и частное решения каждой системы.
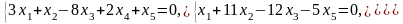
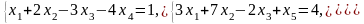
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
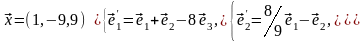
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
20 |
(3,1,2) |
(3,-1,4) |
(2,1,1) |
(3,0,1) |
Вариант 21
Задача 1. Найти общее и частное решения каждой системы.
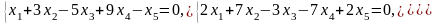
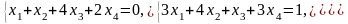
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
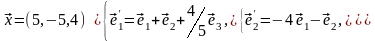
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
21 |
(-1,6,2) |
(1,4,-1) |
(3,6,8) |
(-8,-1,9) |
Вариант 22
Задача 1. Найти общее и частное решения каждой системы.
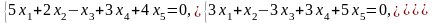
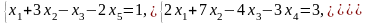
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
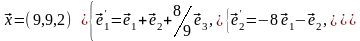
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
22 |
(2,1,4) |
(-2,6,1) |
(-2,1,6) |
(-1,4,-1) |
Вариант 23
Задача 1. Найти общее и частное решения каждой системы.
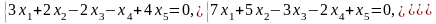
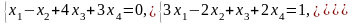
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
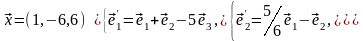
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
23 |
(1,3,5) |
(1,-1,-3) |
(-1,7,-1) |
(6,5,-1) |
Вариант 24
Задача 1. Найти общее и частное решения каждой системы.
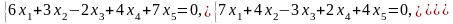
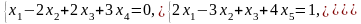
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
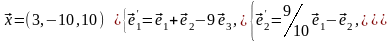
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
24 |
(2,3,0) |
(2,5,-1) |
(-1,3,1) |
(3,7,-1) |
Вариант 25
Задача 1. Найти общее и частное решения каждой системы.
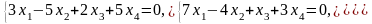
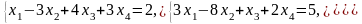
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
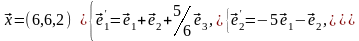
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
25 |
(3,7,-2) |
(6,3,0) |
(5,4,-1) |
(-2,7,3) |
Вариант 26
Задача 1. Найти общее и частное решения каждой системы.
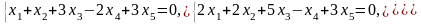
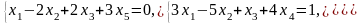
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
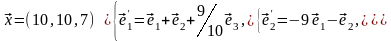
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
26 |
(-2,2,-2) |
(-1,9,3) |
(4,-6,-2) |
(1,-2,8) |
Вариант 27
Задача 1. Найти общее и частное решения каждой системы.
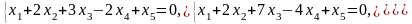
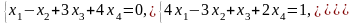
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
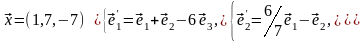
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
27 |
(6,1,3) |
(3,4,3) |
(2,1,7) |
(0,0,4) |
Вариант 28
Задача 1. Найти общее и частное решения каждой системы.
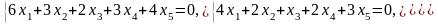
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
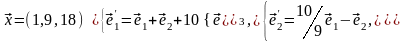
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
28 |
(5,1,4) |
(4,4,1) |
(6,4,3) |
(-1,4,7) |
Вариант 29
Задача 1. Найти общее и частное решения каждой системы.
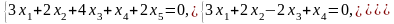
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
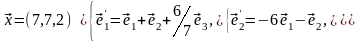
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
29 |
(4,4,3) |
(2,4,4) |
(5,1,5) |
(2,3,-1) |
Вариант 30
Задача 1. Найти общее и частное решения каждой системы.
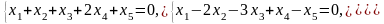
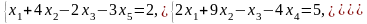
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
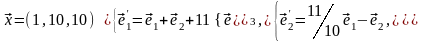
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
30 |
(2,3,3) |
(2,1,5) |
(1,3,2) |
(2,2,2) |
Вариант 31
Задача 1. Найти общее и частное решения каждой системы.
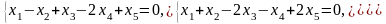
Задача 2. Найти координаты вектора в базисе , если он задан в базисе .
Задача 3. Для пирамиды с вершинами в точках найти:
а) длину ребра ;
б) угол между ребрами и ;
в) уравнение плоскости ;
г) площадь грани ;
д) угол между ребром и плоскостью ;
е) уравнение высоты, опущенной из точки на грань ;
ж) объем пирамиды .
№ |
|
|
|
|
31 |
(6,5,2) |
(4,5,3) |
(7,2,4) |
(4,4,-2) |