5.3 Критерій згоди Колмогорова

1. Висуваємо гіпотезу 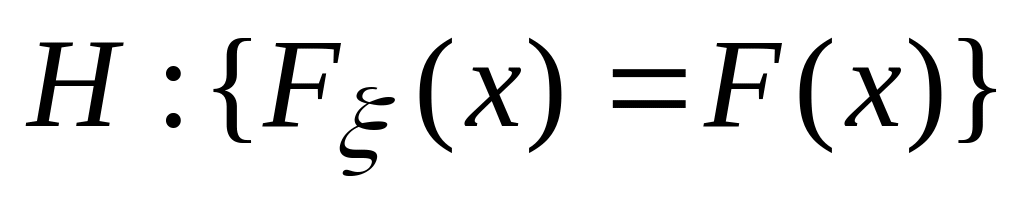відносно закону розподілу випадкової величини і вважаємо, що функція 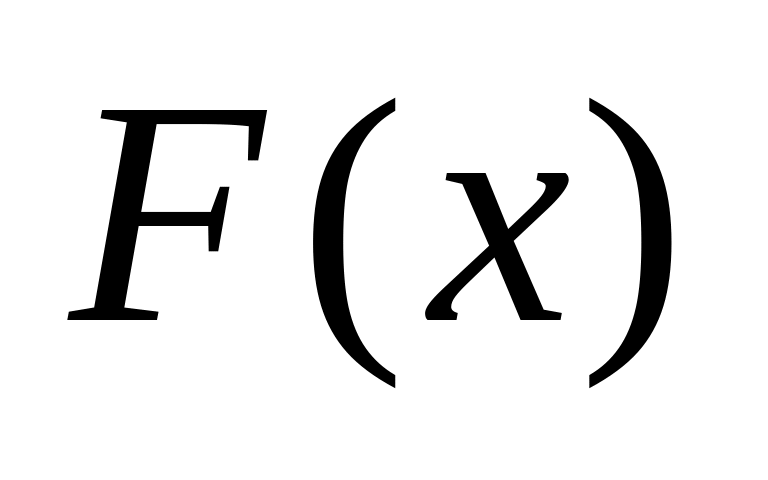задана і неперервна.

2. Задаємо рівень значущості .

3. За міру відхилення емпіричної функції розподілу 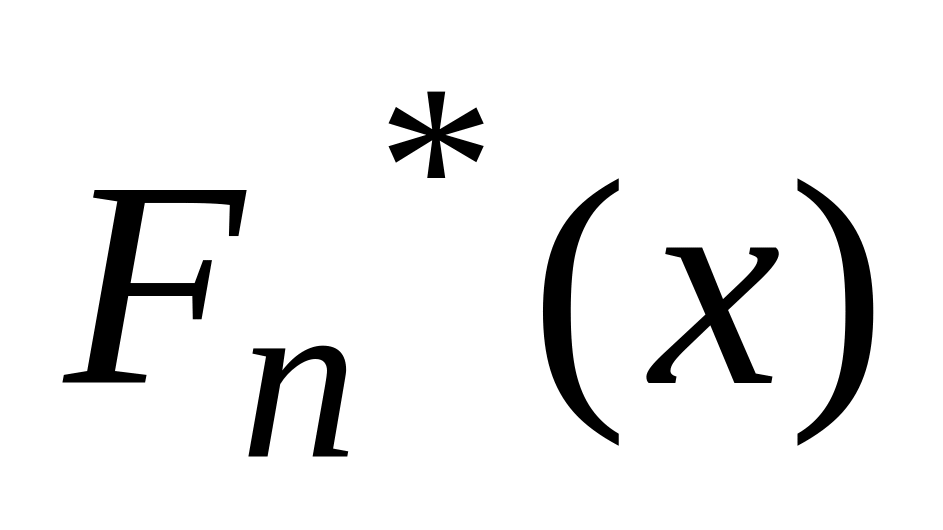у вибірки 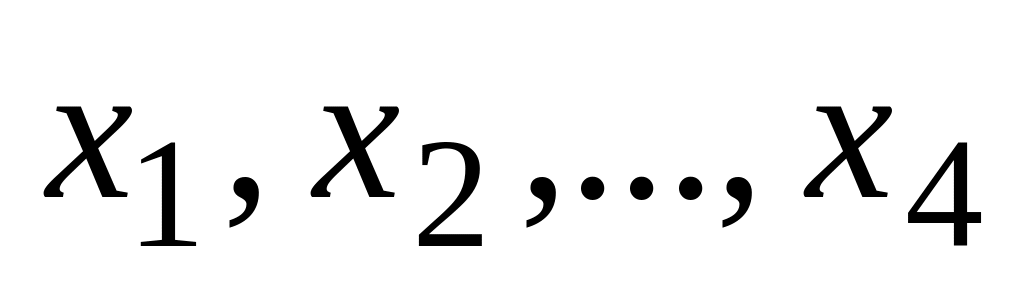від гіпотетичної функції розподілу Колмогоров запропонував взяти величину

,

де - точна верхня грань множини значень по усіх можливих значеннях .

4. Знаходимо 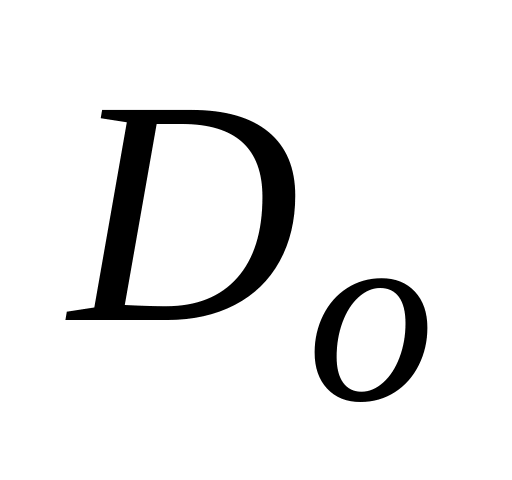таке, що і розглянемо рівняння 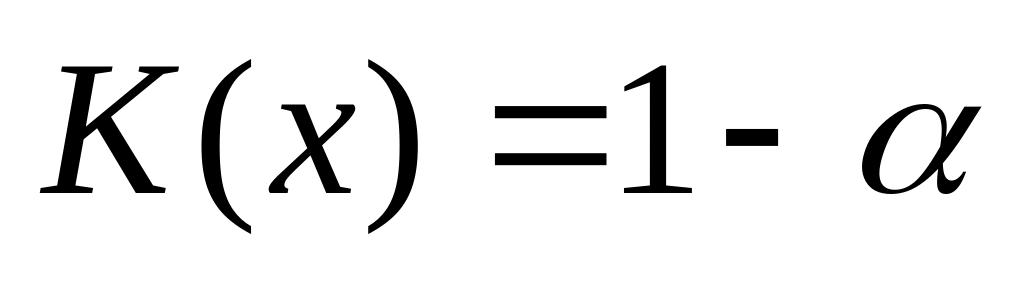. За таблицею функції Колмогорова (таблиця №12 додатку 2) знаходимо корінь 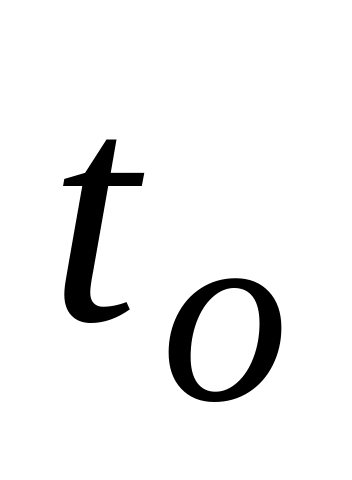цього рівняння.

Тоді із теореми Колмогорова маємо

. Звідси .

5. За вибіркою визначаємо величину .

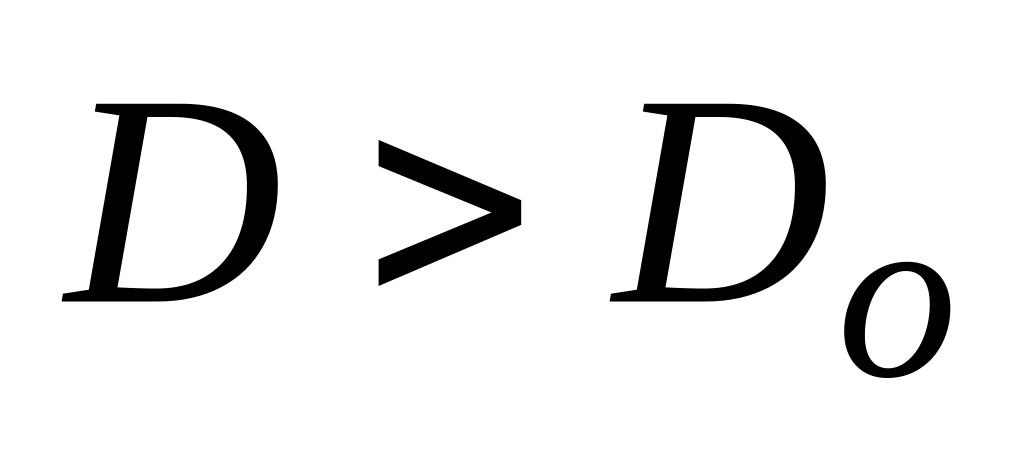6. Якщо , гіпотезу відхиляємо,

якщо гупотезу приймаємо.

Зауваження 1

При великих ( ) використовують асимптотичний розподіл Колмогорова :

.

Зауваження 2

Критерій А. М. Колмогорова застосовується тоді, коли гіпотетичний розподіл цілком визначений. Якщо ж гіпотетичний розподіл залежить від параметрів, які ми оцінюємо за вибіркою, критерій Колмогорова не використовують.

Сформулюємо практичне правило.

При заданому рівні значущості перевірку за критерієм Колмогорова нульової гіпотези : вибірку взято з генеральної сукупності з функцією розподілу , проводять за схемою :

1. За вибіркою будують емпіричну функцію розподілу .

Обчислюють значення - гіпотетичної теоретичної функції розподілу і значення - емпіричної функції розподілу .

Знаходять максимум модуля різниці між ними

,

і спостережуване значення критерію

.

Зауваження 3.

Всі обчислення на даному етапі зручно проводити за допомогою розрахункової таблиці виду :

Таблиця 1.

1	2	3	4	5

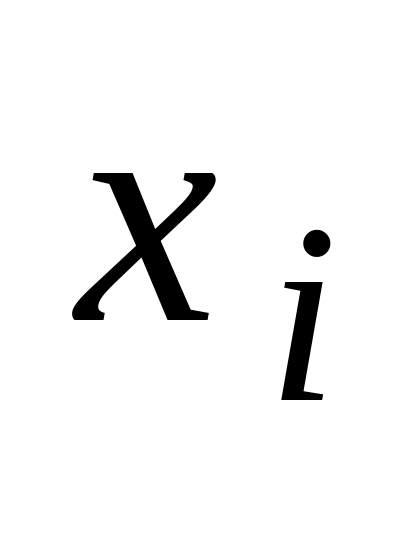
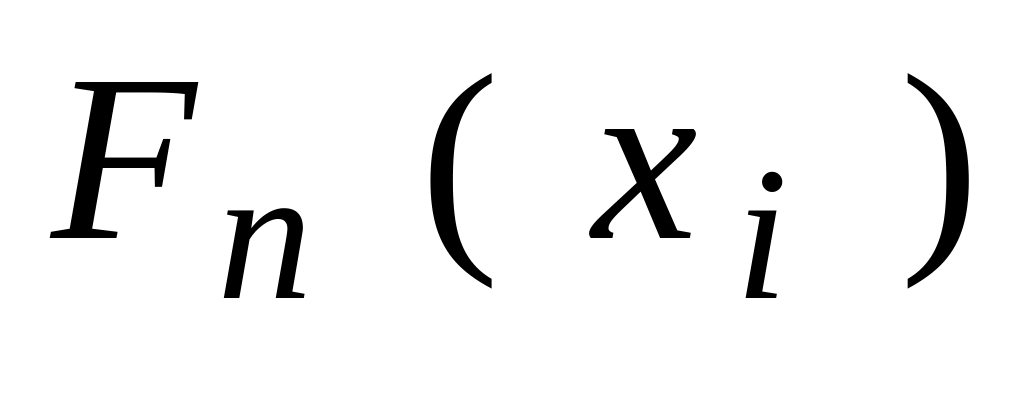
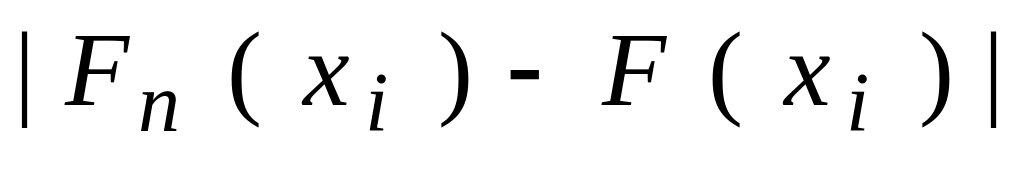
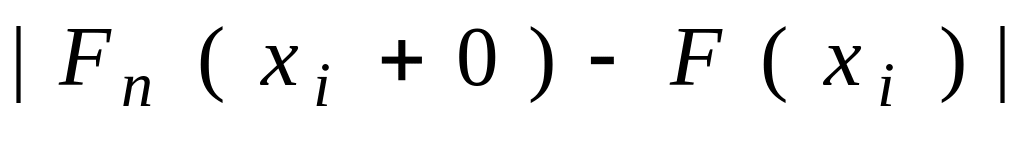
Оскільки емпірична функція розподілу має в точках розриви I роду, то для визначення максимального відхилення в розрахункову таблицю вводиться останній стовбець.

З останніх двох стовпців знаходять максимальне значення і обчислюють спостережуване значення критерію

.

2. За рівнем значущості і об’ємом вибірки з таблиці критичних значень розподілу А. М. Колмогорова (таблиця № 12 додатку 2) знаходять критичну точку критичної області .

Якщо - нульову гіпотезу приймають.

Якщо - нульову гіпотезу відхиляють.

Приклад 5.2

Дано вибірку 25 незалежних спостережень над неперервною випадковою змінною

-1,5	4,8	2,0	8,7	4,9
-10,4	-10,3	2,4	9,4	7,1
7,7	7,8	15,0	11,0	17,5
13,8	19,3	4,4	-3,1	-5,2
-3,6	12,7	3,3	21,8	-6,7

При рівні значущості перевірити гіпотезу

: вибірку взято з нормально розподіленої генеральної сукупності з параметрами , тобто .

 Якщо гіпотеза вірна, то лінійно перетворена вибірка за формулою буде нормально розподілена з параметрами , , тобто .

Лінійно перетворена вибірка така :

-0,65	-0,02	-0,30	0,37	-0,01
-1,54	-1,53	-0,26	0,44	0,21
0,27	0,28	1,00	0,60	1,25
0,88	1,43	-0,06	-0,51	-1,21
-0,86	0,77	-0,17	1,68	-1,17

Запишемо варіантний ряд для , значення емпіричної і гіпотетичної функції розподілу в точках варіантного ряду і обчислимо різниці абсолютних відхилень.

Значення - гіпотетичної функції розподілу знаходимо за таблицею значень нормальної функції розподілу (таблиця № 15 додатку 2).

Заповнюємо розрахункову таблицю 1.

З останніх двох стовпців знаходимо максимальне значення відхилення 0.1021.

Тоді .

З таблиці критичних значень розподілу А. М. Колмогорова (таблиця № 12 додатку 2) знаходимо критичну точку критичної області =1,36.

Оскільки - нульову гіпотезу приймаємо.