5.Примеры решения задач.

Пример 12.1. Найдём массу части плоскости 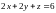, ограниченной координатными плоскостями, если плотность в каждой точке .

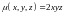Решение. Построим заданную часть плоскости ( см. рис. 12.1). .

Поверхность G однозначно проецируется на координатную плоскость XOY, поэтому для вычисления массы (12.5) применим формулу (12.1).

Рисунок 5.1

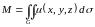
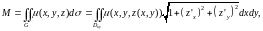где , .

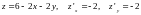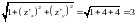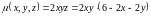
Подставляем всё в подынтегральное выражение и вычисляем интеграл.

.

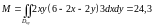Ответ: .

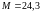Пример 12.2. Вычислим координаты центра масс части поверхности полусферы 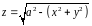, вырезанной цилиндром 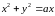, если плотность .

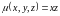Р ешение. Построим заданные поверхности и выделим нужную часть полусферы (на рис. 12.2 она выделена синим цветом). Поверхность удобно проецируется на плоскость в область, ограниченную окружностью .

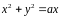И

Рисунок 12.2

спользуя формулы (12.5) и (12.1) составим интеграл для вычисления массы части поверхности.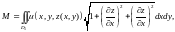

где .

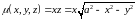
Вычислим частные производные.

.

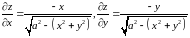
Упростим подкоренное выражение и получим интеграл

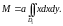
Выберем способ его вычисления. В данном случае удобнее перейти к полярным координатам и учесть симметрию относительно оси .

Составим повторный интеграл и вычислим его:

.

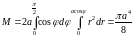Далее, по формулам (12.6) вычисляем координаты центра масс. С учётом симметрии поверхности и функции плотности, без вычисления определяем, что ордината центра масс равна нулю. Для двух других координат составляем интегралы и вычисляем их.

.

.

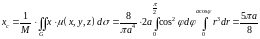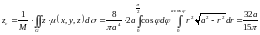Ответ: С .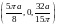

Занятие 13. Понятие гладкой и кусочно-гладкой поверхности. Ориентированные поверхности и их ориентация. Нормаль к поверхности. Определение поверхностного интеграла второго рода, его свойства. Вычисление поверхностного интеграла второго рода с помощью двойного ин-теграла. Физический смысл поверхностного интеграла второго рода. ОЛ-1гл.6, ОЛ-2 гл.3, ОЛ-4 § 12.

Практика: ОЛ-6 №№ 2350, 2351 (№ 2351 решить двумя способами: 1) с помощью вычисления составных интегралов, 2) сведением к поверхностному интегралу 1-го рода) или: ОЛ-5 №№ 10.84, 85, 87, 94.

Домашнее задание к занятию 13:

ОЛ-6 № 2349 (решить двумя способами) или ОЛ-5 №№ 10.83, 86, 88.

1.Понятие гладкой поверхности. Ориентированная поверхность.

Определение. Поверхность называется гладкой, если в каждой её точке существует касательная плоскость, непрерывно меняющаяся вдоль поверхности.

Если поверхность состоит из нескольких гладких частей, примыкающих друг к другу и не имеющих общих внутренних точек, то она называется кусочно-гладкой.

В каждой точке гладкой поверхности можно построить единичный нормальный вектор 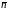, который непрерывно будет перемещаться вместе с перемещающейся касательной плоскостью.

В

Рисунок 13.6

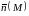озьмём на гладкой поверхности произвольную точку и зафиксируем нормальный вектор . Если при движении этой точки по какому-либо контуру, принадлежащему поверхности и не пересекающему её границы, точка может прийти в исходное положение так, что при этом нормальный вектор окажется противоположно направленным своему первоначальному положению, то эта поверхность называется односторонней.

П

Рисунок 13.7

римером односторонней поверхности является «лист Мёбиуса» (см. рис. 13.1).

Если такая ситуация невозможна, поверхность называется двусторонней.

Определение. Двусторонняя гладкая поверхность называется ориентированной, если в некоторой её точке выбран один из двух возможных нормальный вектор так, чтобы он непрерывно менялся от точки к точке (см. рис. 13.2).