
- •Б.Т. Добрица, и.В. Дубограй, о.В. Скуднева. Криволинейные, поверхностные интегралы и элементы теории поля.
- •1.Определение криволинейного интеграла 1-ого рода.
- •2.Свойства криволинейного интеграла 1 рода.
- •3.Способы вычисления криволинейного интеграла 1 рода.
- •4.Теорема существования криволинейного интеграла 1 рода.
- •5.Физические приложения криволинейного интеграла первого рода.
- •6.Примеры решения задач.
- •1.Определение криволинейного интеграла второго рода.
- •2.Теорема существования криволинейного интеграла 2-ого рода.
- •4.Вычисление криволинейного интеграла 2-ого рода.
- •5. Работа силы при перемещении материальной точки единичной массы из точки в точку вдоль кривой .
- •1.Формула Грина.
- •2. Независимость криволинейного интеграла от пути интегрирования.
- •Определение поверхностного интеграла первого рода.
- •2.Вычисление поверхностного интеграла 1-ого рода.
- •5.Примеры решения задач.
- •1.Понятие гладкой поверхности. Ориентированная поверхность.
- •2.Определение поверхностного интеграла второго рода.
- •3.Вычисление поверхностного интеграла 2-ого рода.
- •1.Векторное поле.
- •2. Векторные линии поля.
- •3.Поток векторного поля через поверхность.
- •4.Дивергенция векторного поля. Соленоидальное векторное поле.
- •Формула Остроградского – Гаусса.
- •1.Криволинейный интеграл в векторном поле.
- •2. Потенциальное векторное поле.
- •4. Ротор (вихрь) векторного поля. Формула Стокса.
- •1.Оператор Гамильтона.
- •2.Дифференциальные операции первого порядка.
- •2.Дифференциальные операции второго порядка.
- •4.Запись дифференциальных операций второго порядка в операторной форме.
2. Независимость криволинейного интеграла от пути интегрирования.
Пусть
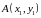 и
и
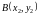 -
произвольные точки односвязной области
пл.
-
произвольные точки односвязной области
пл.
 .
Криволинейные интегралы, вычисленные
по различным кривым, соединяющим эти
точки, в общем случае имеют различные
значения. Но при выполнении некоторых
условий все эти значения могут оказаться
одинаковыми. Тогда интеграл не зависит
от формы пути, а зависит только от
начальной и конечной точек.
.
Криволинейные интегралы, вычисленные
по различным кривым, соединяющим эти
точки, в общем случае имеют различные
значения. Но при выполнении некоторых
условий все эти значения могут оказаться
одинаковыми. Тогда интеграл не зависит
от формы пути, а зависит только от
начальной и конечной точек.
Имеют место следующие теоремы.
Теорема
1. Для того,
чтобы интеграл
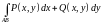 не зависел от формы пути, соединяющего
точки
и
,
необходимо и достаточно, чтобы этот
интеграл по любому замкнутому контуру
был равен нулю.
не зависел от формы пути, соединяющего
точки
и
,
необходимо и достаточно, чтобы этот
интеграл по любому замкнутому контуру
был равен нулю.
Теорема 2.
. Для того, чтобы интеграл
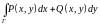 по любому замкнутому контуру был равен
нулю, необходимо и достаточно, чтобы
функции
и их частные производные
по любому замкнутому контуру был равен
нулю, необходимо и достаточно, чтобы
функции
и их частные производные
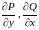 были непрерывны в замкнутой области
Г
и чтобы
выполнялось условие
были непрерывны в замкнутой области
Г
и чтобы
выполнялось условие
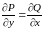 (11.2)
(11.2)
Таким
образом, если выполняются условия
независимости интеграла от формы пути
(11.2),
то достаточно указать только начальную
и конечную точки:
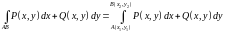 (11.3)
(11.3)
Теорема
3. Если
в односвязной области
выполняется
условие
,
то существует функция
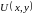 такая, что
такая, что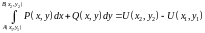 . (11.4)
. (11.4)
Эта формула называется формулой Ньютона – Лейбница для криволинейного интеграла.
Замечание.
Напомним,
что равенство
является необходимым и достаточным
условием того, что выражение
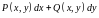 является полным дифференциалом некоторой
функции
.
является полным дифференциалом некоторой
функции
.
Тогда
из выше сформулированных теорем следует,
что если функции
и их частные производные
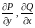 непрерывны в замкнутой области
Г
, в которой
даны точки
непрерывны в замкнутой области
Г
, в которой
даны точки
 и
и
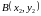 ,
и
,
то
,
и
,
то
а)
существует функция
,
такая, что
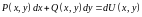 ,
,
б)
криволинейный интеграл от полного
дифференциала некоторой функции
не зависит от формы пути,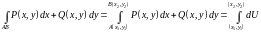 ,
,
в)
имеет место формула Ньютона
– Лейбница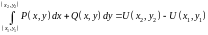 .
.
Пример
11.2. Убедимся
в том, что интеграл
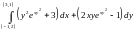 не зависит от формы пути, и вычислим
его.
не зависит от формы пути, и вычислим
его.
Решение.
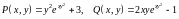 .
.
П
Рисунок 11.3
 роверим
выполнение условия (11.2)
.
роверим
выполнение условия (11.2)
.
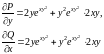 .
Как видим, условие выполнено. Значение
интеграла не зависит от пути интегрирования.
Выберем путь интегрирования. Наиболее
.
Как видим, условие выполнено. Значение
интеграла не зависит от пути интегрирования.
Выберем путь интегрирования. Наиболее
простым путём для вычислений является ломаная линия АСВ, соединяющая точки начала и конца пути. ( См. рис. 11.3)
Тогда
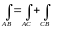 .
.
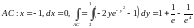
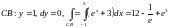
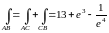
3. Нахождение функции по её полному дифференциалу.
С помощью криволинейного интеграла, который не зависит от формы пути, можно найти функцию , зная её полный дифференциал. Эта задача решается следующим образом.
 Если
функции
и их частные производные
непрерывны в замкнутой области
Г
и
Если
функции
и их частные производные
непрерывны в замкнутой области
Г
и
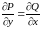 ,
то выражение
,
то выражение
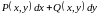 является полным дифференциалом некоторой
функции
.
Кроме этого интеграл
является полным дифференциалом некоторой
функции
.
Кроме этого интеграл
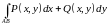 ,
во-первых, не зависит от формы пути и,
во-вторых, может быть вычислен по формуле
Ньютона – Лейбница.
,
во-первых, не зависит от формы пути и,
во-вторых, может быть вычислен по формуле
Ньютона – Лейбница.
Вычислим двумя способами.
а
Рисунок 11.4
) Выберем в области точку с конкретными координатами и точку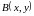 с произвольными координатами. Вычислим
криволинейный интеграл по ломаной,
состоящей из двух отрезков прямых,
соединяющих эти точки, причём один из
отрезков параллелен оси
,
а другой – оси
.
Тогда
с произвольными координатами. Вычислим
криволинейный интеграл по ломаной,
состоящей из двух отрезков прямых,
соединяющих эти точки, причём один из
отрезков параллелен оси
,
а другой – оси
.
Тогда
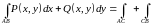 .
(См. рис. 11.4)
.
(См. рис. 11.4)
Уравнение
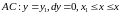 .
.
Уравнение
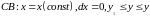 .
.
Получаем: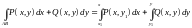 Вычислив оба интеграла, получаем в
ответе некоторую функцию
Вычислив оба интеграла, получаем в
ответе некоторую функцию
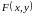 .
.
б) Теперь тот же интеграл вычислим по формуле Ньютона – Лейбница.
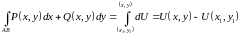 .
.
Теперь
сравним два результата вычисления
одного и того же интеграла. Функциональная
часть
ответа в пункте а) является искомой
функцией
,
а числовая часть – её значением в точке
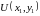 .
.
Пример 11.3. Убедимся
в том, что выражение
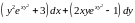 является полным дифференциалом некоторой
функции
и найдём её. Проверим результаты
вычисления примера 11.2 по формуле
Ньютона-Лейбница.
является полным дифференциалом некоторой
функции
и найдём её. Проверим результаты
вычисления примера 11.2 по формуле
Ньютона-Лейбница.
Решение.
Условие существования функции
(11.2)
было
проверено в предыдущем примере. Найдём
эту функцию, для чего воспользуемся
рисунком 11.4, причём примем за
точку
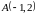 .
Составим и вычислим интеграл по ломаной
АСВ, где
.
Составим и вычислим интеграл по ломаной
АСВ, где
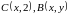 :
:
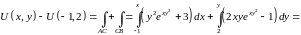
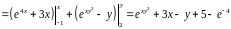 .
.
Как было сказано
выше, функциональная часть полученного
выражения и есть искомая функция
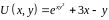 .
.
Проверим результат вычислений из примера 11.2 по формуле Ньютона –Лейбница:
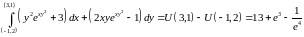 .
.
Результаты совпали.
Замечание. Все рассмотренные утверждения верны и для пространственного случая, но с большим количеством условий.
Пусть
кусочно-гладкая кривая
принадлежит области
в пространстве
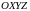 .
Тогда, если функции
.
Тогда, если функции
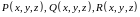 и их частные производные непрерывны
в замкнутой области
и их частные производные непрерывны
в замкнутой области
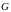 ,
в которой даны точки
,
в которой даны точки
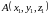 и
и
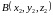 ,
и
,
и
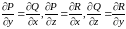 (11.5),
то
(11.5),
то
а)
выражение
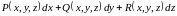 является
полным дифференциалом некоторой функции
является
полным дифференциалом некоторой функции
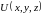 ,
,
б)
криволинейный интеграл от полного
дифференциала некоторой функции
не зависит от формы пути и
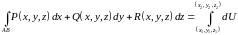 ,
,
в)
имеет место формула Ньютона
– Лейбница
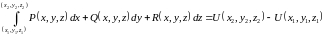 .(11.6)
.(11.6)
Пример 11.4.
Убедимся в том, что выражение
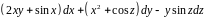 является полным дифференциалом некоторой
функции
и найдём её.
является полным дифференциалом некоторой
функции
и найдём её.
Решение.
Для ответа на вопрос о том, является ли
данное выражение полным дифференциалом
некоторой функции
,
вычислим частные производные от функций
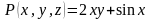 ,
,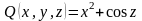 ,
,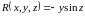 .
(См. (11.5))
.
(См. (11.5))
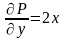 ;
;
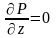 ;
;
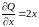 ;
;
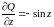 ;
;
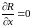 ;
;
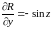 .
.
Эти функции непрерывны вместе со своими частными производными в любой точке пространства .
Видим,
что выполняются необходимые и достаточные
условия существования
:
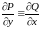 ,
,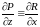 ,
,
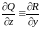 ,
ч. т. д.
,
ч. т. д.
Т.е.
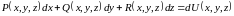 .
.
Для вычисления
функции
воспользуемся тем, что линейный интеграл
не зависит от пути интегрирования и
может быть вычислен по формуле
Ньютона-Лейбница. Пусть точка
 - начало пути, а некоторая точка
- начало пути, а некоторая точка
 - конец пути.
Вычислим
интеграл
- конец пути.
Вычислим
интеграл
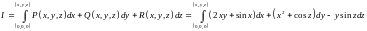
 по контуру,
состоящему из отрезков прямых, параллельных
координатным осям. (см.рис.11.5 Рисунок 12).
по контуру,
состоящему из отрезков прямых, параллельных
координатным осям. (см.рис.11.5 Рисунок 12).
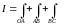 .
.
У
Рисунок 11.5
равнения частей контура: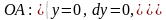 ,
,
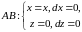 ,
,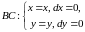 .
.
Тогда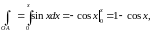
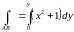 ,
x
здесь
зафиксирован, поэтому
,
x
здесь
зафиксирован, поэтому
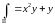 ,
,
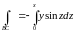 ,
здесь зафиксирован y,
поэтому
,
здесь зафиксирован y,
поэтому
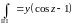 .
.
В итоге получаем: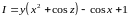 .
.
Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница.
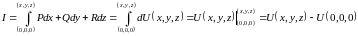
Приравняем
результаты: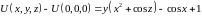 .
.
Из полученного
равенства следует, что
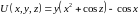 ,
а
,
а
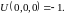
Ответ:
 .
.
Занятие 12.
Поверхностный интеграл первого рода: определение, основные свойства. Правила вычисления поверхностного интеграла первого рода с помощью двойного интеграла. Приложения поверхностного интеграла первого рода: площадь поверхности, масса материальной поверхности, статические моменты относительно координатных плоскостей, моменты инерции и координаты центра тяжести. ОЛ-1 гл.6, ОЛ 2 гл.3, ОЛ-4 § 11.
Практика: ОЛ-6 №№ 2347, 2352, 2353 или ОЛ-5 №№ 10.62, 65, 67.
Домашнее задание к занятию 12:
ОЛ-6 №№ 2348, 2354 или ОЛ-5 №№ 10.63, 64, 68.
