1.Определение криволинейного интеграла второго рода.

Рисунок 10.1

ок 9. 4

Рассмотрим кусочно-гладкую кривую , в каждой точке М которой задана функция 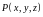. Разобьём эту кривую на малых частей точками так, чтобы в точках каждой части значение функции 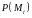можно было считать постоянным, а сама часть могла быть принята за отрезок прямой (см. рис. 10.1). Пусть 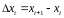- проекция i-ой части разбиения на ось . На каждой части выберем произвольную точку и составим интегральную сумму . Определение. Криволинейным интегралом второго рода по переменной называется предел последовательности интегральных сумм (если он существует) при неограниченном увеличении числа разбиений и стремлении длины каждой части к нулю. Такой интеграл обозначается следующим образом: 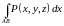. 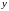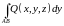По аналогии можно определить интегралы по переменным и : и 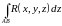. И тогда можно рассматривать криволинейный интеграл второго рода общего вида 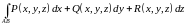(10.1)

2.Теорема существования криволинейного интеграла 2-ого рода.

Если функция 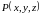непрерывна в каждой точке кусочно - гладкой кривой, то она интегрируема по этой кривой по переменной , т.е. существует предел последовательности интегральных сумм и он не зависит от способа разбиения кривой на части и выбора промежуточных точек. 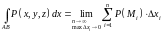. (10.2) 3. Основные свойства криволинейного интеграла 2-ого рода.

1.Линейность. Криволинейный интеграл 2-ого рода от линейной комбинации интегрируемых по кривой функций равен линейной комбинации интегралов от этих функций. В частности, 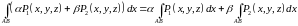. 2.Аддитивность. Если кривая 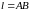разбита на две части, не имеющие общих внутренних точек, то .

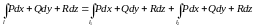3.Изменение знака при изменении направления движения по кривой. 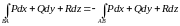. Это свойство отличается от аналогичного свойства для ранее рассмотренных интегралов. Появление минуса связано с тем, что в соответствующей интегральной сумме при изменении направления перемещения точки по кривой изменит свой знак . А следовательно, изменит знак и интеграл (см. (10.2)).

4.Вычисление криволинейного интеграла 2-ого рода.

Криволинейный интеграл 2-ого рода вычисляется так же, как криволинейный интеграл 1-ого рода сведением к определённому. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование.

а) Если линия АВ задана системой уравнений то

(10.3)

Для плоского случая, когда кривая задана уравнением 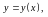криволинейный интеграл вычисляется по формуле: . (10.4)

Если линия АВ задана параметрическими уравнениями 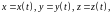то

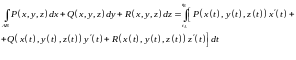(10.5)

Для плоского случая, если линия АВ задана параметрическими уравнениями 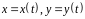, криволинейный интеграл вычисляется по формуле:

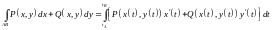, (10.6)

где - значения параметра t, соответствующие начальной и конечной точкам пути интегрирования.

Если линия АВ кусочно-гладкая, то следует воспользоваться свойством аддитивности криволинейного интеграла, разбив АВ на гладкие дуги.

Пример 10.1 Вычислим криволинейный интеграл 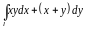вдоль контура, состоящего из части кривой 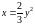от точки 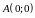до 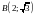и дуги эллипса 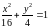от точки до .

Р

Рисунок 10.2

ешение. Построим заданный контур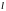 на плоскости в системе

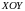
( см. рис. 10.2) Т

Рисунк 10.1

. к. контур состоит из двух частей, воспользуемся свойством аддитивности криволинейного интеграла: . Сведём оба интеграла к определённым. Часть контура задана уравнением относительно переменной 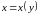. Воспользуемся формулой (10.4), в которой поменяем ролями переменные. Т.е.

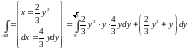. После вычисления получим .

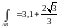Для вычисления интеграла по контуру ВС перейдём к параметрической форме записи уравнения эллипса и воспользуемся формулой (10.6).

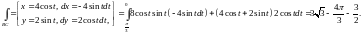Обратите внимание на пределы интегрирования. Точке 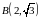соответствует значени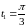е , а точке 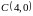соответствует 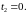Ответ: .

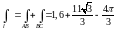Пример 10.2. Вычислим вдоль отрезка прямой АВ, где А(1,2,3), В(2,5,8).

Решение. Задан криволинейный интеграл 2-ого рода. Для вычисления необходимо преобразовать его в определённый. Составим уравнения прямой. Её направляющий вектор имеет координаты .

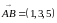Канонические уравнения прямой АВ: .

Параметрические уравнения этой прямой: ,

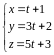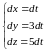
При .

Воспользуемся формулой (10.5):

.

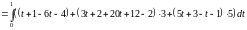Вычислив интеграл, получим ответ: .
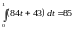