4. Ротор (вихрь) векторного поля. Формула Стокса.

Пусть - векторное поле, заданное в конечной области G с гладкой (или кусочно-гладкой) границей σ и 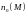- единичный вектор внешней нормали к σ в точке M. Вектор-функция

называется циркуляцией поля по границе области G.

Если существует предел при стягивании объёма V, заключённого внутри 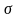в точку :

,

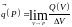то вектор 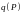называется ротором или вихрем поля в точке и обозначается символом 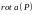. По определению:

.

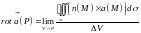это плотность циркуляции векторного поля по границе области.

Пусть в области G задано векторное поле и пусть M- внутренняя точка области G,π –некоторая плоскость, проходящая через эту точку. 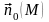- единичный вектор нормали к π, L- замкнутый контур, лежащий в плоскости и ограничивающий область Ф, такую, что M - внутренняя точка области Ф. Тогда принимают

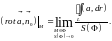
В правую часть формулы входят величины, инвариантные относительно выбора системы координат (циркуляция векторного поля вдоль замкнутого контура и площадь плоской области).

Если компоненты поля 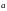имеют непрерывные частные производные по 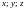, то вектор ротора поля вычисляется по формуле:

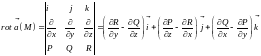. (15.8)

В частности, для плоского поля : .

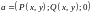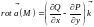Определение. Если в каждой точке области выполняется равенство 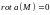, то поле называется безвихревым.

Теорема. В односвязной области всякое безвихревое поле потенциально.

.

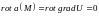Это является необходимым и достаточным условием потенциальности поля в поверхностно односвязной области. Если область не является поверхностно односвязной, то условие не достаточно для потенциальности поля.

Пусть в области G определено векторное поле 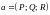, L – замкнутый контур, расположенный в области G, σ – поверхность, ограниченная гладким или кусочно-гладким контуром L, 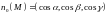- единичный вектор нормали на выбранной стороне поверхности σ. Пусть функции непрерывны вместе со своими частными производными. Тогда справедлива формула Стокса:

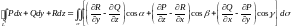. (15.9)

Ориентация контура L согласована с ориентацией поверхности σ по правилу правого винта. (См.рис. 15.4) Или:

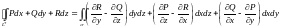. (15.10)

Л

Рисунок 15.4

евая часть формулы Стокса – это циркуляция векторного поля вдоль контура L, а правая представляет собой поток через поверхность σ векторного поля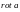 . Формулу Стокса можно записать в векторной форме: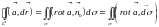 . (15.11)

Физический смысл формулы Стокса: циркуляция векторного поля вдоль замкнутого контура равна потоку ротора этого поля через произвольную поверхность, натянутую на этот контур.

Замечание. Формула Стокса остаётся справедливой и в случае,

когда поверхность σ является плоской областью, параллельной какой-нибудь координатной плоскости. Тогда формула Стокса превращается в формулу Грина:

.

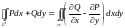Пример 15.3. Проверим, является ли потенциальным векторное поле .

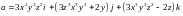Решение. По формуле (15.8) имеем:

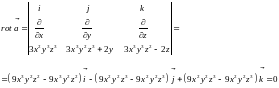
Ответ: данное поле является потенциальным, т.к. .

П ример 15.4. Вычислим циркуляцию векторного поля

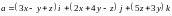
по контуру треугольника ABC , где A(1,1,0), B(0,0,2), C(3,0,1), двумя способами: 1) с помощью криволинейного интеграла, 2) по формуле Стокса.

Выясним, как зависит циркуляция от расположения контура в данном поле.

Рисунок 15.5

Решение.

1. Вычислим циркуляцию по формуле (15.3):

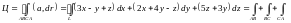(см. рис.15.5)

2. С

   Рисунок 13

   оставим уравнения прямых, содержащих стороны треугольника.

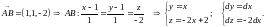
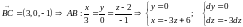
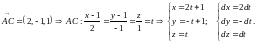
Вычислим криволинейные интегралы, преобразовав их в определённые.

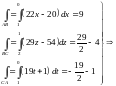Просуммировав, получим ответ:

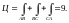
2) Проверим полученный ответ, вычислив циркуляцию по формуле Стокса: 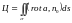. (см. (15.11)). В качестве поверхности σ, на которой располагается заданный контур, выберем плоскость треугольника ABC. Тогда 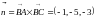. Единичный вектор нормали, составляющий острые углы с осями координат: .

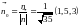Найдём по формуле (15.8) и скалярное произведение: , .

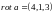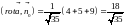Получим 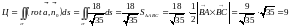, т.е. тот же ответ.

3) Исследуем поведение циркуляции при перемещении нашего контура в пространстве. Для этого используем определение скалярного произведения.

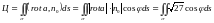, где 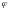– угол между векторами и .

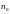Видим, что циркуляция зависит от этого угла . Отсюда следует, что если треугольник ABC перемещается в пространстве параллельно своему исходному положению, то угол не меняется, и циркуляция по контуру остаётся равной 9, а при повороте контура меняется направление вектора , что влечёт изменение циркуляции.

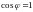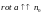Циркуляция достигнет максимального значения, когда , т.е. когда . В этом случае .

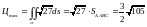Ответ: Ц=9, .

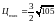Занятие 16.

Оператор Гамильтона. Повторные дифференциальные операции.

Ауд.: ОЛ-6 №№ 2382, 2385(б), 2398(б) или ОЛ-5 №№ 10.122, 126, 126, 127, 149 (а, в).