1.Криволинейный интеграл в векторном поле.

К

Рисунок 15.1

риволинейный интеграл векторного поля – это криволинейный интеграл второго рода. Определяется он следующим образом. Пусть в области G задано векторное поле и в этом поле определена гладкая или кусочно-гладкая ориентированная кривая АВ. Разобьём кривую АВ на n частей точками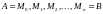 по направлению от А к В. (см. рис.15.1)Радиус-вектор точки 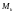обозначим 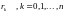. Вектор

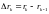. Выберем произвольно на каждой частичной дуге 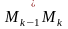точку 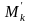и вычислим вектор поля 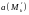в них. Для всех 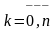вычислим значения скалярного произведения и составим интегральную сумму .

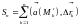Определение. Криволинейным интегралом векторного поля 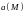вдоль дуги АВ называется предел (если он существует), к которому стремится интегральная сумма 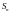, если наибольшая из длин частичных дуг 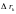стремится к нулю, а число элементарных дуг n неограниченно возрастает. Этот предел обозначают символом 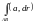. Т.е.

. (15.1)

При изменении ориентации кривой интеграл меняет знак: .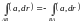

Физический смысл выражения - это работа, произведённая силой при перемещении материальной точки от А к В по линии L.

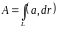(15.2)

Криволинейный интеграл векторного поля вдоль замкнутой кривой (контура L) называется циркуляцией поля по замкнутому контуру при заданном направлении обхода контура и обозначается символом

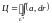(15.3)

(знак + обозначает, что контур обходится против часовой стрелки).

Пусть поле задано своими функциями-координатами и 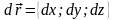. Тогда

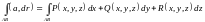. (15.4)

В правой части выражения (15.4)- криволинейный интеграл второго рода.

Для плоского поля 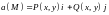криволинейный интеграл вычисляется по формуле: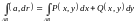 . (15.5)

Криволинейный интеграл векторного поля вычисляется по обычным правилам вычисления криволинейного интеграла второго рода, т.е. преобразовывается в определённый. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование. (См. занятие 10)

Пример 15.1. Найдём работу векторного поля 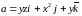при перемещении точки вдоль меньшей части кривой, являющейся пересечением цилиндра 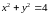и параболоида гиперболического 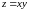, от точки 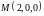к .

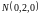Решение. Построим заданную часть кривой (см. рис. 15.2) и вычислим работу по формуле (15.2):

.

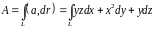Построенный криволинейный интеграл 2-ого рода сведём к определённому.

Д ля этого используем параметрическую форму записи уравнений кривой 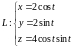, где .

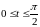Тогда работа

Рисунок 15.2

.

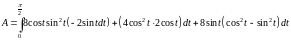После вычисления получаем ответ: .

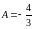2. Потенциальное векторное поле.

Определение . Векторное поле называется потенциальным в области G, если существует такая скалярная функция 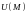, что её градиент равен вектору , т.е. .

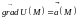Функция 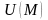называется скалярным потенциалом векторного поля . Если , то из определения следует, что

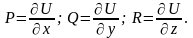
Пусть функции 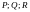имеют непрерывные частные производные в односвязной области G. Тогда для потенциального поля можно доказать эквивалентность следующих утверждений.

1) Поле является потенциальным тогда и только тогда, когда (15.6)

Для плоского 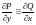поля: . Это необходимые и достаточные условия потенциальности поля.

2) Циркуляция потенциального векторного поля по любому замкнутому контуру 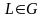равна нулю.

3) В области 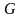существует скалярная функция 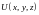, полный дифференциал которой совпадает с подынтегральным выражением 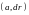криволинейного интеграла, т. е. 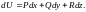В этом случае функция определяется не однозначно, а с точностью до постоянного слагаемого, т.к.

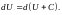
4) Криволинейный интеграл потенциального векторного поля не зависит от пути, соединяющего две произвольные точк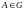и и 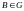, а зависит только от положения этих точек. Имеет место формула Ньютона-Лейбница.

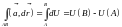, (15.7)

т.е. работа в потенциальном поле не зависит от выбора пути между точками А и В, и равна разности потенциалов в этих точках.

Пример 15.2. Убедимся в том, что поле

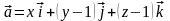
я

Рисунок 12

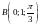вляется потенциальным, найдём потенциал поля U и вычислим работу, совершаемую этим полем при перемещении материальной точки из в .

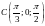Решение. Поле определено в каждой точка пространства . Проверим потенциальность поля (см. (15.6)):

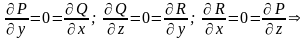условия выполнены, поле потенциально.

Рисунок 15.3

Для вычисления потенциала воспользуемся тем, что линейный интеграл в таком поле не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка 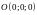- начало пути, а некоторая точка 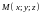- конец пути. Вычислим интеграл 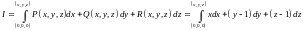по контуру, состоящему из отрезков прямых, параллельных координатным осям (см.Рисунок 12). .

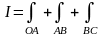Уравнения частей контура: , , .

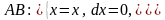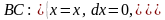Тогда , .

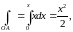
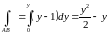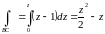В итоге получаем: .

Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница: .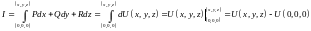

Сравним результаты: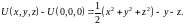

Из полученного равенства следует, что 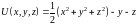, а 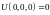. Потенциал данного поля 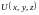найден.

Найдём работу, совершаемую векторным полем при перемещении точки из 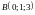в 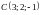. В потенциальном поле работа равна разности потенциалов в конечной и начальной точках пути (см.(15.7)), т. е. 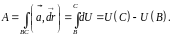Вычислив значения потенциал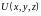а в точках, получаем ответ: работа .