
- •Б.Т. Добрица, и.В. Дубограй, о.В. Скуднева. Криволинейные, поверхностные интегралы и элементы теории поля.
- •1.Определение криволинейного интеграла 1-ого рода.
- •2.Свойства криволинейного интеграла 1 рода.
- •3.Способы вычисления криволинейного интеграла 1 рода.
- •4.Теорема существования криволинейного интеграла 1 рода.
- •5.Физические приложения криволинейного интеграла первого рода.
- •6.Примеры решения задач.
- •1.Определение криволинейного интеграла второго рода.
- •2.Теорема существования криволинейного интеграла 2-ого рода.
- •4.Вычисление криволинейного интеграла 2-ого рода.
- •5. Работа силы при перемещении материальной точки единичной массы из точки в точку вдоль кривой .
- •1.Формула Грина.
- •2. Независимость криволинейного интеграла от пути интегрирования.
- •Определение поверхностного интеграла первого рода.
- •2.Вычисление поверхностного интеграла 1-ого рода.
- •5.Примеры решения задач.
- •1.Понятие гладкой поверхности. Ориентированная поверхность.
- •2.Определение поверхностного интеграла второго рода.
- •3.Вычисление поверхностного интеграла 2-ого рода.
- •1.Векторное поле.
- •2. Векторные линии поля.
- •3.Поток векторного поля через поверхность.
- •4.Дивергенция векторного поля. Соленоидальное векторное поле.
- •Формула Остроградского – Гаусса.
- •1.Криволинейный интеграл в векторном поле.
- •2. Потенциальное векторное поле.
- •4. Ротор (вихрь) векторного поля. Формула Стокса.
- •1.Оператор Гамильтона.
- •2.Дифференциальные операции первого порядка.
- •2.Дифференциальные операции второго порядка.
- •4.Запись дифференциальных операций второго порядка в операторной форме.
Московский государственный технический университет
имени Н.Э. Баумана
Факультет «Фундаментальные науки»
Кафедра «Математическая физика и вычислительная математика»
Б.Т. Добрица, и.В. Дубограй, о.В. Скуднева. Криволинейные, поверхностные интегралы и элементы теории поля.
методическое пособие к практическим занятиям.
Москва
Занятие 9.
Криволинейный
интеграл 1-го рода: определение, основные
свойства, вычисление с помощью
определенного интеграла. Формулировка
теоремы существования криволинейного
интеграла первого рода, независимость
вычисления от направления обхода
кривой. Физические
приложения криволинейного интеграла
первого рода: масса кривой, статистические
моменты кривой относительно осей
 и
и
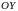 ;
моменты инерции кривой.
ОЛ-1 гл.5,
ОЛ-2 гл.2, ОЛ-4 гл.3
§ 9
;
моменты инерции кривой.
ОЛ-1 гл.5,
ОЛ-2 гл.2, ОЛ-4 гл.3
§ 9
Практика: ОЛ-6 №№ 2293, 2295, 2296, 2299, 2306, 2307 или ОЛ-5 №№
1.Определение криволинейного интеграла 1-ого рода.
Р
ок 9. 1
Рисунок 9.2

Рисунок 9.3
ассмотрим кусочно-гладкую кривую ,
в каждой точке М
которой задана функция
,
в каждой точке М
которой задана функция
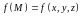 .
Разобьём эту кривую на
.
Разобьём эту кривую на
 малых частей точками
малых частей точками
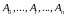 так, чтобы в точках каждой части
так, чтобы в точках каждой части
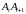 значение функции
значение функции
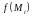 можно
было считать постоянным, а сама часть
могла быть принята за отрезок прямой
(см. рис. 9.1). Пусть
можно
было считать постоянным, а сама часть
могла быть принята за отрезок прямой
(см. рис. 9.1). Пусть
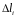 - длина i-ой части разбиения. На каждой
части выберем произвольную точку
- длина i-ой части разбиения. На каждой
части выберем произвольную точку
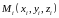 и
и
составим
интегральную сумму
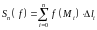 .
Определение.
Криволинейным интегралом первого рода
называется предел интегральной суммы
(если он существует) при неограниченном
увеличении числа разбиений и стремлении
длины каждой части к нулю.
.
Определение.
Криволинейным интегралом первого рода
называется предел интегральной суммы
(если он существует) при неограниченном
увеличении числа разбиений и стремлении
длины каждой части к нулю.
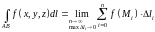 .
(9.1)
.
(9.1)
2.Свойства криволинейного интеграла 1 рода.
1.Независимость значения криволинейного интеграла первого рода от направления движения точки по кривой:
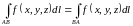 (9.2)
(9.2)
2.Свойство линейность криволинейного интеграла:
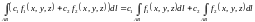 (9.3)
(9.3)
3. Свойство аддитивности:
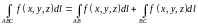 (9.4)
(9.4)
4.
Свойство
монотонности.
Если
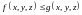 на кривой АВ,
то
на кривой АВ,
то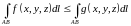 (9.5)
(9.5)
5.
Теорема о
среднем.
Если
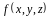 непрерывна
на кривой АВ,
то существует
число ζ такое, что
непрерывна
на кривой АВ,
то существует
число ζ такое, что
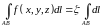 (9.6)
(9.6)
6. Криволинейный интеграл от единичной функции равен длине кривой:
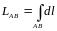 (9.7)
(9.7)
3.Способы вычисления криволинейного интеграла 1 рода.
1.Если
кривая задана в пространстве как
пересечение двух поверхностей
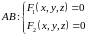 ,
то можно выразить из системы уравнений
этих поверхностей две переменные через
третью, например,
,
то можно выразить из системы уравнений
этих поверхностей две переменные через
третью, например,
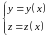 .
Тогда длина отрезка прямой
.
Тогда длина отрезка прямой
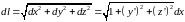 и
и
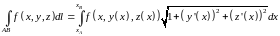 .
(9.8)
.
(9.8)
2.Если
кривая задана параметрически
уравнениями: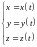 ,
то длина отрезка прямой
,
то длина отрезка прямой
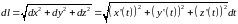 ,
и
,
и
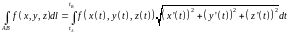 (9.9)
(9.9)
3.Если
задана плоская кривая и в каждой её
точке определена функция
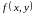 ,
то формулы (9.8) и (9.9) упрощаются:
,
то формулы (9.8) и (9.9) упрощаются:
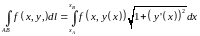 ,
(9.8а)
,
(9.8а)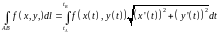 .
(9.9а)
.
(9.9а)
4.Если
на плоскости кривая задана в полярной
системе уравнением
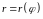 ,
то
,
то
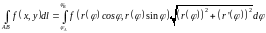 (9.10)
(9.10)
Примечание.
а) Если контур интегрирования – отрезок
прямой, соединяющий точки
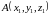 и
и
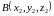 ,
то уравнения этого контура имеют вид
,
то уравнения этого контура имеют вид
 .
б) Если контуром интегрирования
является эллипс
.
б) Если контуром интегрирования
является эллипс
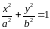 ,
то удобно перейти к параметрическому
заданию этой кривой, где
,
то удобно перейти к параметрическому
заданию этой кривой, где
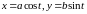 (частный случай – окружность с
(частный случай – окружность с
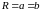 ).
).
