Минимизация функций с использованием карт Карно

Отличие карт Карно от карт Вейча заключается в способе обозначе­ния строк и столбцов таблицы истинности. Таблица иллюстрирует карты Карно для функций трех и четырех аргументов.

Аргументы функции делятся на две группы, комбинации значений аргументов одной группы приписываются столбцам таблицы, комбина­ции значений аргументов другой группы — строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующими последова­тельности чисел в коде Грея (это сделано для того, чтобы склеивающиеся клетки находились рядом). Обозначения столбца и строки, на пересече­нии которых находится клетка таблицы, образуют набор, значение функции на этом наборе записывается в клетку.

00

01

11

10

00

01

11

10

0

F(000)

F(010)

F(110)

F(100)

00

F(0000)

F(0100)

F(1100)

F(1000)

1

F(001)

F(011)

F(111)

F(101)

01

F(0001)

F(0101)

F(1101)

F(1001)

11

F(0011)

F(0111)

F(1111)

F(1011)

10

F(0010)

F(0110)

F(1110)

F(1010)

		00	01	11	10								00	01	11	10
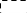
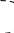	00	0	0	1	1							0 0	1	0	0	1
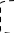
	01	1	1	0	0							01	1	1	1	1
	11	1	1	0	0							11	0	0	1	1
	10	0	0	0	0							10	0	0	1	1

Для получения МДНФ функции охватываются областями клетки таблицы, содержащие 1. Как и в случае минимизации с помощью карт Вейча, области должны быть прямоугольной формы и содержать 2ⁿ клеток (при целочисленном значении n). Для каждой области составля­ется набор из двух комбинаций: приписанных столбцам и приписанных строкам, на пересечении которых расположена область. При этом если области соответствуют несколько комбинаций кода Грея, приписанных столбцам или строкам, то при составлении набора области записывает­ся общая часть этих комбинаций, а на месте различающихся разрядов комбинаций ставятся звездочки. 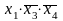Например, для функции, представлен­ной табл., области I будет соответствовать набор 1*00 или член МДНФ , области II—набор 0**1 или член МДНФ 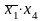.Таким образом, для этой функции МДНФ

Для получения МКНФ областями охватываются клетки, содержа­щие 0, и члены МКНФ записываются через инверсии цифр, получаемых для наборов отдельных областей. Так, для функции, представленной в табл. 1.35, области I соответствует набор * 100 и член МКНФ 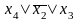, области II — набор 0* 1 * и член 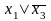. Таким образом, МКНФ функции

Общие правила минимизации с использованием карт Карно-Вейча

1. В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания или нахождения импликант данной функции.

2. Количество клеток внути контура должно быть целой степенью двойки (1, 2, 4, 8, 16...).

3. При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).

4. Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.

5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.

6. Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ). Целью минимизации является нахождение минимальной из множества тупиковых форм.

7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура. Переменные булевой функции входят в элементарную коньюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией - если 0. Для значений булевой функции, равных 0, записываются элементарные дизьюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией - если 1.