Практическая работа № 8
Тема: «ВЫПОЛНЕНИЕ МИНИМИЗАЦИИ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ МЕТОДАМИ КВАЙНА И КВАЙНА-МАК-КЛАСКИ»
ЦЕЛЬ:
Повторить –
законы алгебры логики;
построение таблиц истинности ФАЛ;
алгоритм нахождения СДНФ и СКНФ;
минимизацию ФАЛ методом непосредственных преобразований.
Научиться минимизировать логическую функции:
методом Квайна;
методом Квайна-МакКласки.
Краткие теоретические сведения Повторим минимизацию логических функций методом карт Карно-Вейча
Некоторые выражения, составленные по только что сформулированной теореме, можно упростить, применяя аксиомы и законы булевой алгебры. Дело это несложное, но требует аккуратности и внимания, а допущенная при процедуре упрощения неточность приводит к ошибочному результату. Чтобы исключить подобного рода неточности и избавиться от однообразной и малоинтересной работы, упрощения выражений производят при помощи диаграмм (карт) минимизации.
Диаграммы минимизации содержат 2n клеточек, каждая из которых предназначена для одной из простых конъюнкций или, что то же самое, для одного набора значений переменных. В случае n = 2 диаграмма для минимизации совпадает с принятой формой представления таблицы значений функции двух переменных. В этой диаграмме любые соседние клетки отличаются лишь появлением или исчезновением знака инверсии над одной переменной, а соответствующие им наборы переменных отличаются лишь одной цифрой. Этот же принцип сохраняется и при большем количестве переменных.
Для n = 3 диаграмма строится путем пририсовки к диаграмме для двух переменных ее зеркального изображения (рис. 1.). Всем клеточкам «старой» части ставится в соответствие новая переменная, равная 0, «пририсованной» — равная 1. Таким же способом строят диаграммы для любого количества переменных, например для n = 4 (рис. 2.).
N=2 N=3 N=4
-
0
1
00
01
11
10
00
01
11
10
0
0
00
1
1
01
11
0
1
00
01
11
10
10
0
00
01
0
000
001
011
010
1
10
11
1
100
101
111
110
00
01
11
10
00
0
1
3
2
0
1
00
01
11
10
0
0
1
0
0
1
3
2
01
4
5
7
6
1
2
3
1
4
5
7
6
11
12
13
15
14
10
8
9
11
10
Рис.1
Используя диаграммы, нет необходимости записывать булево выражение искомой комбинационной схемы. Достаточно лишь занести 1 в клеточки, соответствующие наборам переменных, при которых на выходе комбинационной схемы должен быть сигнал 1 (вспомните «крестики-нолики»!).
Если занесенные единицы образуют прямоугольник из 2n клеточек, то логическая сумма соответствующих им простых конъюнкций может быть заменена укороченной конъюнкцией, содержащей лишь те переменные, значения которых одинаковы для всех клеточек данного прямоугольника. Для этого такие массивы из 2, 4, 8 и т. д. клеточек обводятся контурами. Искомое минимизированное булево выражение есть сумма конъюнкций контуров, охватывающих все без исключения единицы. При этом крайние правый и левый столбцы диаграммы и верхняя и нижняя ее строки считаются соседними, а контуры могут перекрываться. Чем объясняется такая процедура минимизации, поясним на примере выражения. Сначала упростим его обычным методом, используя законы алгебры логики: з-н коммутативности, з-н поглощения, з-н дистрибутивности.
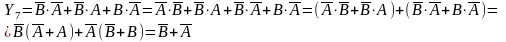
Теперь
проделаем то же самое, используя диаграмму
минимизации для двух переменных (табл.
1). Укороченная конъюнкция, получающаяся
в результате оконтуривания клеточек
и
,
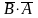есть просто
,
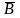а укороченная конъюнкция
от контура с клеточками
и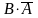
есть просто
.
Таким образом, сразу
же можно записать
,
что совпадает с формулой. Приведем еще
два примера составления и минимизации
выражений, описывающих действие схем,
заданных таблицами значений:
-
0
1
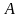
0
1
1
и
1
1
1
1
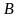
1
-
№
C
B
A
Y
0
0
0
0
1
1
0
0
1
0
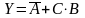
2
0
1
0
1
BC
3
0
1
1
0
C
00
01
11
1
04
1
0
0
1
0
1
1
5
1
0
1
0
6
1
1
0
1
1
1
1
1
7
1
1
1
1
-
№
C
B
A
D
Y
0
0
0
0
0
0
1
0
0
0
1
0
2
0
0
1
0
0
3
0
0
1
1
1
4
0
1
0
0
1
5
0
1
0
1
1
6
0
1
1
0
1
BA
7
0
1
1
1
1
DC
00
01
11
10
8
1
0
0
0
0
00
1
1
9
1
0
0
1
1
10
1
0
1
0
1
01
1
1
1
1
11
1
0
1
1
1
12
1
1
0
0
0
11
1
1
13
1
1
0
1
1
14
1
1
1
0
0
10
1
1
1
15
1
1
1
1
1
Рис.2.