РОЗДІЛ IV

ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ

ОДНІЄЇ ЗМІННОЇ

Похідною функції по фрагменту називають границю відношення приросту функції до приросту аргументу, коли приріст аргумента прямує до нуля і позначають: , , , , тобто

4.1. ОСНОВНІ ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ

, де

1. 

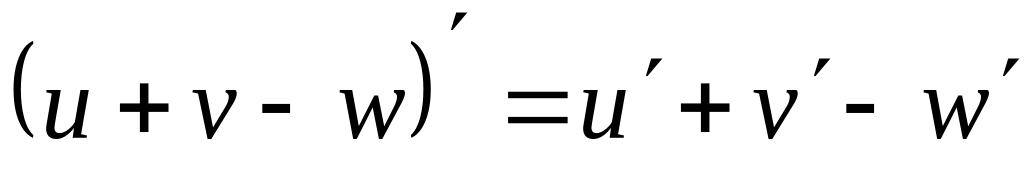
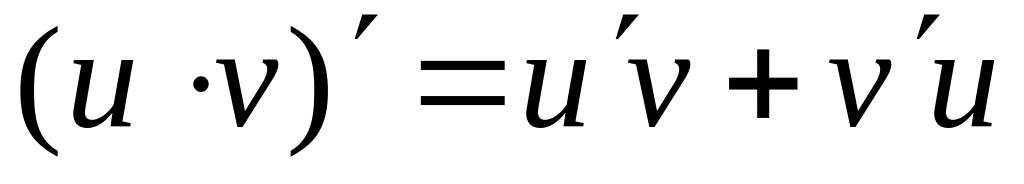2. наслідок: 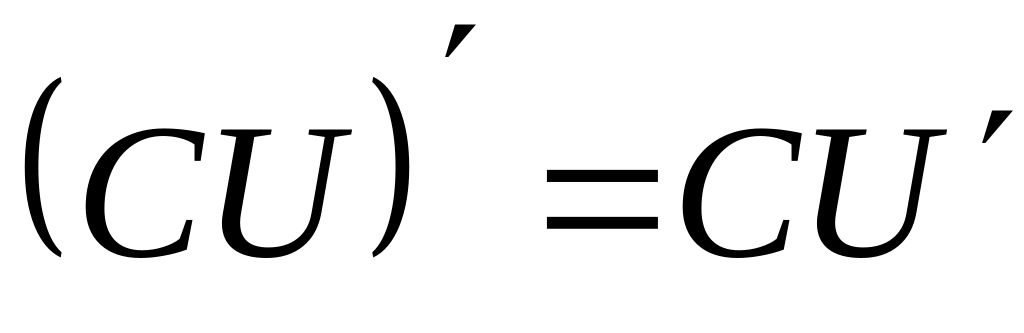, де

3. .

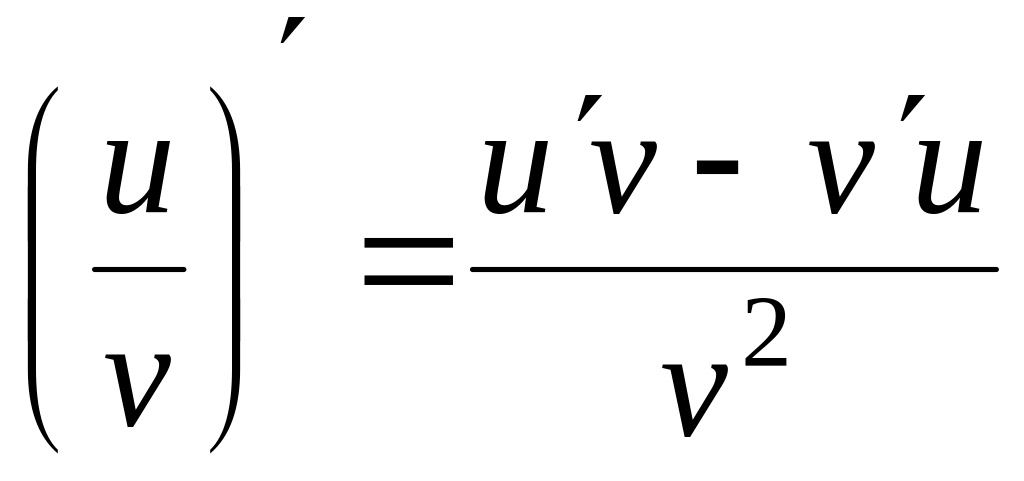4.2. ПОХІДНА СКЛАДНОЇ ФУНКЦІЇ

Нехай , а , тоді складна функція. В цьому випадку

4.3. ТАБЛИЦЯ ПОХІДНИХ

1)	6)
2)	7)
2')	8)
3)	9)
3')	10)
4)	11)
5)

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ

Знайти похідні функцій:

Приклад 1.

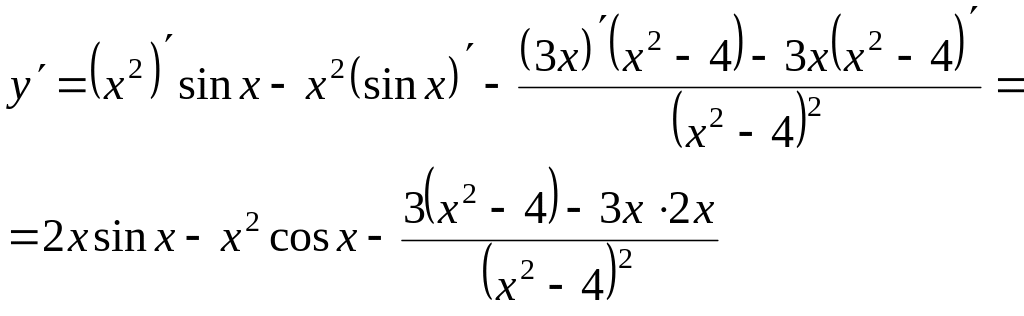
Приклад 2.

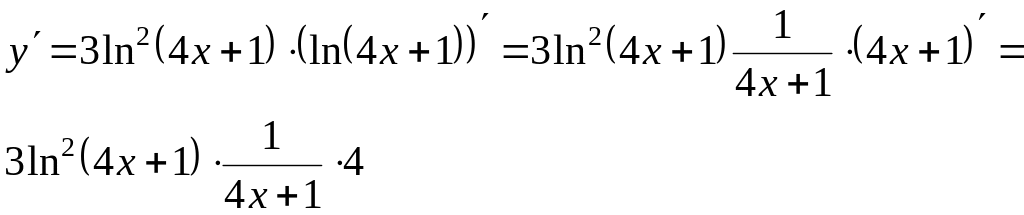
Приклад 3

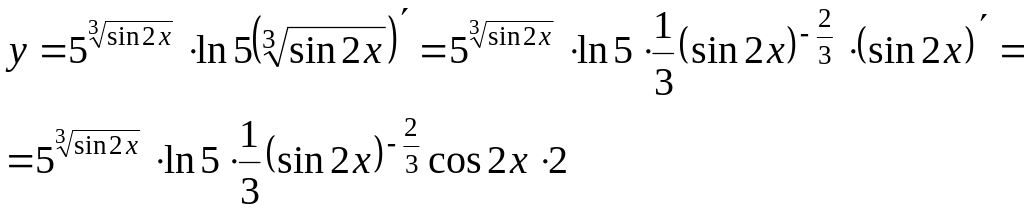
4.4. ПОХІДНА НЕЯВНО ЗАДАНОЇ ФУНКЦІЇ

Нехай змінні та зв’язані між собою деяким рівнянням , тобто функція задано неявно. Для того щоб знайти похідну неявно заданої функції необхідно знайти похідну від лівої і правої частини по , враховуючи, що є функцією , а потім виразити . Розглянемо це на прикладі:

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ

Приклад 1.

. Знайти :

1)

2)

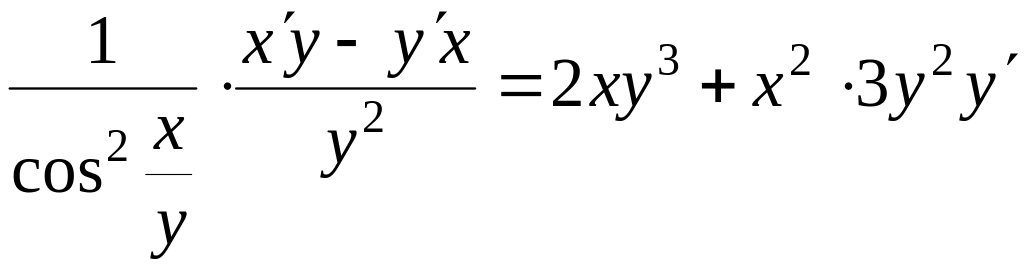
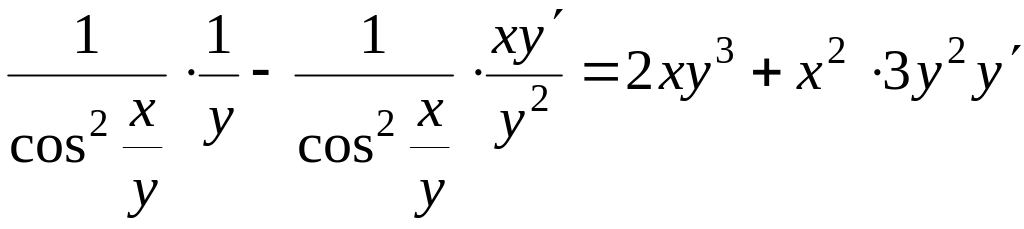
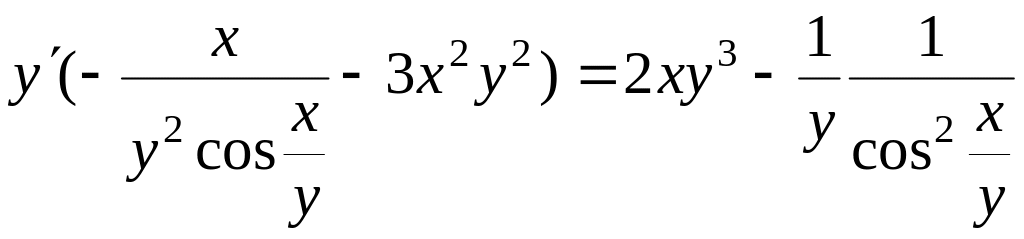
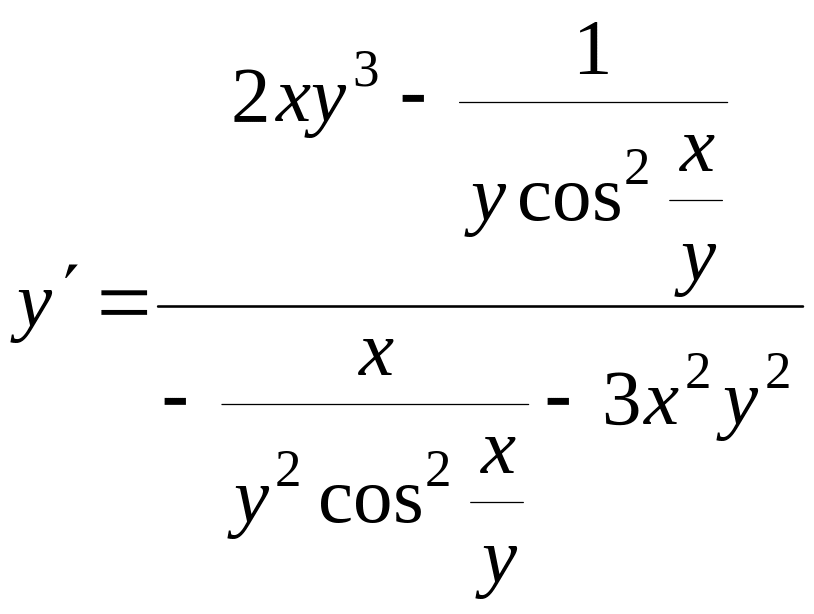
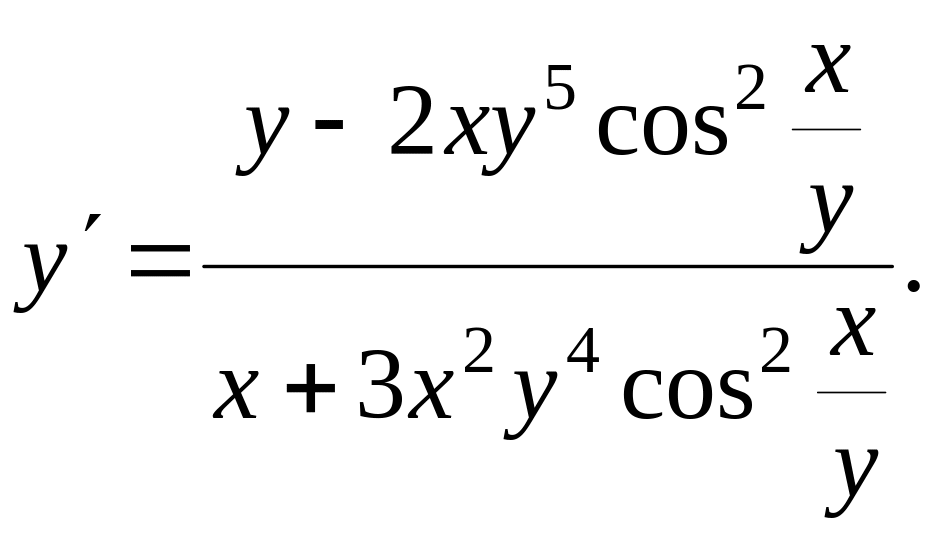
4.5. ПОХІДНІ ВИЩИХ ПОРЯДКІВ

Похідну від першої похідної називають похідною другого порядку або другою похідною і позначають .

Похідною го порядку від функції називають похідну від похідної го порядку і позначають .

4.6. ДИФЕРЕНЦІАЛ ФУНКЦІЇ

Диференціалом функції називають величину пропорційну нескінченно малому приросту аргумента , яка відрізняється від відповідного приросту функції на нескінченно малу величину більш високого порядку, ніж .

Таким чином, якщо функція має похідну , то добуток цієї похідної на і є диференціалом функції: .

Властивості диференціалу:

1) ;

2) ;

3) ;

4) .

4.7. Правило лопіталя

Нехай та - дві неперервні на відрізку і диференційовані всередині нього функції, причому не перетворюється в нуль всередині відрізка і нехай , тобто перетворюється на нуль при . Тоді, якщо існує границя відношення при , то існує і границя відношення при , причому .

Наслідки:

1) Якщо і задовольняють тим же умовам, які накладались на і , то

.

2) Теорема має місце і в тому випадку, коли і не визначені при , але

і .

3) правило Лопіталя можна застосовувати і в тому випадку, коли

і

Приклади розв'язування задач

Приклад 1.

За правилом Лопіталя знайти границі.

а)

б)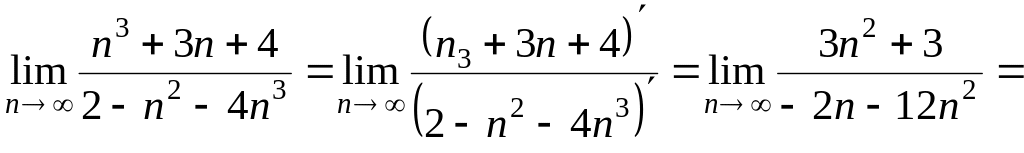

в)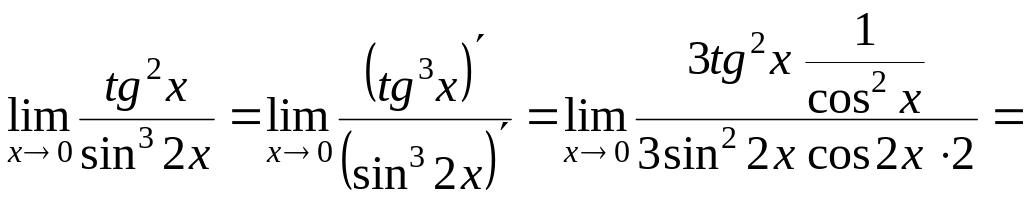

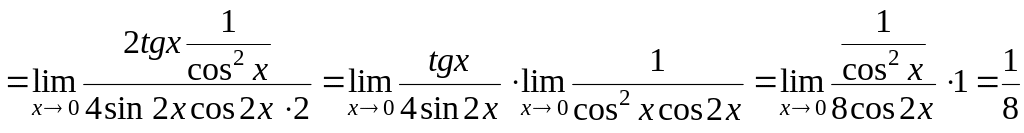
4.8. Дослідження функції

Достатня умова зростання функції.

Якщо функція неперервна на відрізку і диференційована на інтервалі , при цьому для будь-яких , то функція зростає на .

Достатня умова спадання функції.

Якщо функція неперервна на відрізку і диференційована на інтервалі , при цьому для всіх , то функція спадає на відрізку

Функція в т. має мінімум, якщо значення функції в цій точці менша ніж значення функції в деякому околі цієї точки.

Функція в т. має максимум, якщо значення функції в цій точці більше ніж значення функції в деякому околі цієї точки.

Точки максимуму та мінімуму називають точками екстремуму функції.

Точки, в яких перша похідна дорівнює нулю або не існує називають критичними точками.

Достатня умова існування екстремуму.

Нехай функція неперервна на деякому інтервалі, який містить критичну точку , і диференційована в усіх точках цього інтервалу за винятком, можливо, самої точки . Тоді

1) якщо при переході зліва на право через точку перша похідна змінює знак «+» на «-», то в цій точці функція має максимум;

2) якщо при переході зліва на право через точку перша похідна змінює знак «-» на «+», то в цій точці функція має мінімум;

3) якщо при переході через точку похідна не змінює знаку, то в даній точці екстремуму не має.

Опуклості та вгнутість кривої.

Криву називають вгнутою (або повернутою опуклістю вниз) на інтервалі , якщо всі точки кривої лежать вище будь-якої її дотичної на цьому інтервалі.

Криву називають опуклою (або повернутою опуклістю вгору) на інтервалі , якщо всі точки кривої лежать нижче ніж будь-яка її дотична на цьому інтервалі.

Точки, які відділяють вгнуту частину кривої від опуклої називають точками перетину.

Умова опуклості функції.

Якщо в усіх точках інтервалу друга похідна функції від’ємна , то крива на цьому інтервалі опукла.

Умова вгнутості функції.

Якщо в усіх точках інтервалу друга похідна функції додатня, то крива на цьому інтервалі вгнута.

Достатня умова існування точок перегину.

Нехай неперервна в точці крива визначена рівнянням . Якщо , або не існує, а при переході через точку похідна змінює знак, то точка кривої із абсцисою є точкою перегину.

Асимптоти кривої.

Пряму називають асимптотою кривої, якщо відстань від змінної точки кривої до даної прямої при віддаленні точки в нескінченність прямує до нуля.

Асимптоту, паралельну осі ординат називають вертикальною.

Щоб знайти вертикальну асимптоту, необхідно знайти таке значення , для якого буде виконуватися одна із рівностей

; ;

; .

Тоді буде вертикальною асимптотою.

Похилою асимптотою будемо називати асимптоту не паралельну осі ординат. Шукають похилі асимптоти у вигляді

.

Для відшукання коефіцієнтів і необхідно обчислити границі

, .

Визначивши , можна знайти із відповідних рівностей.

та

Загальна схема дослідження функції.

1) знаходимо область визначення функції;

2) знаходимо точки перетину графіка функції з осями координат;

3) знаходимо інтервали зростання та спадання функції, а також точки максиму та мінімуму функції;

4) знаходимо інтервали опуклості та вгнутості графіка, а також точки перетину;

5) знаходимо вертикальні та похилі асимптоти;

6) за одержаними результатами будуємо графік функції.